Channel Flow Basic Concepts, Equations, and Solution Techniques

Fundamental Equations of Open-Channel Flow

At the heart of the routing models included in the program are the fundamental equations of open channel flow: the momentum equation and the continuity equation. Together the two equations are known as the St. Venant equations or the dynamic wave equations. The momentum equation accounts for forces that act on a body of water in an open channel. In simple terms, it equates the sum of gravitational force, pressure force, and friction force to the product of fluid mass and acceleration. In one dimension, the equation is written as:

1)	$\begin{array}{l}\displaystyle S_{f}=S_{0}-\frac{\partial y}{\partial x}-\frac{V}{g} \frac{\partial V}{\partial x}-\frac{1}{g} \frac{\partial V}{\partial t}\end{array}$

where $\begin{array}{l}S_f\end{array}$ = energy gradient (also known as the friction slope); $\begin{array}{l}S_0\end{array}$ = bottom slope; V = velocity; y = hydraulic depth; x = distance along the flow path; t = time; g = acceleration due to gravity; $\begin{array}{l}\partial y/\partial x\end{array}$ = pressure gradient; (V/g) $\begin{array}{l}\partial V/\partial x\end{array}$ = convective acceleration; and (1/g)( $\begin{array}{l}\partial V/\partial t\end{array}$ ) = local acceleration.

The continuity equation accounts for the volume of water in a reach of an open channel, including that flowing into the reach, that flowing out of the reach, and that stored in the reach. In one-dimension, the equation is:

2)	$\begin{array}{l}\displaystyle A \frac{\partial V}{\partial x}+V B \frac{\partial y}{\partial x}+B \frac{\partial y}{\partial t}=q\end{array}$

where B = water surface width; and q = lateral inflow per unit length of channel. Each of the terms in this equation describes inflow to, outflow from, or storage in a reach of channel, a lake or pond, or a reservoir.

Henderson (1966) described the terms as A( $\begin{array}{l}\partial V/\partial x\end{array}$ ) = prism storage; VB( $\begin{array}{l}\partial y/\partial x\end{array}$ ) = wedge storage; and B( $\begin{array}{l}\partial y/\partial t\end{array}$ ) = rate of rise.
The momentum and continuity equations are derived from basic principles, assuming:

Velocity is constant, and the water surface is horizontal across any channel section.
All flow is gradually varied, with hydrostatic pressure prevailing at all points in the flow. Thus vertical accelerations can be neglected.
No lateral, secondary circulation occurs.
Channel boundaries are fixed; erosion and deposition do not alter the shape of a channel cross section.

Water is of uniform density, and resistance to flow can be described by empirical formulas, such as Manning's and Chezy's equation.

Approximations

Although the solution of the full equations is appropriate for all one-dimensional channel-flow problems, and necessary for many, approximations of the full equations are adequate for typical flood routing needs. These approximations typically combine the continuity equation (Equation 2) with a simplified momentum equation that includes only relevant and significant terms. Henderson (1966) illustrates this with an example for a steep alluvial stream with an inflow hydrograph in which the flow increased from 10,000 cfs to 150,000 cfs and decreased again to 10,000 cfs within 24 hours. The following table shows the terms of the momentum equation and the approximate magnitudes that he found. The force associated with the stream bed slope is the most important. If the other terms are omitted from the momentum equation, any error in solution is likely to be insignificant. Thus, for this case, the following simplification of the momentum equation may be used:

3)	$\begin{array}{l}\displaystyle S_{f}=S_{0}\end{array}$

If this simplified momentum equation is combined with the continuity equation, the result is the kinematic wave approximation, which is described here: Kinematic Wave Channel Routing Model.

Flow Component	Recession Constant, Daily
S_o (bottom slope)	26
$\begin{array}{l}\frac{\partial y}{\partial x}\end{array}$ (pressure gradient)	0.5
$\begin{array}{l}\frac{V}{g} \frac{\partial V}{\partial X}\end{array}$ (convective acceleration)	0.12 – 0.25
$\begin{array}{l}\frac{1}{g} \frac{\partial V}{\partial t}\end{array}$ (local acceleration)	0.05

Other common approximations of the momentum equation include:

Diffusion wave approximation. This approximation is the basis of the Muskingum-Cunge routing model, which is described here: Muskingum-Cunge Model.

4)	$\begin{array}{l}\displaystyle S_{f}=S_{0}-\frac{\partial y}{\partial x}\end{array}$

Quasi-steady dynamic-wave approximation. This approximation is often used for water-surface profile computations along a channel reach, given a steady flow. It is incorporated in HEC-RAS (USACE, 2023).

5)	$\begin{array}{l}\displaystyle S_{f}=S_{0}-\frac{\partial y}{\partial x}-\frac{V}{g} \frac{\partial V}{\partial x}\end{array}$

Solution Schemes

In HEC-HMS, the various approximations of the continuity and momentum equations are solved using the finite difference method. In this method, finite difference equations are formulated from the original partial differential equations. For example, $\begin{array}{l}\partial V/\partial t\end{array}$ from the momentum equation is approximated as $\begin{array}{l}\Delta V/\Delta t\end{array}$ , a difference in velocity in successive time steps $\begin{array}{l}\Delta t\end{array}$ , and $\begin{array}{l}\partial V/\partial x\end{array}$ is approximated as $\begin{array}{l}\Delta V/\Delta x\end{array}$ , a difference in velocity at successive locations spaced at $\begin{array}{l}\Delta x\end{array}$ . Substituting these approximations into the partial differential equations yields a set of algebraic equations. Depending upon the manner in which the differences are computed, the algebraic equations may be solved with either an explicit or an implicit scheme. With an explicit scheme, the unknown values are found recursively for a constant time, moving from one location along the channel to another. The results of one computation are necessary for the next. With an implicit scheme, all the unknown values for a given time are found simultaneously.

Parameters, Initial Conditions, and Boundary Conditions

The basic information requirements for all routing models are:

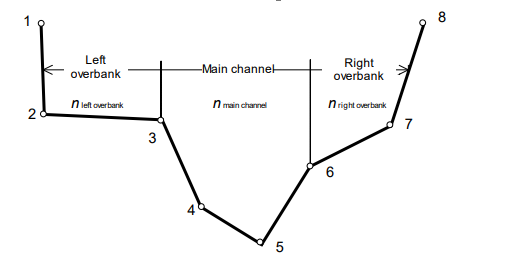
A description of the channel. All routing models that are included in the program require a description of the channel. In some of the models, this description is implicit in parameters of the model. In others, the description is provided in more common terms: channel width, bed slope, cross-section shape, or the equivalent. The 8-point cross-section configuration is one of the cross section shapes available to describe the channel. The 8 pairs of x, y (distance, elevation) values are described spatially in the figure below. Coordinates 3 and 6 represent the left and right banks of the channel, respectively. Coordinates 4 and 5 are located within the channel. Coordinates 1 and 2 represent the left overbank and coordinates 7 and 8 represent the right overbank.
Energy-loss model parameters. All routing models incorporate some type of energy-loss model. The physically-based routing models, such as the kinematic-wave model and the Muskingum-Cunge model use Manning's equation and Manning's roughness coefficients (n values). Other models represent the energy loss empirically.
Initial conditions. All routing models require initial conditions: the flow (or stage) at the downstream cross section of a channel prior to the first time period. For example, the initial downstream flow could be estimated as the initial inflow, the baseflow within the channel at the start of the simulation, or the downstream flow likely to occur during a hypothetical event.
Boundary conditions. The boundary conditions for routing models are the upstream inflow, lateral inflow, and tributary inflow hydrographs. These may be observed historical events, or they may be computed with the precipitation-runoff models included in the program.