Snowpack Mass and Energy Accounting

The two primary requirements of snowmelt hydrology are accounting for the time varying and spatially varying snowpack SWE and energy. The snowpack SWE is accounted for by balancing changes in SWE with the SWE deposited on or removed from the snow surface and the SWE lost from the snowpack as liquid water runoff. The snowpack energy is accounted for by balancing changes in the snowpack temperature and phase change with the heat flux at the snowpack top and bottom surfaces.

Snowpack Mass Balance

The snowpack mass balance describes changes in the snowpack SWE as a result of precipitation, runoff, sublimation, and blowing snow:

$\begin{array}{l}\displaystyle \frac{d\left(S W E_{t}\right)}{d t}=P_{t}-R_{t} \pm V_{t} \pm B_{t}\end{array}$

where SWE_t = the SWE of the snowpack (depth); t = time; P_t = the precipitation rate (depth/time); R_t = the runoff rate (depth/time); V_t = mass gained from or lost to water vapor (depth/time); and B_t = the snow gained from or lost to blowing snow (depth/time). (Variables with the subscript t are time varying.) The precipitation can be in the form of snow or rain – both will increase the SWE. The runoff rate (R_t) is determined by phase change in the snowpack which is determined through the energy balance calculations.

In general, the principal mass input into the snowpack is precipitation in the form of snow, which increases the snowpack SWE during the accumulation period; and the principal mass loss is liquid water runoff, which decreases the SWE during the ablation period. These are the processes modeled by the HEC-HMS Temperature Index Snow Model. However, mass lost to water vapor and blowing snow erosion and deposition can also be important at some locations.

Sublimation and condensation (V_t) describe the phase change of ice crystals of the snowpack directly into water vapor or the phase change of water vapor into ice or liquid water in the snowpack. Sublimation and condensation occur when heat is transferred between the snowpack and the atmosphere through the latent heat flux. (More about this in the heat transfer section below.) Blowing snow and sublimation can play significant roles in tundra, along alpine ridges, and other areas where strong winds and low humidity are common. In any case, sublimation, condensation, and blowing snow are not by the HEC-HMS Temperature Index Snow Model. As a result, the snowpack mass balance can be simplified to

$\begin{array}{l}\displaystyle \frac{d\left(S W E_{t}\right)}{d t}=P_{t}-R_{t}\end{array}$

Snowpack Energy Balance

The snowpack energy balance describes changes in the snowpack temperature and phase change in the snowpack as a result of heat transfer at the top and bottom surfaces of the snowpack. The snowpack energy balance is done per unit area of the snowpack surface. The snowpack is treated as a single layer with a uniform temperature. All heat transfer is vertical and there is no horizontal heat transfer within the snowpack.

If <0°C (32°F) the energy balance is

$\begin{array}{l}\displaystyle C_{p_{-} i e} \frac{d\left(\bar{\rho}_{s} D \bar{T}\right)}{d t}=Q_{\text {bta }}\end{array}$

where Q_total = the net heat flux at the snow surface (units of joules per second per unit area). (Q_total > 0, implies a net heat flow into the snowpack). Note that equation includes the snow depth and density inside the differentiation as the depth and density can also change with time. In general, the snow depth will only change with time under these conditions ( <0°C (32°F)) if there is snowfall occurring. This will be discussed in more detail below. Assume that the snow depth and density are constant with time as is usual under these conditions. Equation is then written as

$\begin{array}{l}\displaystyle C_{p_{-} i c e} \bar{\rho}_{s} D \frac{d \bar{T}}{d t}=C_{p_{-} i c e} \rho_{w} S W E \frac{d \bar{T}}{d t}=Q_{\text {total }}\end{array}$

Equation can be re-written in terms of the cold constant as

$\begin{array}{l}\displaystyle \frac{d C_{c}}{d t}=\frac{Q_{\text {total }}}{\rho_{w} \lambda}\end{array}$

where C_c = the Cold Content of the snowpack, as defined in equation . Note that equation and equation are entirely equivalent.

If =0°C (32°F), which is equivalent to C_c =0, and the net heat transfer is into the snowpack, that is, Q_total > 0, then the conditions are set for phase change, melting, to occur. The rate liquid water is formed from melting ice, M_t (depth/time), is

$\begin{array}{l}\displaystyle M_t = \frac{Q_{total}}{\rho_w \lambda}\end{array}$

If the ratio LWC/SWE $\begin{array}{l}\leq\end{array}$ LWC_max% then

$\begin{array}{l}\frac{d L W C}{d t}=M_{t} \\ R_{t}=0\end{array}$

If the percentage of the Liquid Water Content of the snowpack is less than LWC_max% then the liquid water created by melting snow increases the Liquid Water Content of the snowpack and no runoff occurs.

If LWC/SWE = $\begin{array}{l}LWC_{max\%}\end{array}$ then

$\begin{array}{l}R_{t}=M_{t} \\ \frac{d(S W E)}{d t}=-R_{t} \\ \frac{d L W C}{d t}=\frac{L W C_{\max \%}}{100 .} \frac{d S W E}{d t}\end{array}$

Once the percentage of the Liquid Water Content of the snowpack is equal to LWC_max% then all liquid water formed goes into runoff, which reduces the SWE and the LWC. This process can continue until the SWE is zero.

There are a number of different modes of heat transfer that are included in Q_total. These will be discussed next.

Snow Surface Heat Transfer

Overview

Snowmelt is ultimately driven by the transfer of heat energy into the snowpack from the atmosphere and the surrounding environment. There are four primary modes of heat transfer between the snowpack and its environment: sensible heat transfer, latent heat transfer, long wave radiation heat transfer, and short-wave radiation heat transfer. There is also heat transfer from precipitation falling on the snow surface as rain or snow, and heat transfer from the soil layer beneath the snowpack. This can be stated as

$\begin{array}{l}\displaystyle Q_{\text {total }}=Q_{\text {latent }}+Q_{\text {sensible }}+(1-\alpha) Q_{\mathrm{SW} \downarrow}+Q_{\mathrm{LWnet}}+Q_{\text {Precipitation }}+Q_{\text {Ground }}\end{array}$

where Q_Latent = the rate of latent heat transfer; Q_sensible = the rate of sensible heat transfer; Q_SW_â = the rate of downwelling shortwave radiation at the snow surface; α = the snowpack albedo (0< α <1); Q_LWnet = the rate of net longwave heat transfer; Q_{Precipitation} =the rate of heat transfer due to rain and snow falling on the snow surface; and Q_Ground = the rate of heat transfer from the ground beneath the snowpack.

It is important to note that HEC-HMS Temperature Index Snow Model does not model the individual modes of heat transfer included in equation explicitly. It uses a temperature index approach to simplify and model the net heat transfer instead. However, it is important to have insight into the physics of each mode of heat transfer. This is provided next.

Sensible and Latent Heat Transfer

Sensible and latent heat transfer are discussed together because both are driven by turbulent transport in the air between the snow surface and the lower part of the atmosphere. In fact, sensible and latent heat transfer are often referred to as turbulent fluxes due to the fact that they occur largely through turbulent transport in the air.

Sensible heat is the heat energy that can be measured with a thermometer. The direction of sensible heat transfer is always from the warmer object to the colder. So, for heat to be transferred into the snowpack from the atmosphere the air temperature must be warmer than the snowpack surface temperature. The heat transferred into the snowpack will cause the pack temperature to rise until the pack temperature reaches the equilibrium temperature of 0°C (32°F). Additional heat transfer into the snowpack after this point causes snowmelt. In similar fashion, for heat to be transferred from the snowpack into the atmosphere, the air temperature must be colder than the snowpack surface temperature. In this case, the snowpack temperature will drop. If the snowpack surface temperature and the air temperature are the same there will be no heat transfer between them as sensible heat.

Latent heat transfer is due to the transfer of water vapor between the snowpack surface and the atmosphere. Latent heat transfer always involves phases change between the water in the form of ice in the snowpack and the water in the form of vapor in the atmosphere. The transfer of water molecules directly from snow to vapor occurs by sublimation. Sublimation absorbs heat energy from the snowpack and cools it off. The transfer of water molecules directly from vapor to ice occurs by condensation (sometimes also referred to as deposition.) Condensation releases heat energy into the snowpack. The direction of latent heat transfer is determined by the difference between the water vapor pressure of the air immediately above the snowpack and the water vapor pressure in the atmosphere above the snowpack. The direction is from the higher vapor pressure layer to the lower vapor pressure layer. The water vapor pressure of the air immediately above the snowpack is the saturated vapor pressure at the temperature of the snow surface. Saturated vapor pressure is largely determined by air temperature and to a much less degree the atmospheric air pressure. Saturated vapor pressure means that the water contained in the air is in equilibrium with the ice of the snowpack and is the maximum amount of water that can be contained in the air at that temperature and atmospheric pressure immediately above ice. The vapor pressure of the atmosphere above the snowpack is determined by the relative humidity of the air and the air temperature.

The latent heat flux is from the air into the snowpack (condensation occurs) when

$\begin{array}{l}\displaystyle e_a > e_{sat(T_{ss})}\end{array}$

where e_a = the vapor pressure of the air; and e_sat(Tss)= the saturated vapor pressure immediately above the snow surface at the snow surface temperature, T_ss. The equation can be cast in terms of the relative humidity of the air (which is often known) by noting that the definition of relative humidity, RH,

$\begin{array}{l}\displaystyle RH = 100\frac{e_a}{e_{sat(T_a)}}\end{array}$

where e_sat(Ta)= the saturation vapor pressure of the air at the air temperature T_a. Substituting this into the previous equation, it can be seen that the latent heat transfer is the from air into the snowpack when

where RH_nuet = the neutral relative humidity at which no latent heat flux occurs. During the ablation period, the snow surface temperature is 0°C (32°F) and the saturated vapor pressure above the snowpack, e_sat(Tss) can be calculated directly. The neutral relative humidity under these conditions can be estimated as a function of the air temperature index (the degrees that the air temperature is above 32°F) and is shown in Figure below.

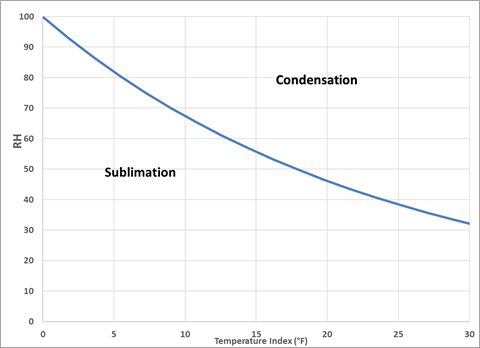
It can be seen in Figure that sublimation of the snowpack will not be an uncommon occurrence during the ablation period, even when the air temperature is 10°F above freezing or more. During the ablation period, the sensible and latent heat fluxes will often be in different directions: the sensible heat flux into the snowpack and the latent heat flux out of the snowpack. The latent heat flux will be into the snowpack generally only during periods of high relative humidity, for example rain on snow events, fog, and other periods when very moist air is present.

The rates of sensible and latent heat transfer are both determined by the degree of turbulence in the atmosphere above the snow and the stability of the atmosphere. The primary way by which turbulence is generated is by wind drag over the snow and ground surface. The rate of the turbulent energy generation is very sensitive to the velocity of the wind. The ability of wind to increase the heat transfer rate is called convection. However, wind is not the only creator of turbulence in the atmosphere – natural convection of sensible and latent heat from the snow and ground surface can also create turbulence. Natural convection occurs when the density of the air immediately at the snow surface is less than the density of the air above. This difference in density causes the air to rise vertically upwards though buoyancy. The atmosphere is said to unstable when natural convection occurs. Mixed convection occurs when wind convection is augmented by natural convection. A contrasting case occurs when the atmosphere is stable – that is the air near the ground is denser than the air above. Under stable conditions, natural convection does not occur and the wind convection is damped. Under very stable conditions convection may not occur at all if the wind velocity is low, and sensible and latent heat transfer can drop to very low levels.

The rates of sensible and latent heat transfer can be calculated using formulas such as

$\begin{array}{l}Q_{\text {Latent }}=\rho_{a} L_{v} C_{L} U_{Z}\left(e_{a}-e_{\operatorname{sat}\left(T_{\text {snow }}\right)}\right) \\ Q_{\text {sensible }}=\rho_{a} c_{p a} C_{s} U_{Z}\left(T_{a}-T_{\text {snow }}\right)\end{array}$

Where Q_Latent = the rate of latent heat transfer; Q_sensible = the rate of sensible heat transfer; ρ_a = the density of air; L_v = the latent heat of sublimation; C_pa = the heat capacity of air; U_Z = the wind speed measured at an elevation Z; e_a = the water vapor pressure in the atmosphere; e_sat(Tsnow)= the saturated vapor pressure immediately above the snow surface; T_a = the air temperature; and T_snow = the snow surface temperature. C_L and C_s are stability factors that account for the influence of the stability of the atmosphere on the rates of sensible and latent heat transfer. There are a variety of ways of estimating the stability factors, but often they are presented as functions of the dimensionless bulk Richardson Number (Ri). Ri is calculated as

$\begin{array}{l}\displaystyle R i=\frac{g Z\left(T_{a}-T_{\text {snow }}\right)}{0.5\left(T_{a}+T_{\text {snow }}\right) U_{Z}^{2}}\end{array}$

where g = the acceleration of gravity. When Ri >0, (that is, T_a > T_snow) the conditions are stable, and the stability factor tends to be small, indicating that sensible and latent heat transfer rates are small. If Ri >>0 then any convection is effectively damped and the transfer rates drop to near zero. When Ri = 0 (T_a = T_snow), the conditions are neutral, and the heat transfer is controlled by forced convection. When Ri < 0 (T_a < T_snow), the conditions are unstable, and the stability factor tends to be large, indicating that the sensible and latent heat transfer rates are greater due to augmentation of forced convection by natural convection. Representative values of the stability factors are shown in Figure below.

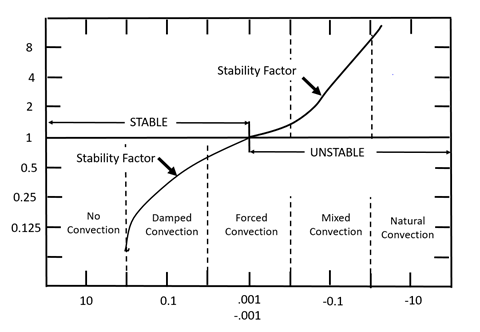
During the ablation period, the snow surface temperature is 0°C (32°F) and the air temperature is generally greater than 0°C (32°F) which means that T_a > T_snow and Ri > 0 and the atmosphere is stable. The atmosphere becomes more and more stable as the air temperature increases relative to the snow surface temperature. This means that the turbulent fluxes of latent and sensible heat are effectively suppressed by the increasing stability of the air during the ablation period unless there is a significant wind velocity.

Longwave Radiation Heat Transfer

All bodies possessing energy emit electromagnetic radiation (and this is always true if their temperature is above absolute zero). The amount of radiation emitted by a body at each wavelength of the electromagnetic spectrum is determined by the temperature of the surface of the body according to Planck’s Law. (Longwave radiation of bodies with surface temperatures in the range of temperatures found near the earth’s surface typically emit radiation at wavelengths between 4 and 50 μm.) The total longwave radiation emitted by a body per unit area can be calculated by integrating over all frequencies to arrive at the Stefan-Boltzmann Law

$\begin{array}{l}\displaystyle Q_{LW} = \varepsilon T^4_S\end{array}$

where Q_LW = the longwave radiation emitted per unit time per unit area; σ = the Stefan-Boltzmann constant (5.67 x 10^-8 W m^-2 °K^-1); T_s = the surface temperature in degrees Kelvin; and ε = the emissivity of the surface (emissivity is between 0 and 1. If a body is a “perfect” emitter of radiation, ε = 1. In fact, many bodies, such as snow and vegetation are close to being perfect emitters).

Longwave radiation is emitted by the snow surface according to the Stefan-Boltzmann Law. This is known as upwelling (or outgoing) radiation. The upwelling longwave radiation emitted by the snow surface is energy lost from the snow that cools the snow. The longwave radiation emitted by the snow surface is found as

$\begin{array}{l}\displaystyle Q_{LW}\uparrow = \varepsilon T^4_S\end{array}$

where ε_s = the emissivity of the snow surface (accepted values range from .97 to 1.0); and T_snow = the temperature of the snow surface (°K).

There is also downwelling (or incoming radiation) emitted from the atmosphere itself and by vegetation and structures in the vicinity. The downwelling radiation absorbed by the snow surface is energy gained by the snow that warms the snow. The overall impact of longwave radiation is found by summing the downwelling and upwelling longwave radiation at the surface:

$\begin{array}{l}\displaystyle Q_{LWnet} = Q_{LW\uparrow} + Q_{LW\downarrow}\end{array}$

where Q_LWnet = the net longwave at the snow surface; and Q_LW_â = the downwelling longwave radiation. The longwave radiation emitted by the atmosphere that reaches the snow surface is

$\begin{array}{l}\displaystyle Q_{LWa\downarrow} = \varepsilon_{a(e_a,T_a,clf)}\sigma T_a^4\end{array}$

where ε_a = the emissivity of the atmosphere. ε_a is affected by the vapor pressure (e_a), air temperature (T_a), and cloud cover (clf). The cloud cover is parameterized by the sky cloud fraction, with clf = 1 for a complete cloud cover, clf = 0 clear skies. ε_a can be estimated by a variety of formulas. A representative formula is

$\begin{array}{l}\displaystyle \varepsilon_a(clf+(1-clf)\varepsilon_{cl})\end{array}$

where ε_cl = the clear-sky emissivity. Note that as clf increases from 0 to 1, ε_a proportionally increases between the clear sky value, ε_cl and the limiting value of 1 for a completely cloud covered sky. The clear-sky emissivity is often estimated as

$\begin{array}{l}\displaystyle \varepsilon_{cl} = 0.68+0.036\sqrt{e_a}\end{array}$

The equation for the downwelling longwave radiation from the atmosphere can be found by combining the above equations as

$\begin{array}{l}\displaystyle Q_{L W a \downarrow}=\left(c l f+(1-c l f)\left(0.68+0.036 \sqrt{e_{a}}\right)\right) \sigma T_{a}^{4}\end{array}$

The downwelling longwave radiation from the atmosphere is relatively small during cold, clear periods with low humidity (clf = 0, e_a ~0, ε_cl ~0.68). It is relatively large during warm cloud covered periods (clf = 1, ε_cl =1).

Downwelling longwave radiation can also be emitted by the vegetative canopies above the snow surface. The total downwelling radiation can be described as the sum of the radiation from the sky and the vegetative canopies as

$\begin{array}{l}\displaystyle Q_{L W \downarrow}=S_{v f} Q_{L W a \downarrow}+\left(1-S_{v f}\right) Q_{L W \downarrow}\end{array}$

where Q_LWv_â = the longwave radiation emitted by the canopy. The vegetative canopy is parameterized by the sky view factor, S_vf, with S_vf, = 1 if there is no vegetative canopy above the snow, and S_vf = 0 if the view of the sky is completely blocked by the canopy. The longwave radiation emitted by the canopy is estimated as

$\begin{array}{l}\displaystyle Q_{LW\downarrow} = \sigma T_a^4\end{array}$

The branches, stems, leaves, and other components of the vegetative canopy are generally assumed to have an emissivity of 1 and their temperature assumed to be equal to the air temperature.

The net longwave radiation at the snow surface can now be written as

$\begin{array}{l}\displaystyle Q_{L W n e t}=S_{v f} Q_{L W a \downarrow}+\left(1-S_{v f}\right) Q_{L W \downarrow}-Q_{L W \uparrow}\end{array}$

Note the upwelling longwave radiation emitted by the snow surface has been given the opposite sign of the downwelling radiation. Expanding this equation

$\begin{array}{l}\displaystyle Q_{L W_{n e t}}=S_{v f} \varepsilon_{a} \sigma T_{a}^{4}+\left(1-S_{v f}\right) \sigma T_{a}^{4}-\varepsilon_{s} \sigma T_{s n o w}^{4}\end{array}$

Shortwave Radiation Heat Transfer

Shortwave radiation is radiation produced by the sun that reaches the surface of the earth. The sun, like all bodies, emits radiation determined by the temperature of the surface of the body according to Planck’s Law. The intense temperature of the sun (about 10,000°F or 5,500°C) produces the majority of its radiation in the wavelengths from 0.295 to 2.85 μm. The human eye is sensitive to wavelengths between about 0.390 to 0.700 μm. It is the shortwave radiation from the sun that the human eye uses to see.

In the context of snow hydrology, shortwave radiation is not approached wavelength by wavelength but rather in terms of the broadband value of downwelling shortwave radiation. The broadband value of shortwave radiation is found through a weighted integration of the downwelling shortwave radiation at each wavelength that comprises shortwave radiation. When shortwave radiation reaches the snow surface a portion is reflected and a portion absorbed. It is only the absorbed portion that can change the snowpack temperature and/or cause snowmelt. The ability of snow to reflect shortwave radiation is determined by the albedo of the snow, α. The energy absorbed by the snow is

$\begin{array}{l}\displaystyle Q_{SW} = (1-\alpha)Q_{SW\downarrow}\end{array}$

where Q_SW = the shortwave radiation absorbed at the snow surface; Q_SW_â = the downwelling shortwave radiation that reaches the snow surface; and α = the albedo of the snow (0< α <1)

Albedo.

Albedo is the ratio of the reflected shortwave radiation to the downwelling shortwave radiation reaching the surface. It is well known that the albedo of snow varies wavelength by wavelength. However, in snow hydrology, it is generally the broadband albedo that is of interest. The broadband albedo is found through a weighted integration of the albedo at each wavelength that comprises shortwave radiation. The albedo is determined by the crystalline structure of the snowpack surface. Shortwave radiation tends to be reflected by the surface of ice crystals and absorbed in the interior of crystals. As mentioned above, newly fallen snow typically has large surface areas to volume ratios. As a result, the albedo of newly fallen snow is large, generally in the range of 0.85-0.95. Snow metamorphism is the modification of the snow crystals and grains to less angular, more rounded forms with time. Metamorphism increases the size of the crystals which decreases the surface area and increases their volume. This causes the albedo to decline as the metamorphism progresses. As long as the air temperature is less than 0°C (32°F), metamorphism proceeds slowly and the rate of decline of the albedo is relatively slow. Each new snowfall ‘resets’ the albedo back to the newly fallen value and the metamorphism and albedo decline start over again. However, when the air temperature is greater than 0°C (32°F) and active snowmelt is occurring, metamorphism occurs quickly and the rate of decline of the albedo is relatively rapid. The albedo can decline to values of about 0.40 for well-aged snow. The albedo may drop to even lower values when the snowpack is shallow (snow depths of 0.5 m or less) allowing the ground surface beneath the snow to have an influence. Dust, soot, forest debris such as bark and twigs, and other deposited matter can also influence the snow surface albedo, and generally cause it to decline.

Three winters of albedo measurements and snow depth observations in the Senator Beck basin in Colorado. The sold blue circles are the daily average snow albedo, the open blue circles are the daily average albedo when the snow depth was reported as zero, and the orange line is the daily average snow depth.

Modeling Downwelling shortwave radiation.

Many factors can influence the amount of shortwave radiation reaching the ground at any location. The journey of shortwave radiation begins at the surface of the sun where it is emitted. It then travels through space for a short span of 8 minutes and 20 seconds to reach the top of the atmosphere of the earth. This top-of-the-atmosphere value can be directly calculated as

$\begin{array}{l}\displaystyle I_{o \downarrow}=S_{0}\left(\frac{r_{0}}{r}\right)^{2} \cos \theta_{0}\end{array}$

where I₀_â = the top of the atmosphere shortwave radiation (Wm^-2); r₀ = the mean distance between the earth and sun; r = the actual Earth-Sun distance; S₀ = the solar constant at the mean Earth-Sun distance r₀(1369.3 w/m²); and q₀ = the solar zenith angle, the angle measured at the earth's surface between the location of the sun in the sky and the local zenith (The local zenith is the point in the sky directly above a particular location.) The Earth-Sun distance r varies throughout the year because the earth follows a slightly elliptical orbit around the sun. Each of these geometrical parameters in this equation, r₀, r, and q₀, can be calculated with precision because the clockwork nature of the earth’s orbit around sun and the obliquity (tilt) of the earth itself are both well understood. (Whether or not the solar constant, S₀, is, in fact, a constant is a question beyond the scope of this write up. Certainly, ongoing observations suggest that any variations are relatively small.) The formulas for the geometrical parameters are straightforward but computationally intensive if done by hand. In short, the top of the atmosphere shortwave

radiation can be calculated precisely for any location on earth for any time if the following are known: day of year, latitude, longitude, time of day, and offset from Greenwich Mean Time. The portion of the top of the atmosphere shortwave radiation that actually reaches the surface of the earth depends on the conditions of the atmosphere, - primarily the presence of clouds. The earth’s atmosphere is not perfectly transparent to all the shortwave radiation even on a cloud free day when some radiation will be scattered, absorbed by gases and water vapor, and scattered by aerosol particles. These reductions in solar radiation on cloud-free days will tend to be relatively small unless the atmosphere is particularly turbid.

Clouds have a major impact on the sunlight reaching the earth. The impact will vary depending on the location of clouds relative to the position of the sun, the type of clouds, and the percentage of the sky covered by clouds. An example relationship describing the shortwave radiation absorbed by a horizontal snow surface given the top of atmosphere value can be written

$\begin{array}{l}\displaystyle Q_{s w}=(1-\alpha) a_{t}\left(1-0.65 c l f^{2}\right) I_{0 \downarrow}=(1-\alpha) Q_{s w \downarrow}\end{array}$

where a_t = an attenuation factor due to dust, scattering and absorption by the atmosphere (a_t < 1); clf = the sky cloud factor (0 < clf < 1); α = the snow albedo; I_o_â = the top of the atmosphere shortwave radiation; and Q_SW_â = the shortwave radiation reaching the snow surface. If the snow surface is not horizontal corrections can be made based on the slope and aspect of the immediate topography. Shadows from surrounding terrain can also impact the downwelling shortwave radiation.

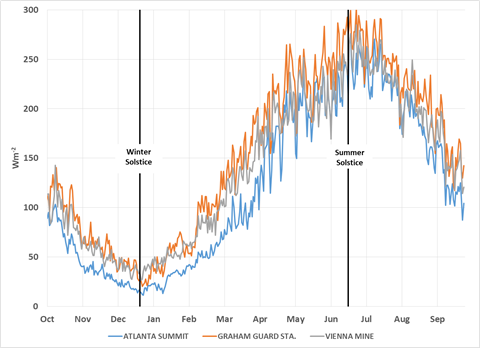
The top of the atmosphere shortwave radiation arriving at any location follows a seasonal cycle. In the Northern Hemisphere, the minimum top of the atmosphere radiation occurs at the winter solstice (December 21^st). The value of the daily average shortwave radiation at the winter solstice decreases from south to north. North of the Arctic Circle (66° 33′ 47.3”), the daily average shortwave radiation is zero at the winter solstice because north of the Arctic Circle is continually dark at that time of year. As the season progresses in time the solar radiation increases at every latitude in the northern hemisphere reaching a maximum on the summer solstice (June 21^st). The relative change from winter minimum to summer maximum is greatest in the northern latitudes and less in the southern. The further south a position is located the earlier in the year it will reach a given level of solar radiation above its minimum. At the summer solstice the daily average shortwave radiation is remarkably uniform from the North Pole to the equator. However, the length of the sunlit portion of the day also varies from the North where there are 24 hours of continuous daylight to a minimum at the equator where there are 12 daylight hours. This means that the instantaneous or hourly radiation is less in the north because the daily average is applied over more hours of daylight.

Daily average broadband downwelling shortwave radiation measured at three SNOTEL sites located in the same region of Idaho. Each day has been averaged all years in the POR.

Precipitation heat transfer

Heat can be transferred into the snowpack by precipitation. The heat transfer process is very different depending on the form of the precipitation, rain or snow. In the HEC-HMS Temperature Index Snow Model, the form of the precipitation is determined by comparing the air temperature, T_a, to the rain/snow determinate temperature, also known as the PX temperature, or T_PX. If the air temperature is warmer than the PX temperature, T_a > T_PX, than the precipitation is falling as rain. If the air temperature is less than or equal to the PX temperature, T_a £ T_PX, than the precipitation is falling as snow. T_PX.is considered a constant, and is set by the model user. In general, T_PX is usually set warmer than the ice/water equilibrium temperature (32°F (0°C)), by a small margin.

Snowfall.

The precipitation is falling as snow when T_a £ T_PX. The sensible heat that arrives at the surface of the snowpack due to snowfall is

$\begin{array}{l}\displaystyle Q_{snow}=\rho_wC_{p\_ ice}S_tT_a\end{array}$

where S_t = the snowfall rate in terms of the snow water equivalent (depth/time); and T_a = the air temperature. Note that it is assumed that the temperature of the snowfall is the same as the air temperature, T_a. The snowfall sensible heat may or may not have an impact on the average snowpack temperature. This can be determined by restating equation as

$\begin{array}{l}\displaystyle \rho_{w} C_{p_{-} i c e} \frac{d S W E_{t} \bar{T}_{t}}{d t}=Q_{\text {snow }}=\rho_{w} C_{p_{-} i c e} S_{t} T_{a}\end{array}$

Which can be expanded into

$\begin{array}{l}\displaystyle \rho_{w} C_{p_{-} i c e}\left(\bar{T}_{t} \frac{d S W E_{t}}{d t}+S W E \frac{d \bar{T}_{t}}{d t}\right)=\rho_{w} C_{p_{-} i c e} S_{t} T_{a}\end{array}$

Note that the rate of change in SWE is equal to the snowfall rate, which is stated as

$\begin{array}{l}\displaystyle \frac{dSWE}{dt}=S_t\end{array}$

Substituting equation into equation , the change in the average snowpack temperature, , due to snowfall is

$\begin{array}{l}\displaystyle \frac{d \bar{T}_{t}}{d t}=\frac{S_{t}\left(T_{a}-\bar{T}_{t}\right)}{S W E_t}\end{array}$

The average snowpack temperature, , will be changed by snowfall only if the air temperature and are different.

The above equation can also be stated in terms of the Cold Content, Cc. First, the definition of Cold Content, as written in equation , is restated in terms of SWE

$\begin{array}{l}\displaystyle C_{c}=-\frac{\bar{\rho}_{s}}{\rho_{w}} D \frac{C_{p i c} \Delta T}{\lambda}=-S W E \frac{C_{p i c e}\left(T_{M}-\bar{T}\right)}{\lambda}\end{array}$

The change of cold content with time can be found by taking the derivative of equation with respect to time and substituting in the expression for the rate of change of the average snowpack temperature, , from equation

$\begin{array}{l}\displaystyle \frac{d C_{c}}{d t}=-S_{t} \frac{C_{p i c e}\left(T_{M}-T_{a}\right)}{\lambda}\end{array}$

The rate of change of the Cold Content is described by , however, this can be stated in a more compact form if the rate that Cold Content arrives as snowfall, is defined as

$\begin{array}{l}\displaystyle C_{c_{-} p r e c i p}=-S_{t} \frac{C_{p i c e}\left(T_{M}-T_{a}\right)}{\lambda}\end{array}$

Then

$\begin{array}{l}\displaystyle \frac{dC_C}{dt}=C_{c\_ precip}\end{array}$

Rainfall.

The precipitation is falling as rain when T_a > T_PX. Rainfall impacts the energy balance of the snowpack through the sensible heat that it brings to the snowpack and the through the possibility of phase change of the liquid water. The sensible heat is a determined by the temperature of the rain when it reaches the snow surface. Once the liquid water has cooled to the ice/water equilibrium temperature further heat extraction must result in phase change of the liquid water to ice. Generally, freezing of rainfall in the snowpack can only happen if the snowpack temperature is less than the ice/water equilibrium temperature.

The sensible heat that arrives at the surface of the snowpack due to rainfall is

$\begin{array}{l}\displaystyle Q_{\text {rain_sensible }}=\rho_{w} C_{p_{-} \text {water }} P_{t}\left(T_{a}-T_{m}\right)\end{array}$

where P_t = the rainfall rate (depth/time); and T_a = the air temperature. Note that it is assumed that the temperature of the rainfall is the same as the air temperature, T_a. Also note that the water can only be cooled to T_m,the ice/water equilibrium temperature (32°F (0°C)).

Once the liquid water has reached the ice/water equilibrium temperature further cooling must result in phase change of the liquid water to ice. Generally, freezing of rainfall in the snowpack can only happen if the snowpack temperature is less than the ice/water equilibrium temperature. Freezing of rainfall in the snowpack is a very effective means of raising the snowpack temperature due to the latent heat released by the liquid water when it freezes.

The potential latent heat that arrives at the surface of the snowpack due to rainfall is

$\begin{array}{l}\displaystyle Q_{rain\_latent}=\rho_w \lambda P_t\end{array}$

Note that latent heat will be extracted from the liquid rainfall only as long as the snowpack temperature, , is less than the ice/water equilibrium temperature (32°F (0°C)), T_m.

$\begin{array}{l}\displaystyle Q_{\text {total }}=Q_{\text {latent }}+Q_{\text {sensible }}+(1-\alpha) Q_{S W \downarrow}+Q_{L W \downarrow}+Q_{L W \uparrow}+Q_{\text {Precipitation }}+Q_{\text {Ground }}\end{array}$