Download PDF
Download page Selecting a Transform Method.
Selecting a Transform Method
While a subbasin element conceptually represents infiltration, surface runoff, and subsurface processes interacting together, the actual surface runoff calculations are performed by a transform method contained within the subbasin. A total of nine different transform methods are provided. The choices include various unit hydrograph methods, a kinematic wave implementation, a linear quasi-distributed method, and a two-dimensional (2D) diffusion wave method.
The transform method for a subbasin is selected on the Component Editor for the subbasin element as shown in Figure 1. Access the Component Editor by clicking the subbasin element icon on the "Components" tab of the Watershed Explorer. You can also access the Component Editor by clicking on the element icon in the basin map, if the map is currently open. You can select a transform method from the list of seven available choices. If you choose the None method, the subbasin will transform all excess precipitation as runoff at the end of each time step. Use the selection list to choose the method you wish to use. Each subbasin may use a different method or several subbasins may use the same method.
When a new subbasin is created, it is automatically set to use the default transform method specified in the program settings. You may change the transform method for a subbasin at any time using the Component Editor for the subbasin element. Since a subbasin can only use one transform method at a time, you will be warned when changing methods that the old parameter data will be lost. You can turn off this warning in the program settings. You can change the transform method for several subbasins simultaneously. Click on the Parameters menu and select the Transform | Change Method command. The transform method you choose will be applied to the selected subbasins in the basin model, or to all subbasins if none are currently selected.
The parameters for each transform method are presented on a separate Component Editor from the subbasin element editor. The "Transform" editor is always shown near to the "Loss" editor. The kinematic wave method uses multiple tabs in the Component Editor. The information shown on the transform editor will depend on which method is currently selected.
Clark Unit Hydrograph Transform
The Clark unit hydrograph is a synthetic unit hydrograph method. This means that the user is not required to develop a unit hydrograph through the analysis of past observed hydrographs. Instead, a time versus area curve (time-area curve) is used to develop the translation hydrograph resulting from a burst of precipitation. The resulting translation hydrograph is routed through a linear reservoir to account for storage attenuation effects across the subbasin. There are three methods available for the Clark unit hydrograph: Standard, Variable Parameter, and Maricopa County AZ USA. The Component Editor will automatically update based on the selected method.
Standard
The Component Editor, when using the Standard method, is shown in Figure 2.
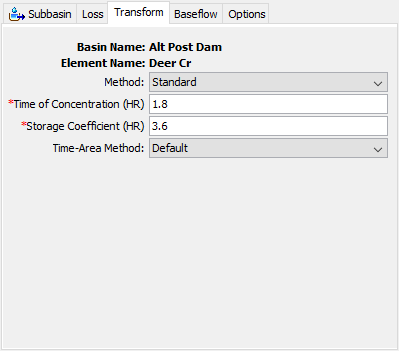
The time of concentration defines the maximum travel time in the subbasin. It is used in the development of the translation hydrograph.
The storage coefficient is used in the linear reservoir that accounts for storage effects. A dimensionless ratio can be defined as the storage coefficient divided by the sum of the time of concentration and storage coefficient. Many studies have found that the dimensionless ratio is relatively constant over a region.
Variable Parameter
Unit hydrograph theory assumes a linear relationship between precipitation and the runoff response. This assumption can lead to errors in timing and peak magnitude when simulating events that result from extremely large excess precipitation rates, such as the Probable Maximum Precipitation. When using the Clark unit hydrograph, tables relating time of concentration and storage coefficient to the excess precipitation can be used to vary the runoff response throughout the simulation. The Component Editor, when using the Variable Parameter method, is shown in Figure 3.
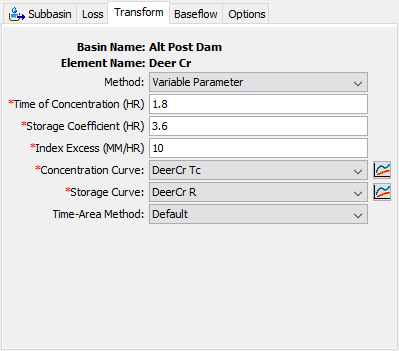
The "Index Excess" is an excess precipitation rate that is used to relate the time of concentration and storage coefficient defined in the editor against the variable parameter relationships. Typically, this rate is 1 inch/hour (or 1 mm/hour).
The variable parameter relationships must be defined as percentage curves in the paired data manager before they can be used in the subbasin element. These curves must be monotonically increasing. The x-axis of the percentage curves defines the excess precipitation rate relative to the index excess. The y-axis of the percentage curves defines either the time of concentration or storage coefficient for each percent excess precipitation rate (again, relative to the index excess).
The default time-area curve represents the subbasin using an elliptical shape. This shape has been shown to approximate the timing of surface runoff very well for typical subbasins. However, there is also an option to provide a user-specified time-area curve. The relationship must be defined as a percentage curve in the paired data manager before it can be used in the subbasin element. The independent axis of the percentage curve defines the percentage of the time of concentration, while the dependent axis of the curve defines the cumulative percentage of subbasin area contributing runoff. The curve must be monotonically increasing.
Maricopa County AZ USA
The Component Editor, when using the Maricopa County AZ USA method, is shown in Figure 4.
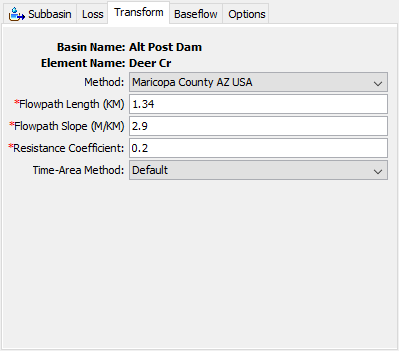
The Clark time of concentration and storage coefficient parameters are automatically computed using physical characteristics of the watershed and the following two equations.
| T_{c}=11.4 L^{0.5} K_{b}^{0.52} S^{-0.31} i^{-0.38} |
| R=0.37 T_{c}^{1.11} A^{-0.57} L^{0.80} |
L is the length of the hydraulically longest flow path, S is the watercourse slope of the longest flow path, Kb is the resistance coefficient, and i is the average excess precipitation intensity. L, Kb, and S are estimated and specified by the user into the Component Editor. Refer to the Maricopa County Drainage Design Manual for information about estimating L, Kb, and S (Maricopa County, 2011). The average excess precipitation intensity must be computed from the top ten highest five-minute time interval values. The HEC-HMS compute process will perform a preliminary simulation to compute precipitation loss/excess at a five-minute time interval (only when the Maricopa County AZ USA method is selected), regardless of the user defined simulation time-step. After running a preliminary simulation at a five-minute time-step, the program will extract the top ten highest five-minute time interval excess precipitation values, compute an average excess precipitation rate, and then compute the time of concentration and storage coefficient.
HEC-HMS issues a couple of notes in the Message Window indicating the computed average excess precipitation intensity, time of concentration, and storage coefficient. Note 45820 contains information about the computed average excess precipitation intensity. Note 45917 displays the computed time of concentration and storage coefficient.
Kinematic Wave Transform
The kinematic wave method is designed principally for representing urban areas, although it can be used for undeveloped regions as well. It is a conceptual model that includes one or two representative planes. Typically, one plane is used for impervious surfaces and one for pervious surfaces. Examples of impervious surfaces include building roofs, parking lots, and streets. Examples of pervious surfaces include lawn, parks, and undeveloped open space. The key difference in impervious and pervious surfaces is whether the surface allows infiltration. The same meteorologic boundary conditions are applied to each plane. However, separate canopy, surface, and loss rate information is required for each plane and is entered separately. The kinematic wave equations are used to calculate runoff for each plane and then a weighted composite runoff is calculated using the representative percentage for each plane.
The composite runoff is directed to a subcollector. The subcollector is used to represent primary collection in the stormwater management system. The most common collection system is gutters along streets. In areas without gutters, unlined ditches next to the street may perform a similar stormwater collection function. The composite runoff is applied to the subcollector as a uniform lateral boundary condition, scaling based on the representative area of a typical subcollector. Water is routed through a representative subcollector using the kinematic wave equations. There is no seepage from the subcollector so it may be difficult to use it for representing vegetated swales and other types of best management practices.
The outflow from the representative subcollector is directed to a collector. The collector is used to represent the next step up in the stormwater management system. Conceptually, the collector receives inflow from multiple gutters or ditches. A common collector is a concrete channel about two or three meters wide. The outflow from the subcollector is scaled up using the representative area of a typical collector and applied to the collector as a uniform lateral boundary condition. Water is routed through a representative collector using the kinematic wave equations. Again, there is no seepage from the collector.
The outflow from the representative collector is directed to a channel. The channel may be used to represent the final step in the stormwater management system, or optionally may be used to represent the river passing through the subbasin. Conceptually, the channel receives inflow from multiple collectors. The outflow from the representative collector is scaled up using the area of a typical collector and the area of the subbasin. The scaled flow is applied to the channel as a uniform lateral boundary condition. Water is routed through the channel to become the outflow from the subbasin. The routing may be performed using either the kinematic wave equations or the Muskingum Cunge equations.
Planes
A separate tab is provided for each plane; they are displayed whenever the Component Editor is shown for the subbasin as seen in Figure 5.
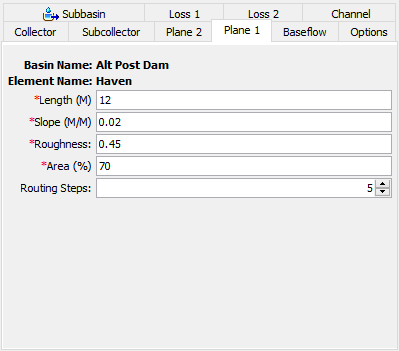
The first parameter is the length. The typical length of the conceptual plane should be entered. For impervious areas, this should be the average flow length from the point where precipitation falls, to where the runoff first enters a collection gutter or channel. For pervious areas, this should likewise be the average flow length. When using the two planes to represent pervious and impervious areas, it is helpful to adopt a convention for which plane number (one or two) represents the pervious area.
The slope is also required for each plane that will be used. The slope should represent the average slope along the flow line from the point where precipitation falls to where the runoff first enters a gutter or channel.
Roughness is the principal difference between a plane meant to represent impervious or pervious area. Roughness coefficients for natural areas are much higher than for developed areas. However, in both cases the surface roughness coefficients are higher than typical Manning's roughness coefficients used for open channel flow.
The percentage of the subbasin area occupied by each plane must be entered. If you only want to use one plane, then enter 100 for the first plane and 0 for the second. You do not need to enter length, slope, or roughness if the area will be set to zero.
The number of routing steps is used as a hint to the program when it determines the correct distance step to use during runoff calculations. Criteria based on rate of precipitation and other factors are used to automatically determine the correct distance and time steps for solving the kinematic wave equation. The default value is five.
Subcollector and Collector
A separate tab is provided for the subcollector and collector as shown in Figure 6.
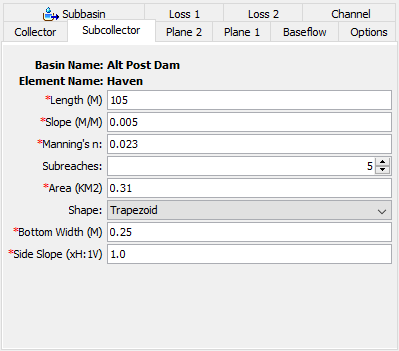
The length should be the average distance from the beginning of the subcollector to where it will enter a collector. Usually this value will be measured from maps of the stormwater collection system.
The slope should be the average slope along the average flow length. This value may be estimated from maps if they provide sufficient vertical resolution. Field survey data may be necessary to actually determine elevations of the gutter or channel. If the slope varies significantly throughout the system, this may become a determining factor in how the system is broken into subcollectors, collectors, and main channel.
The Manning's n roughness coefficient should be the average value for the whole subcollector. It is important to remember that the parameter data entered for the subcollector should be typical of all similar subcollectors in the subbasin.
The number of subreaches is used as a hint to the program when it determines the correct distance step to use during routing calculations. The default value is five.
The typical area of each subcollector must be entered. This is used to determine how to apply the composite outflow from the subcollector to the collector channel. It essentially determines the number of subcollector channels in the subbasin.
Five options are provided for specifying the cross section shape: circle, deep, rectangle, trapezoid, and triangle. The circle shape cannot be used for pressure flow or pipe networks, but is suitable for representing a free water surface inside a pipe. The deep shape should only be used for flow conditions where the flow depth is approximately equal to the flow width. Depending on the shape you choose, additional information will have to be entered to describe the size of the cross section shape. This information may include a diameter (circle) bottom width (deep, rectangle, trapezoid) or side slope (trapezoid, triangle). The side slope is dimensionless and entered as the units of horizontal distance per one unit of vertical distance.
The outflow from the subcollector enters a collector as lateral inflow. The collector channel is intended to represent small ditches or open channels that are part of an engineered stormwater management system. The parameters for the collector are exactly the same as for the subcollector.
Length, slope, Manning's n, and the number of subreaches all have the same definitions. The area served by a typical collector must be entered; this is used to apply lateral inflow from the collector to the main channel. Options for the cross section shape are exactly the same as for the subcollector.
Channel
A separate tab is provided for the channel as shown in Figure 7.
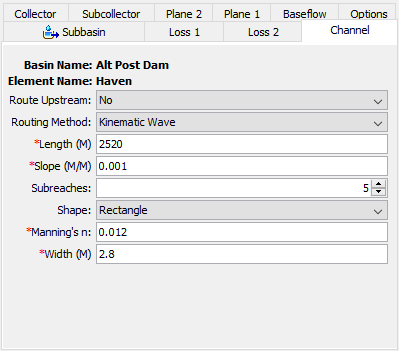
Normally it is not possible to connect upstream inflow to a subbasin element. However, because of the conceptual representation of the channel, it is possible to have an upstream inflow on the main channel. In order to connect upstream elements to the subbasin, you must select the "Route Upstream" option.
The surface runoff on the two planes is always routed using the kinematic wave method. However, you have the choice of using Muskingum-Cunge routing in the subcollector, collector, and main channel. All three channels use the same method. Select the method you wish to use.
If the route upstream option is turned on, the length should be the distance from the upstream boundary of the subbasin to the outlet. If the route upstream option is turned off, the length should be from the identifiable concentration point of the channel to the subbasin outlet. There is only one channel is each subbasin.
The slope should be the average slope for the whole channel. This value may be estimated from maps if they provide sufficient vertical resolution. Field survey data may be necessary to actually determine elevations of the channel bed for calculating the slope.
The number of subreaches is used to determine the distance step to use during routing calculations. The default value is five. This parameter is only entered when the kinematic wave routing method is selected. For natural channels that vary in cross section dimension, slope, and storage, the number of subreaches can be treated as a calibration parameter. The number of subreaches may be used to introduce numerical attenuation which can be used to better represent the movement of floodwaves through the natural system.
A cross section shape must be selected. If the kinematic wave routing method is selected, the options will include circle, deep, rectangle, trapezoid, and triangle. When the Muskingum-Cunge routing method is selected, the options will include circular, rectangle, tabular, trapezoid, triangle, and eight point. You will have to enter a Manning's n roughness value for the channel. If the tabular shape is used, you will also have to select multiple curves that describe the way in which discharge, area, and top width changes with elevation. These curves must be defined as elevation-discharge, elevation-area, and elevation-width functions, respectively, in the paired data manager before they can be used in the reach element. These curves must be monotonically increasing. Within each of the aforementioned curves, the x-axis defines the elevation while the y-axis defines the variable of interest. Elevations must be monotonically increasing. If the eight point cross section shape is used, you will also have to enter a roughness value for the left and right overbank areas. You will have to enter other appropriate parameters data based on the cross section choice.
ModClark Transform
The ModClark method is a linear, quasi-distributed transform method that is based on the Clark conceptual unit hydrograph. It fundamentally represents the subbasin as a collection of grid cells. The Clark method uses a time-area curve and the time of concentration to develop a translation hydrograph. By contrast, the ModClark method eliminates the time-area curve and instead uses a separate travel time index for each grid cell. The travel time index for each cell is scaled by the overall time of concentration. Excess precipitation falling on each grid cell is lagged by the scaled time index and then routed through a linear reservoir. The outputs from the linear reservoirs of the cells are combined to produce the final hydrograph.
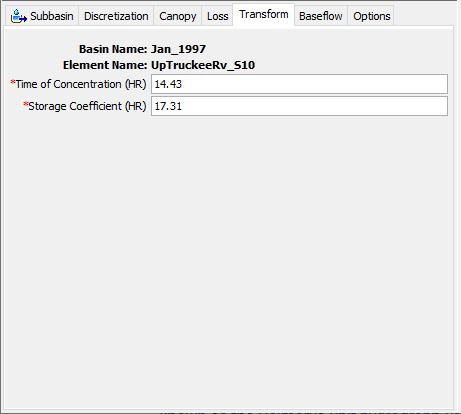
The time of concentration defines the maximum travel time in the subbasin. The grid cell in the subbasin with the largest travel time index will have exactly this specified time of concentration. All other grid cells will have a scaled time of concentration based on the ratio of the cell's travel time index to the maximum travel time index.
The storage coefficient is used in the linear reservoir for each grid cell. The same coefficient is used for all cells in the subbasin.
Gridded information (e.g. cell size and travel length) must be supplied using either a File-Specified Discretization or a Structured Discretization. The Selecting a Discretization Method v4.7 section describes these options in more detail.
The Component Editor is shown in Figure 8.
SCS Unit Hydrograph Transform
The Soil Conservation Service (SCS) unit hydrograph method defines a curvilinear unit hydrograph by first setting the percentage of the unit runoff that occurs before the peak flow (NRCS, 2007). A triangular unit hydrograph can then be fit to the curvilinear unit hydrograph so that the total time base of the unit hydrograph can be calculated. The standard unit hydrograph is defined with 37.5% of unit runoff occurring before the peak flow. This definition corresponds to a peak rate factor of 484 which incorporates the percentage of unit runoff before the peak, calculated total time base, and unit conversions when applying the equations within the US Customary unit system. An example of the Component Editor is shown in Figure 9.
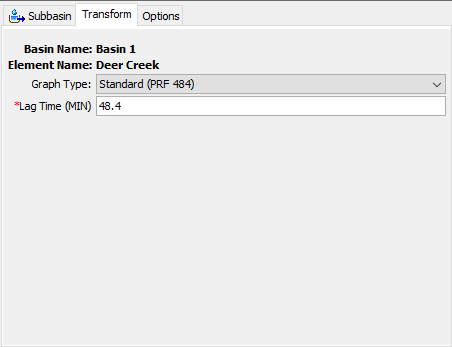
The percentage of unit runoff occurring before the peak flow is not uniform across all watersheds because it depends on flow length, ground slope, and other properties of the watershed. By changing the percentage of unit runoff before the peak, alternate unit hydrographs can be computed for watersheds with varying topography and other conditions that effect runoff. The percentage of runoff occurring before the peak is reflected in the peak rate factor (PRF). It has been found that flat watersheds typically have a lower PRF that may be as small as 100. Steeper watersheds have a larger PRF thay may range up to 600. The default unit hydrograph has a PRF of 484. Unit hydrographs with specific peak rate factors are defined in the National Engineering Handbook (NRCS, 2007). A very specific case of the unit hydrograph for flat coastal watersheds is known as the Delmarva unit hydrograph (Welle, Woodward, and Moody, 1980).
The standard lag is defined as the length of time between the centroid of precipitation mass and the peak flow of the resulting hydrograph. Examination of the equations used in deriving the curvilinear unit hydrograph show that the lag time can be computed as the duration of unit precipitation divided by two, plus 60% of the time of concentration.
Snyder Unit Hydrograph Transform
The Snyder unit hydrograph is a synthetic unit hydrograph method. The original data only supported computing the peak flow as the result of a unit of precipitation. Later, equations were developed to estimate the time base of the hydrograph and the width at 50% of the peak flow. Since it does not compute all ordinates of the hydrograph, a Clark hydrograph is created in such a way that the Snyder properties are maintained.
Standard
The standard method requires the user to estimate parameters using appropriate techniques. Many approaches have been proposed for estimating the parameters, relying on different physical properties of the watershed under consideration. The approaches are typically developed by fitting the unit hydrograph parameters for a watershed with observed precipitation and discharge data. These approaches may be effective at estimating parameters in ungaged watersheds if they are similar to the watersheds used to develop the approach. The Component Editor is shown in Figure 10.
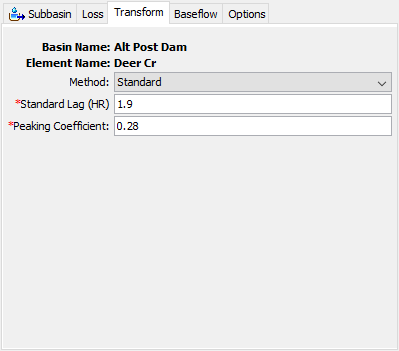
The standard lag is defined as the length of time between the centroid of precipitation mass and the peak flow of the resulting hydrograph. Many relationships for estimating lag from subbasin characteristics have been developed for different regions.
The peaking coefficient measures the steepness of the hydrograph that results from a unit of precipitation. It ranges typically from 0.4 to 0.8 with lower values associated with steep-rising hydrographs. It is estimated using the best judgement of the user, or possibly from locally-developed relationships to watershed physical features.
Ft Worth District
The Ft Worth method is the result of regional urban studies conducted by the U.S. Army Corps of Engineers, Ft. Worth District in the Dallas-Ft Worth, Austin, and San Antonio areas. The method is applicable for watersheds substantially similar to the watersheds included in the regional study. The user enters values for five physical characteristics of a subbasin. Equations from the regional study use the parameter values to calculate the Snyder standard lag. The Component Editor is shown in Figure 11.
The total length is measured from the outlet of the subbasin, along the main watercourse to the most hydraulically remote point on the subbasin boundary.
The centroid length is measured from the outlet of the subbasin, along the main watercourse, to a point opposite the subbasin centroid.
The weighted slope is the slope of the main watercourse between points located at 10 percent and 85 percent of the length of the main watercourse, measured from the subbasin outlet.
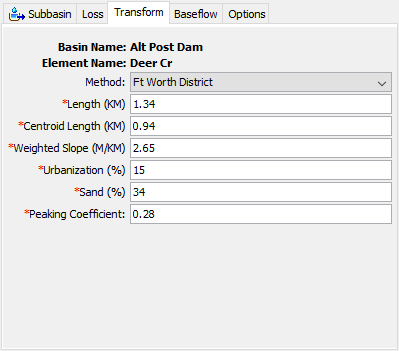
Urbanization percentage is estimated as the percentage of the subbasin where the drainage system has been improved to more efficiently carry runoff to the outlet. Such improvements may include street gutters, straightened channels, concrete lined channels, or other effeciencies. This parameter provides a way to account for the effects of urbanization on the hydrologic response of the subbasin.
The sand percentage accounts for the effect of infiltration and surface runoff properties on hydrograph generation. Zero percent indicates essentially all-clay soils with characteristically low infiltration rates. Conversely, 100 percent indicates essentially all-sandy soils with characteristically high infiltration rates.
The Fort Worth method does not include estimation of the peaking coefficient. This parameter must be estimated by another method and entered directly.
Tulsa District
The Tulsa method is the result of regional urban studies conducted by the U.S. Army Corps of Engineers, Tulsa District using watersheds across Oklahoma. The method is applicable for watersheds substantially similar to the watersheds included in the regional study. The user enters values for four physical characteristics of a subbasin. The values are used with equations developed in the regional study for estimating the standard lag and peaking coefficient. The Component Editor is shown in Figure 12.
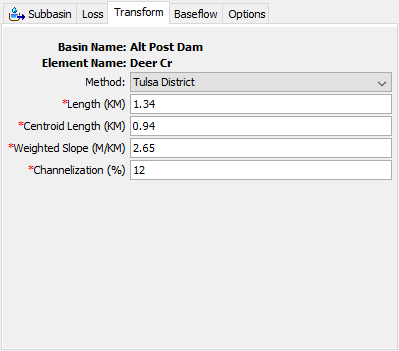
The total length is measured from the outlet of the subbasin, along the main watercourse to the most hydraulically remote point on the subbasin boundary.
The centroid length is measured from the outlet of the subbasin, along the main watercourse, to a point opposite the subbasin centroid.
The weighted slope is the slope of the main watercourse between points located at 10 percent and 85 percent of the length of the main watercourse, measured from the subbasin outlet.
Channelization percentage is estimated as the percentage of the subbasin where the drainage system has been improved to more efficiently carry runoff to the outlet. Such improvements may include street gutters, straightened channels, concrete lined channels, or other effeciencies. This parameter provides a way to account for the effects of urbanization on the hydrologic response of the subbasin.
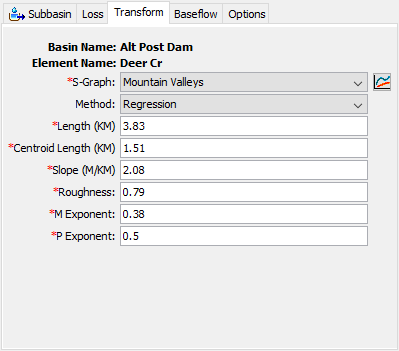
User-Specified S-Graph Transform
The user-specified s-graph method is not synthetic. It uses a special summation unit hydrograph (abbreviated as s-graph) to represent the response of a subbasin to a unit of precipitation. The s-graph is defined with percentage of the time lag as the independent variable (x axis), and percentage of the cummulative runoff volume as the dependent variable (y axis). Computationally, the s-graph is scaled by a specified time lag and then successive differences are taken along the curve to compute a unit hydrograph directly from the scaled s-graph. A given s-graph is generally only applicable in a particular region with subbasins that share certain characteristics.
The s-graph must be chosen from a selection list of percentage curves defined previously in the paired data manager. While percentage curves are used for other applications in the program, in this case they represent percentage of unit discharge versus percentage of time lag. You will not be able to use the selection list until you create at least one s-graph. If you wish, you can use the paired data button next to the selection list to open a chooser that will assist in selecting the correct s-graph. Click on a percentage curve to view its description. Descriptions are particularly important for percentage curves because of the different applications in the program.
Standard
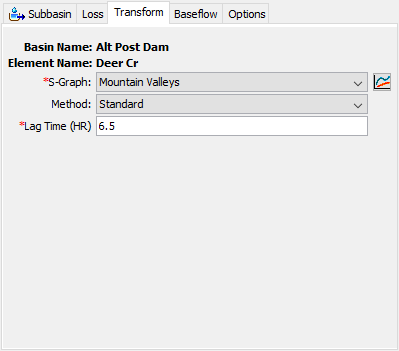
There are two different methods for specifying the lag time to be applied to the s-graph. The Standard method allows the simple specification of the lag time in hours. The lag time is defined as the length of time between the centroid of precipitation mass and the peak flow of the resulting hydrograph. An example of this method is shown in Figure 13.
Regression
The Regression method provides for the automatic calculation of the lag time using an equation commonly applied in regional regression studies. The equation is applied to the parameters within the context of the U.S. Customary unit system. If parameters are entered in System International units, then the equation is evaluated after converting the parameters to U.S. Customary equivalents. The equation takes the following form for computing the lag time in hours:
| t_{\text {lag}}=c\left(\frac{L * L_{c a}}{S^{p}}\right)^{m} |
The length of the longest flowpath in the subbasin is specified using the L parameter. The length along the stream from the outlet to a point opposite the centroid is specified by the Lca parameter. A typical stream slope must be specified as the s parameter. The C coefficient describes hydraulic efficiency of the stream channel. The m and p parameters should be found through a regional regression study of watershed properties and observed lag time. An example of this method is shown in Figure 14.
User-Specified Unit Hydrograph Transform
The user-specified unit hydrograph method is not a synthetic technique. Consequently, a separate unit hydrograph must be developed for each subbasin. Ideally these unit hydrographs are developed from multiple storm observations when precipitation and flow have been measured at similar time intervals. The unit hydrograph developed in this manner has a so-called duration that is equal to the duration of excess precipitation. For example, a 3-hour duration unit hydrograph is generated by a precipitation event with 3 hours of excess precipitation.
A unit hydrograph must be defined in the paired data manager before it can be used for a subbasin. An example of a unit hydrograph in the paired data manager is shown in Figure 15. Notice the duration and interval of the unit hydrograph are required. The duration must be set equal to the duration of excess precipitation used to develop the unit hydrograph. The interval is the time interval of the ordinates of the unit hydrograph. For example, a unit hydrograph developed from excess precipitation (which was uniformly distributed in space and time) over a duration of 3 hours can have a time interval of 15 minutes.
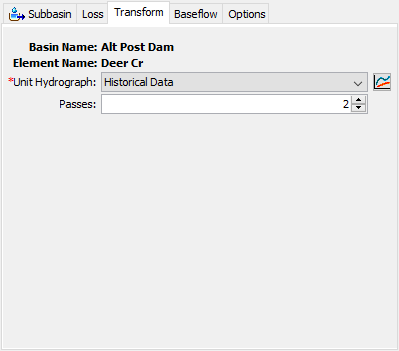
Information required for the user-specified unit hydrograph method is the selection of a unit hydrograph from the paired data manager and the number of passes, as shown in Figure 16. The unit hydograph is defined for the duration specified in the paired data manager. The number of passes is meant to correct for minor inflection points in the S-curve that is used to convert the unit hydrograph from the input duration to the duration required as per the computational interval. For instance, if the unit hydrograph 3 hour duration unit hydrograph is meant to be used within a simulation that has a computational interval of 1 hour, the unit hydrograph must be converted from a 3 hour duration to a 1 hour duration. S-curves are used to perform this conversion. If the S-curves derived from the 3 hour unit hdrograph contain inflection points, the resultant 1 hour unit hydograph may display unwanted oscillations. A maximum of 20 passes is allowed. The unit hydrograph must be entered in the paired data manager before it can be selected in the Component Editor. If you wish, you can use the paired data button next to the selection list to open a chooser to assist in selecting the correct unit hydrograph.
2D Diffusion Wave Transform
The 2D Diffusion Wave transform method explicitly routes excess precipitation throughout a subbasin element using a combination of the continuity and momentum equations. Unlike unit hydrograph transform methods, this transform method can be used to simulate the non-linear movement of water throughout a subbasin when exposed to large amounts of excess precipitation (Minshall, 1960). This transform method can be combined with all Canopy, Surface, and Loss methods that are currently within HEC-HMS. However, only the None, Linear Reservoir, and Constant Monthly Baseflow methods can be used with this transform method. For instance, the Deficit and Constant Loss method can be used to convert precipitation to excess precipitation, the Simple canopy method can extract infiltrated water through evapotranspiration processes, the 2D Diffusion Wave transform method can be used to route surface flow, and the Linear Reservoir baseflow method can be used to re-introduce infiltrated water as baseflow at the subbasin outlet. Additionally, precipitation that does not initially infiltrate and becomes runoff can infiltrate at a later time or within another grid cell. Spatial variables specific to 2D, such as water surface elevation, hydraulic depth (computed as the volume of water within a cell / wetted area of the cell), and average velocity within a cell, can be displayed within the map when using this transform method.
2D Mesh
The 2D Diffusion Wave method represents the subbasin using a 2D mesh which is comprised of both grid cells and cell faces. Grid cells do not have to have a flat bottom and cell faces do not have to be straight lines with a single elevation. Instead, each grid cell and cell face is comprised of hydraulic property tables that are developed using the details of the underlying terrain. This type of model is often referred to as a “high resolution subgrid model” (Casulli, 2008). The term “subgrid” implies the use of a detailed underlying terrain (subgrid) to develop the geometric and hydraulic property tables that represent the grid cells and the cell faces. Currently, users must create a 2D mesh (and any associated connections) within HEC-RAS (version 5.0.7 or newer) and then import to HEC-HMS. In the future, users will be able to create and modify both 2D meshes and boundary conditions entirely within HEC-HMS. The 2D mesh preprocessor within HEC-RAS creates: 1) an elevation-volume relationship for each grid cell and 2) cross sectional information (e.g. elevation-wetted perimeter, area, roughness, etc) for each cell face. The net effects of using a subgrid model such as this are fewer computations, faster run times, greater stability, and improved accuracy. For more information related to the development of a 2D mesh, users are referred to the HEC-RAS 2D Modeling User's Manual.
The 2D Diffusion Wave transform can only be used with Unstructured or File-Specified Discretizations. An Unstructured Discretization can be created by importing a 2D mesh from an HEC-RAS Unsteady Plan HDF file using the File | Import | HEC-RAS HDF File... option. Unsteady Plan HDF files have extensions of ".p##.hdf" where "p##" corresponds to the specific plan of interest. When importing a 2D mesh from an HEC-RAS Unsteady Plan HDF file, any accompanying boundary conditions for the selected 2D mesh (except for precipitation time series) will be imported and used to create new 2D Connections with the same parameterization. If a File-Specified Discretization is used, the backing file must be in an HDF 5 format and created using either HEC-RAS or HEC-HMS. Pathnames to the HDF file must be limited to a maximum of 256 characters.
The 2D Diffusion Wave Component Editor is shown in Figure 17.
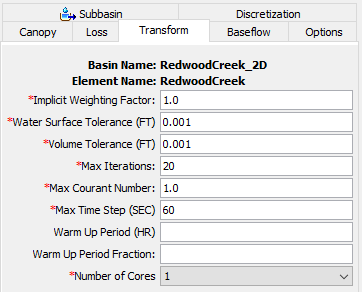
Within this component editor, users must specify various computational tolerances and parameters for the 2D mesh associated with the subbasin.
Implicit Weighting Factor
This parameter is used to weight the spatial derivatives between the current time step and the previously computed time step. In many other applications, this parameter is also termed "theta". The default value for this parameter is 1.0. However, the user can vary this parameter between 0.5 and 1.0. A value of 1.0 (which is equivalent to the Backward Euler scheme) provides the most stable solution and will use only the current time step for the spatial derivatives. A value of 0.5 (which is equivalent to the Crank-Nicholson method) provides the most accurate solution of the equations but tends to be less stable. In most applications of real world flood runoff events, a value of 1.0 will provide similar results as a value of 0.5. However, this assumption should be tested for each model due to site specific geometry and flood propagation.
Water Surface Tolerance
The water surface tolerance is used within the iteration scheme. The default value for this tolerance is 0.001. If the solution results in a numerical error that is less than the specified water surface tolerance, the solver will move to the next time step. If the solution results in a numerical error that is greater than the specified water surface tolerance, the solver will iterate over the same time step. The solver will only iterate up to the specified maximum number of iterations.
Volume Tolerance
The volume tolerance is also used within the solver for the specific 2D mesh when iterating. The default value for this tolerance is 0.001. The volume error computed by the solver is first converted to a depth using the previous time step's water surface elevation and the elevation-volume curve for the cell. Then, the change in water surface elevation is computed based on the current time step's volume error. If the solution results in a numerical error that is less than the specified volume tolerance, the solver will move to the next time step. If the solution results in a numerical error that is greater than the specified volume tolerance, the solver will iterate over the same time step. The solver will only iterate up to the specified maximum number of iterations.
Maximum Iterations
The specified maximum iterations will be used by the solver for the specific 2D mesh to get an answer that has a numerical error less than the user specified tolerances at all locations. The default value for this parameter is 20. However, the user can change it from 0 to 40. It is not recommended to change this parameter unless you are sure that changing the value will either improve the chances that the model will converge (i.e. increasing the value) or speed up the computations without causing any significant errors.
Maximum Courant Number
This option specifies the maximum Courant number that is allowed within any cell in the 2D mesh. The default value for this parameter is 1.0. If the maximum Courant number is exceeded, the computational interval will be halved for the next time step. Currently, the 2D solver used by HEC-HMS will always make use of an adaptive time step. In the future, an option to use a constant time step will be added. Because the solver uses an implicit solution scheme, Courant numbers can be greater than 1.0 and still maintain a stable and accurate solution. In general, if the flood wave is rising and falling slowly (depth and velocity are changing slowly), the solver can handle extremely high Courant numbers. For these types of cases, users may be able to enter a Courant number as high as 5.0 or more. However, if the flood wave is very rapidly changing (depth and velocity are changing very quickly over time), then a Courant number closer to 1.0 will be more appropriate.
Maximum Time Step
This option specifies the maximum time step (i.e. computational interval) that will be used within the solver for the specific 2D mesh. Currently, the 2D solver used by HEC-HMS will always make use of an adaptive time step. In the future, an option to use a constant time step will be added.
Warm Up Period
This option can be used to "ramp up" the water surface from a dry condition to a wet condition. The default value for this parameter is blank (i.e. will not be used). This option allows the user to specify a time (in hours) to run the computations for the 2D mesh while slowly transitioning any Flow 2D Connections from zero to their initial value and/or any Stage 2D Connections from a dry elevation to their initial water surface elevation. When using a warm up period, a warm up period fraction must also be specified.
Warm Up Period Fraction
This option is used in conjunction with the warm up period. The default value for this parameter is blank (i.e. will not be used). A value of 0.1 means that 10% of the specified warm up period time will be used to "ramp up" the boundary conditions to their initial values. The remaining time will be used to hold the boundary conditions constant but allow the flow to propagate throughout the 2D mesh, thus providing time to stabilize to an appropriate initial condition.
Number of Cores
This option allows users to adjust the number of cores that are used by the solver. The default value for this parameter will be set using the specified Number of Cores within the Tools | Program Settings | Defaults menu. The number of available cores will be determined for each user's computer and used to populate this drop down menu. Increasing the number of cores will result in more resources being allocated during a compute that uses the 2D Diffusion Wave transform. In general, as the number of cores is increased, the compute will proceed faster. However, there is a point of diminishing returns; increasing the number of cores past a certain point may result in decreased performance.
2D Connections
Within HEC-HMS, 2D Connections are used to supply boundary conditions as well as link other elements to/from the 2D mesh. The 2D Connection Component Editor is shown in Figure 18.
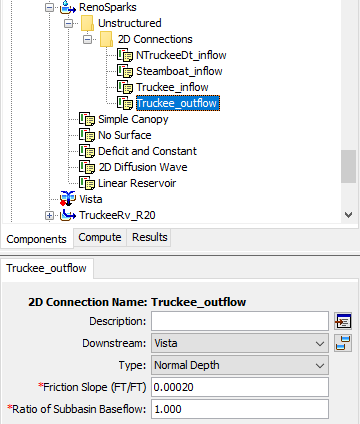
Downstream
Each 2D Connection can be connected to a downstream element through the Downstream drop down menu. However, if an upstream element (e.g. subbasin, junction, etc) is connected to a 2D Connection, the Downstream drop down will be deactivated and not editable.
Type
Four types of 2D Connections are available for use: Flow, Normal Depth, Rating Curve, and Stage. For example, if the user wanted to allow flow to leave the 2D mesh using a normal depth assumption, a Normal Depth 2D Connection could be used. Also, if the user wanted to apply a time series of flow to a 2D mesh, a Flow 2D Connection could be used. Finally, if an upstream element is connected to a 2D Connection, only the Flow or Stage type can be selected.
Stage Hydrograph
A Stage Hydrograph 2D Connection allows the user to supply flow or allow flow to leave a 2D mesh. If the water surface elevation supplied by the 2D Connection is higher than the cell water surface elevation (or dry elevation), flow will go into the cell. When the water surface elevation supplied by the 2D Connection is lower than the cell water surface elevation, flow will leave the cell. If a cell is dry and the water surface elevation supplied by the 2D Connection is lower than the cell minimum elevation, no flow will transfer. Flow is computed on a per cell basis. For instance, if the water surface elevation supplied by the 2D Connection is higher in some of the connected cells but lower in other connected cells, water will simultaneously enter and exit the Stage Hydrograph boundary.
When using this type of connection and an upstream element is not connected, a time series of stage must be supplied.
When the Initial Stage option is set to Yes, the first stage in the associated hydrograph will be used to fill the 2D mesh as an initial condition. The filling starts at the 2D Connection and proceeds to fill any cell as long as it is hydraulically connected. The filling stops when faces with a higher elevation are encountered that is higher than the initial stage.
Flow Hydrograph
A Flow Hydrograph 2D Connection is generally used to supply flow into a 2D mesh. However, this type can also be used to remove flow from a 2D mesh by using negative flow values.
When using this type of connection and an upstream element is not connected, a time series of flow must be supplied.
The Energy Grade Slope is used to compute a normal depth from the given flow rate and the underlying terrain data along the 2D Connection for each computational time step. This slope should be estimated at the location of the 2D Connection. A flow distribution along the 2D Connection is then computed based on the normal depth water surface elevation and the conveyance. The flow distribution is then used to appropriately distribute the flow to cells along the 2D Connection that are wet. At any given time step, only a portion of the 2D Connection may be wet, thus only the cells in which the water surface elevation is higher than their outer boundary face terrain will receive water. However, if the computed normal depth water surface elevation is higher than all the boundary face elevation data along the 2D Connection, then all the cells will receive water based on a conveyance weighting approach.
Normal Depth
A Normal Depth 2D Connection can only be used to allow flow to leave a 2D mesh.
The Friction Slope is used to compute a normal depth water surface elevation given the underlying terrain data along the 2D Connection for each computational time step. This slope should be estimated at the location of the 2D Connection. Similar to a Stage Hydrograph 2D Connection, a Normal Depth 2D Connection is applied on a per cell basis.
Rating Curve
A Rating Curve 2D Connection can only be used to allow flow to leave a 2D mesh. Similar to a Stage Hydrograph 2D Connection, a Rating Curve 2D Connection is applied on a per cell basis.
Ratio of Subbasin Baseflow
The Ratio of Subbasin Baseflow is defined as the ratio of baseflow generated within the subbasin that will reach the particular 2D Connection. The default value for this parameter is 0.0, which implies that no baseflow generated within the subbasin will reach the particular 2D Connection. Conversely, a value of 1.0 implies that all baseflow generated within the subbasin will reach the particular 2D Connection. This parameter cannot be used to remove or create mass within a subbasin; as such, the ratios of subbasin baseflow for all 2D Connection in a particular 2D mesh or subbasin must sum to 1.0. However, when the None baseflow method is selected for a subbasin, no checks regarding this parameter will be performed.