Download PDF
Download page Optimization Trials.
Optimization Trials
Parameter estimation is the process of adapting a general model to a specific watershed. Some parameters can be estimated directly from field measurements. For example, the area that must be entered for a Subbasin Element can be measured directly in the field using standard surveying procedures or from maps developed through surveying. Other parameters can be estimated indirectly from field measurements. In this case, the field measurement does not result in a value that can be input directly to the program. However, the field measurement can provide a strong recommendation for a parameter in the program based on previous experience. For example, measurements of soil texture are correlated with parameters such as hydraulic conductivity. Finally, there are parameters that can only be estimated by comparing computed results to observations such as measured streamflow or snow water equivalent. Even for parameters of the first two types, there is often enough uncertainty in the true parameter value to require some adjustment of the estimates in order for the model to closely follow the observed data.
The quantitative measure of the goodness-of-fit between the computed result from the model and the observed data is called the Objective Function. Different Objective Functions measure the degree of variation between computed and observed hydrographs in different ways. Some functions report a value that decreases as the agreement between simulated and observed increases, and some do the opposite, increasing as goodness-of-fit increases. The key to automated parameter estimation is a search method for adjusting parameters to direct the Objective Function value towards better goodness-of-fit, and find optimal parameter values. An optimal value for the Objective Function is obtained when the parameter values best able to reproduce the observed hydrograph are found. Constraints are set to ensure that unreasonable parameter values are not used.
Optimization Trials are one of the components that can compute results. Each trial is composed of a Basin Model, Meteorologic Model, and Time Control Information. The trial also includes selections for the Objective Function, Search Method, and Parameters to be adjusted in order to find an optimal model. A variety of result graphs and tables are available from the Watershed Explorer for evaluating the quality of the results.
The iterative parameter estimation procedure used by the program is often called Optimization. Initial values for all parameters are required at the start of the Optimization Trial Time Window. A hydrograph is computed at a target element by computing all of the upstream elements. The target must have an observed hydrograph for the time period over which the Objective Function will be evaluated. Only parameters for upstream elements can be estimated. The value of the Objective Function is computed at the target element using the computed and observed hydrographs. Parameter values are adjusted by the search method and the hydrograph and Objective Function for the target element are recomputed. This process is repeated until the value of the Objective Function is sufficiently small, or the maximum number of iterations is reached. Results can be viewed after the Optimization Trial is complete.
Creating a New Optimization Trial
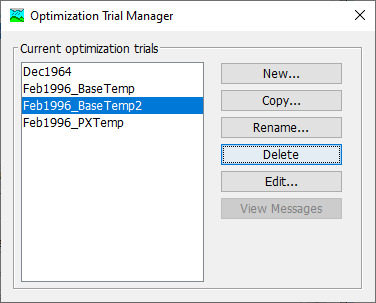
A new Optimization Trial is created using a wizard that helps you navigate the steps to creating a new trial. There are two ways to access the wizard. The first way to access the wizard is to click on the Compute menu and select the Create Compute | Optimization Trial command; it is only enabled if at least one Basin Model and Meteorologic Model exist. The wizard will open and begin the process of creating a new Optimization Trial. The second way to access the wizard is from the Optimization Trial Manager. Click on the Compute menu and select the Optimization Trial Manager command. The Optimization Trial Manager will open and show any trials that already exist. Press the New button to access the wizard and begin the process of creating an Optimization Trial, as shown below.
The first step of creating an Optimization Trial is to provide the name for the new trial (shown below). A default name is provided for the new Optimization Trial; you can use the default or replace it with your own choice. After you finish creating the trial you can add a description to it. If you change your mind and do not want to create a new Optimization Trial, you can press the Cancel button at the bottom of the wizard or the X button in the upper right corner of the wizard. The Cancel button can be pressed at any time you are using the wizard. Press the Next button when you are satisfied with the name you have entered and are ready to proceed to the next step.

The second step of creating an Optimization Trial is to select a Basin Model. All of the Basin Models that are currently part of the project are displayed in alphabetical order. By default the first Basin Model in the table is selected. The selected Basin Model is highlighted. You can use your mouse to select a different Basin Model by clicking on it in the table of available choices. You can also use the arrow keys on your keyboard to select a different Basin Model. Press the Next button when you are satisfied with the Basin Model you have selected and are ready to proceed to the next step. Press the Back button if you wish to return to the previous step and change the name for the new Optimization Trial.
The third step of creating an Optimization Trial is to select a Meteorologic Model. All of the Meteorologic Models that are currently part of the project are displayed in alphabetical order. By default the first Meteorologic Model in the table is selected. The selected Meteorologic Model is highlighted. You can use your mouse to select a different Meteorologic Model by clicking on it in the table of available choices. You can also use the arrow keys on your keyboard to select a different Meteorologic Model. You are responsible for selecting a Basin Model in step 2 and a Meteorologic Model in this step that will successfully combine to compute results. Press the Back button if you wish to return to the previous step and select a different Basin Model. Press the Finish button when you are satisfied with the name you have entered, the Basin Model and element you selected, the Meteorologic Model you selected, and are ready to create the Optimization Trial.
Copying an Optimization Trial
There are two ways to copy an Optimization Trial. Both methods for copying a trial create an exact duplicate with a different name. Once the copy has been made it is independent of the original and they do not interact.
The first way to create a copy is to use the Optimization Trial Manager, which is accessed from the Compute menu. Select the Optimization Trial you wish to copy by clicking on it in the list of current Optimization Trials. The selected trial is highlighted after you select it. After you select a trial you can press the Copy button on the right side of the window. You can enter a new name and description of the copy in the Copy Optimization Trial window. A default name is provided for the copy; you can use the default or replace it with your own choice. A description can also be entered; if it is long you can use the button to the right of the description field to open an editor. When you are satisfied with the name and description, press the Copy button to finish the process of copying the selected Optimization Trial. You cannot press the Copy button if no name is specified. If you change your mind and do not want to copy the selected Optimization Trial, press the Cancel button or the X button in the upper right to return to the Optimization Trial Manager window.
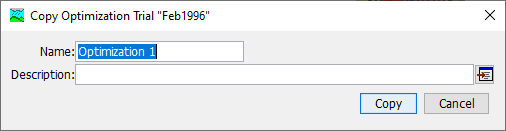
The second way to copy is from the Compute tab of the Watershed Explorer. Move the mouse over the Optimization Trial you wish to copy and press the right mouse button (shown below). A context menu is displayed that contains several choices including copy. Click the Create Copy command. The Copy Optimization Trial window will open where you can name and describe the copy that will be created. A default name is provided for the copy; you can use the default or replace it with your own choice. A description can also be entered; if it is long you can use the button to the right of the description field to open an editor. When you are satisfied with the name and description, press the Copy button to finish the process of copying the selected Optimization Trial. You cannot press the Copy button if no name is specified. If you change your mind and do not want to copy the selected Optimization Trial, press the Cancel button or the X button in the upper right of the Copy Optimization Trial window to return to the Watershed Explorer.

Renaming an Optimization Trial
There are two ways to rename an Optimization Trial. Both methods for renaming a trial change its name and perform other necessary operations.
The first way to perform a rename is to use the Optimization Trial Manager, which you can access from the Compute menu. Select the Optimization Trial you wish to rename by clicking on it in the list of current Optimization Trials. The selected trial is highlighted after you select it. After you select a trial you can press the Rename button on the right side of the window. The Rename Optimization Trial window (shown below) will open where you can provide the new name. If you wish you can also change the description at the same time. If the new description will be long, you can use the button to the right of the description field to open an editor. When you are satisfied with the name and description, press the Rename button to finish the process of renaming the selected Optimization Trial. You cannot press the Rename button if no name is specified. If you change your mind and do not want to rename the selected simulation trial, press the Cancel button or the X button in the upper right of the Rename Optimization Trial window to return to the Optimization Trial Manager window.

The second way to rename is from the Compute tab of the Watershed Explorer. Select the Optimization Trial you wish to rename by clicking on it in the Watershed Explorer; it will become highlighted. Keep the mouse over the selected trial and click the left mouse button again. The highlighted name will change to editing mode (shown below). You can then move the cursor with the arrow keys on the keyboard or by clicking with the mouse. You can also use the mouse to select some or all of the name. Change the name by typing with the keyboard. When you have finished changing the name, press the Enter key to finalize your choice. You can also finalize your choice by clicking elsewhere on the Compute tab. If you change your mind while in editing mode and do not want to rename the selected Optimization Trial, press the Escape key.

Deleting an Optimization Trial
There are two ways to delete an Optimization Trial. Both methods for deleting a trial remove it from the project and automatically delete previously computed results. Once a trial has been deleted it cannot be retrieved or undeleted.
The first way to perform a deletion is to use the Optimization Trial Manager, which you can access from the Compute menu. Select the Optimization Trial you wish to delete by clicking on it in the list of current Optimization Trials. The selected trial is highlighted after you select it. After you select a trial you can press the Delete button on the right side of the window. A window will open where you must confirm that you wish to delete the selected trial as shown below. Press the OK button to delete the trial. If you change your mind and do not want to delete the selected Optimization Trial, press the Cancel button or the X button in the upper right to return to the Optimization Trial Manager window.
The second way to delete is from the Compute tab of the Watershed Explorer. Select the Optimization Trial you wish to delete by clicking on it in the Watershed Explorer; it will become highlighted (shown below). Keep the mouse over the selected trial and click the right mouse button. A context menu is displayed that contains several choices including delete. Click the Delete command. A window will open where you must confirm that you wish to delete the selected trial. Press the OK button to delete the trial. If you change your mind and do not want to delete the selected Optimization Trial, press the Cancel button or the X button in the upper right to return to the Watershed Explorer.

Selecting Components
One of the principal tasks when creating an Optimization Trial using the wizard is the selection of the components that will be used to compute optimization results. The components include the Basin Model and the Hydrologic Element in the Basin Model where the Objective Function will be computed. The components also include the Meteorologic Model. These components are selected when creating a new Optimization Trial with the wizard. However, you can change the Basin Model and Meteorologic Model you wish to use at any time using the Component Editor for the Optimization Trial. Access the Component Editor from the Compute tab of the Watershed Explorer (shown below). If necessary, click on the Optimization Trials folder to expand it and view the available Optimization Trials. The Component Editor contains a Basin Model selection list that includes all of the Basin Models in the project where the Basin Model has at least one element with observed data. The Component Editor also contains a Meteorologic Model selection list that includes all of the Meteorologic Models in the project. The Search and Objective tabs of the Optimization Trial Component Editor are discuss in the following sections.
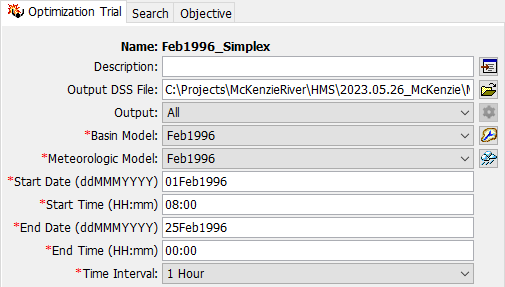
Entering a Time Window
You must enter a Start Date and Time and an End Date and Time for the Optimization Trial. The time control information is not specified in the wizard used to create the Optimization Trial. The time control information must be entered after the trial is created using the Component Editor for the Optimization Trial (shown above). Enter the start date using the indicated format for numeric day, abbreviated month, and four-digit year. Enter the end date using the same format. The start time and end time are entered using 24-hour time format. Choose a time interval from the available options which range from 1 minute up to 1 day. The start time and end time must each be an integer number of time intervals after the beginning of the day.
Search Methods: Deterministic
Two Deterministic Search Methods are available for optimizing the Objective Function and returning optimal parameter values: Univariate Method and Simplex Method. The Univariate Method evaluates and adjusts one parameter during the optimization simulation, the user can choose only one parameter for the program to adjust when the Univariate Method is selected. The Simplex Method uses a downhill simplex to evaluate all parameters simultaneously and determine which parameter to adjust. The default method is the Simplex Method. When the Simplex Method is specified, at least two parameters must be selected.
Selecting the Search Method for the Optimization Trial is accessed from the Compute tab of the Watershed Explorer in the Optimization Trial Component Editor. Click on the Optimization Trial node to display the Component Editor for the Optimization Trial. If necessary, click on the Optimization Trials folder to expand it and view the available Optimization Trials in the project.
Two methods are provided for controlling the search process, the Univariate or Simplex methods. Both search methods function by iteratively adjusting parameter values to decrease the Objective Function value (increase if the goal is maximization); each parameter adjustment is termed an Iteration. The Tolerance determines the change in the Objective Function value between two successive iterations that will terminate the search.
Two Tolerance Criterion types, Absolute and Relative, are available for use with the Simplex Method. Convergence is assessed based on specified tolerance and tolerance type. When an Absolute criterion is selected, convergence is assessed based on the absolute tolerance, or the absolute difference between the nodes of the Simplex. This means that the magnitude of the Objective Function affects the determination of convergence. For example, a larger tolerance is needed for the Sum of Squared Errors (SSE) Objective Function than for the Root Mean Square Error (RMSE) Objective Function for the trial to converge in a similar number of iterations because values of the SSE function are generally orders of magnitude larger than for RMSE. When the Relative criterion is selected, convergence is assessed based on the relative tolerance, or the relative difference between the nodes of the Simplex. The Relative criterion is less sensitive to the magnitude of the Objective Function values. In general, the Relative criterion is preferred, but the default option is Absolute for backwards compatibility.
The Maximum Number of Iterations also can be used to limit the search. The search will stop when the maximum number of iterations is reached regardless of changes in the Objective Function value or the quality of the estimated parameters. The tolerance and maximum iterations are both entered on the Search tab within the Optimization Trial Component Editor. Defaults are provided for both criteria. The initial default values depend on the selected search method.

Search Methods: Stochastic
Two Stochastic Search Methods are available: Differential Evolution and Markov Chain Monte Carlo. However, the Markov Chain Monte Carlo option has been turned off in the HEC-HMS user interface.
The Differential Evolution (DE) Search Method behaves similarly to the Simplex Search Method; however, Iterations of the search vary the parameters at random instead of in a deterministic way. This means that two DE searches set up in an identical way may proceed in different ways, and reach convergence in a different amount of time. However, any DE search will settle on a single optimal parameter set based on the selected Objective Function and time series. The figure below shows the search configured using the DE method.
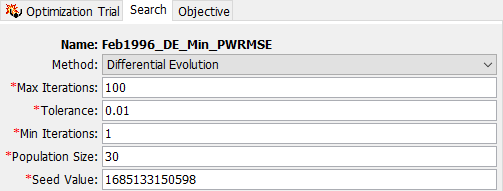
DE has three additional parameters beyond the two required for Simplex. The Population Size controls the number of parameter sets (and therefore model evaluations) that occur in each iteration. The default value of 30 is typically a good choice for hydrologic modeling applications. Using too few population members makes it more difficult to assess convergence, and using too many makes the search take longer. When there are a large number of parameters, or the problem is particularly complex, a higher value for Population Size may help the search find the global optimum. The Seed Value initializes the pseudorandom number generator that creates the parameter random samples in the search. A search with the same seed will always produce the same random numbers, so two DE searches with the same settings and seed will always produce the same results. The seed value is initialized by the system clock when a new DE search is created. The Min Iterations setting requires the search to complete a minimum number of iterations before assessing convergence. This can be used in conjunction with the Tolerance setting to achieve the desired result. The Tolerance value of 0.01 is a good value to start with; however, if you find that there is still a notable variability in the parameter traces in a converged trial, a smaller value may be required, or, use a higher value for Min Iterations. Using too small of a value for Tolerance will increase the search time without substantially improving parameter estimates. Using too large of a value will result in false convergence.
Tolerance Setting
Each of the three search methods, Univariate, Simplex, and Differential Evolution, assess search convergence in different ways. The Tolerance Setting is treated differently for each of these three methods. Additionally, using different Objective Functions or applying a data transformation may affect the rate of convergence due to the magnitude of the computed Objective Function. Decreasing the tolerance setting will require additional iterations of the search to be run and potentially increase the Optimization Trial run time. However, a smaller tolerance value will result in parameter estimates that are closer to the Objective Function goal with higher certainty.
Markov Chain Monte Carlo (MCMC) is the stochastic search method available in HEC-HMS. The general principle of MCMC optimization is this: the algorithm seeks to visit the plausible parameter sets in a parameter space by a random walk, and visit parameter sets that are more likely to have created the observed dataset more often. MCMC search proceeds by generating a sequence of parameter values by making random transitions from one state of a Markov Chain to another using a proposal distribution. Each state is a set of model parameter values for the parameters being optimized. If the present state (parameter values) of the Markov Chain implies good agreement between the simulated and observed data, then the iteration is less likely to make large jumps away from the present state. This produces repeated samples from a region of the parameter space that is associated with higher likelihood that the parameter set produced the observed values. If the agreement is not good, then larger random leaps across the parameter space are likely to occur. Multiple chains, which are initialized with different starting conditions, are used to assess whether the samples have escaped the starting conditions and have begun to draw samples from the highest-likelihood regions of the parameter space, which are unknown at the outset. The state of drawing from the highest-likelihood region of the parameter space is called Equilibrium. It is desirable to have many samples from this region in order to characterize the statistical properties of the parameters associated with this high-likelihood space.
The MCMC Search requires additional parameterization in order to operate (shown below). Pool Size controls the number of independent Markov Chains used in the simulation. Initial Sample controls the number of burn-in samples to be taken before beginning to assess sample convergence. Min Iterations and Max Iterations controls the allowable range of iterations for the simulation. Convergence allows the user to set the value for the Gelman-Rubin statistic that discriminates between pre- and post-equilibrium samples (the default value of 1.2 is generally sufficient; higher discrimination would be enforced using a lower number not lower than 1.0). Equilibrium Sample controls the number of samples drawn after the simulation has achieved a state of equilibrium.
Selecting the Search Method for the Optimization Trial is accessed from the Compute tab of the Watershed Explorer in the Optimization Trial Component Editor. Click on the Optimization Trial node to display the Component Editor for the Optimization Trial. If necessary, click on the Optimization Trials folder to expand it and view the available Optimization Trials in the project.

Objective Function: Univariate, Simplex, and Differential Evolution
The Objective Function measures the goodness-of-fit between the computed results and observed data at the selected element. For the Minimization Goal, there are fourteen different goodness-of-fit functions which decrease as agreement between simulated and observed increases. The Maximization Goal can be used in two different ways: to Maximize an Element Property such as flow volume or peak discharge, reservoir stage, etc., or to Maximize a Goodness-of-Fit Statistic which increases in value as goodness-of-fit increases. See the following table for Minimization Goal Objective Functions and the subsequent table for Maximization Goal Objective Functions.
Objective Function | Motivation |
|---|---|
First Lag Autocorrelation | Minimize systematic bias in residuals |
Maximum of Absolute Residuals | Minimize the largest single distance between observed and simulated |
Maximum of Squared Residuals | Minimize the largest single distance between observed and simulated |
Mean of Absolute Residuals | Minimize the average distance between observed and simulated |
Mean of Squared Residuals | Minimize the average distance between observed and simulated, with larger weight to larger errors |
Peak-Weighted RMSE | Minimize the average distance between observed and simulated, with larger weight to data greater than the mean |
Percent Error in Peak Discharge | Minimize the difference between observed and simulated peak discharge value |
Root Mean Square Error | Minimize the average distance between observed and simulated, with larger weight to larger errors; a classical choice |
Sum of Absolute Residuals | Minimize the average distance between observed and simulated |
Sum of Squared Residuals | Minimize the average distance between observed and simulated, with larger weight to larger errors |
Time-Weighted RMSE | Minimize the average distance between observed and simulated, with larger weight to data near the end of the time window |
Variance of Absolute Residuals | Minimize the variation in residual values |
Variance of Squared Residuals | Minimize the variation in residual values, with larger weight to larger residual values |
Objective Function | Motivation |
|---|---|
Coefficient of Determination | Maximizes explained variance in observed data. Also called R2. |
Discharge Volume | Maximizes the total volume discharged over the Objective Function time window. |
Index of Agreement | Maximizes the dimensionless Index of Agreement statistic. |
Modified Kling-Gupta Efficiency | Maximizes the dimensionless Modified Kling-Gupta Efficiency statistic. |
Nash Sutcliffe | Maximizes the dimensionless Nash-Sutcliffe Efficiency statistic. |
Peak Discharge | Maximizes the single maximum discharge over the Objective Function time window. |
Peak Elevation | Reservoir element only. Maximizes the single maximum reservoir elevation over the Objective Function time window. |
Relative Index of Agreement | Maximizes the dimensionless Index of Agreement statistic with less weight to large values |
Relative Nash Sutcliffe | Maximizes the dimensionless Nash Sutcliffe Efficiency statistic with less weight to large values |
Maximization of an Element Time-Series Statistic, such as flow volume, peak discharge, or especially peak reservoir pool elevation, is used in conjunction with hazard analyses such as those required for dam safety studies. A particularly important optimization is when the trial is used in conjunction with the HMR 52 Storm Precipitation Method to maximize a statistic. The Optimization Trial automatically adjusts HMR 52 Storm parameters during the maximization trial, which replaces the need for many manual iterations of running simulations to determine the optimal HMR52 Storm Parameter Set.
The figure below shows the Objective tab for the Optimization Trial Component Editor. Maximization is set for the Goal of the optimization. The Location is the Basin Model Element where the user wants the Optimization Trial to maximize the selected statistic. Any element within the Basin Model can be selected. The Time-Series drop down list provides options based on the type of element selected for the location. If a reach, subbasin, or junction is selected, then discharge is the only available time-series. If a reservoir element is selected, then the user can choose between discharge and pool elevation. The Statistic is the computed result that is maximized during the Optimization Trial. When Discharge is selected as the time-series, then the user can choose a statistic of Discharge Volume or Peak Discharge. When Pool Elevation is selected as the time-series, then the only statistic option is Peak Elevation.

The HMR 52 Storm Parameters that can be adjusted in the Optimization Trial are Orientation, Area, X and Y Coordinates, and the Peak Intensity Period. The figure below shows the the Parameter tab within the Optimization Trial Component Editor. The Precipitation Parameters option is chosen for the Element (the precipitation parameters are global to all subbasins in the Basin Model). The parameter list includes all parameter available to be adjusted during the Optimization Trial. The initial value is the value specified in the Meteorologic Model referenced by the Optimization Trial but the user can change the initial value. Default minimum and maximum values are set by the program. The user should override these values with information about the watershed. By default, the minimum and maximum x and y coordinates are defined using coordinates from the subbasin GIS features.

Select the Objective Function Method for the Optimization Trial on the Component Editor for the Objective Function (shown below). Access the Component Editor from the Compute tab of the Watershed Explorer. If necessary, click on the Optimization Trials folder to expand it and view the available Optimization Trials in the project. Click on the Optimization Trial node to expand it and see the Objective Function node. Click on the Objective Function node to view the editor. Select the Objective tab within the Component Editor.
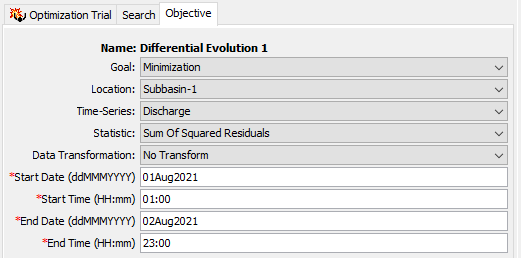
An Element with Observed Data was selected at the time the Optimization Trial was created. This is the location where the Objective Function will be evaluated. You can change the element location at any time using the Component Editor for the Objective Function. The selection list shows all of the elements with observed flow and/or snow water equivalent in the Basin Model selected for the Optimization Trial. Select a different element in the list to change where the Objective Function will be evaluated. Recognize that parameters can only be estimated at locations upstream of the selected element. Changing the location will change which parameters can be estimated. In general, the observed data record at the selected element location should not contain any missing data.
The Objective Function is evaluated over a Specified Time Window. The time window cannot begin before the start time of the Optimization Trial. Also, the time window cannot end after the end time of the Optimization Trial. However, you have the option of changing the time window to be narrower than the one specified for the whole Optimization Trial. By default, the start and end time for the Objective Function will default to the time window of the Optimization Trial.
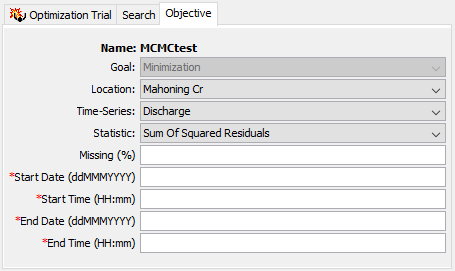
Objective Function: Markov Chain Monte Carlo
Only one Goal and Objective Function are available for MCMC Optimization: Minimization Goal with the Sum of Squared Residuals Objective Function. This combination allows the MCMC algorithm to assess the likelihood that a particular parameter set is the one that produced the observed data. The figure below shows this selection, which is populated by default when MCMC is selected.
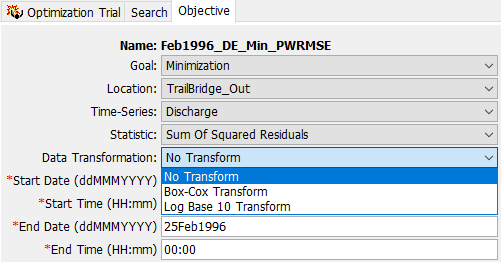
Data Transformations
Three options are available for Data Transformations: No Transformation, Log Base 10, and Box-Cox. The transform is applied both to the observed and simulated time series before the Objective Function is computed. This will change the magnitude of the Objective Function in many cases. The figure below shows the selection menu for data transformations. Both the Log Base 10 and Box-Cox transformation methods require that the data being transformed are positive, so a Shift is applied in both cases to ensure that all data are positive. This shift is automatically estimated. The Power parameter for the Box-Cox transform is also automatically estimated using the method of maximum likelihood. If there are missing observed data in the Objective Function time window, the transformation parameter(s) cannot be estimated, and the search will default to the No Transform option.
Adding and Deleting Parameters
The parameters that will be automatically estimated must be at the selected element location or upstream of it in the element network. When the selected location is changed, elements will be automatically deleted if they are not upstream of the newly selected location. Parameters that can be chosen for estimation are a selected set of the Canopy, Surface, Loss Rate, Transform, Baseflow Parameters in the Subbasin, Routing Parameters in the Reach, and Snowmelt Parameters. Parameters that should be strictly measured in the field are not allowed to be estimated. For example, it is not permissible to estimate subbasin area or a reach length.
Care must be taken when selecting parameters for estimation. While it is possible to select the same parameter more than once, it is not recommended. In this scenario, the search method attempts to improve estimates by adjusting the same parameter value at different and sometimes conflicting points in the search. This can lead to a so-called blocking condition where the search method cannot accurately determine how to adjust parameters to improve the Objective Function and less than optimal results are achieved.
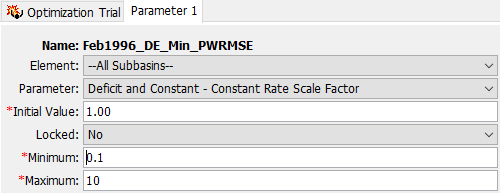
Care must also be taken when selecting parameters at elements upstream of the observed data location. It is possible to select multiple parameters that have similar affects on the computed hydrograph at the evaluation location. In this case, adjustments to one parameter can off set adjustments in others. For example, estimates of the time of concentration at multiple subbasins upstream of the evaluation location often result in poor results. Special parameters called Scale Factors have been included that adjust all similar parameters upstream of the evaluation location together in the same direction. However, care is still required even with this special scaling. Scale factors can be used specifying the optimization location at a downstream location from the elements to be scaled (e.g. a junction), adding a parameter, and selecting All Subbasins as the element of interest. Then, the parameter entry will allow for selection of scale factors, as shown below.
Add a new parameter to an Optimization Trial using the Watershed Explorer. Move the mouse over the Optimization Trial and press the right mouse button (shown below). A context menu is displayed that contains several choices including adding a parameter. Click the Add Parameter command. If you are using the Univariate Search Method and a parameter has already been added to the Optimization Trial, additional parameters will not be added. The following collection of tables show Subbasin Canopy Parameters, Subbasin Surface Parameters, Loss Rate Parameters, Subbasin Transform Parameters, Baseflow Parameters, Reach Routing Parameters, and Snowmelt Parameters that can be added.

Delete a parameter from an Optimization Trial using the Watershed Explorer. Select the parameter you wish to delete by clicking on it in the Watershed Explorer; it will become highlighted. Keep the mouse over the selected parameter and click the right mouse button (shown below). A context menu is displayed that contains several choices including deleting a parameter. Click the Delete Parameter command.

Method | Parameter |
|---|---|
Dynamic | Initial Storage |
Maximum Storage | |
Gridded Simple | Initial Storage |
Simple | Initial Storage |
Maximum Storage | |
| Crop Coefficient |
Method | Parameter |
|---|---|
Gridded Simple | Initial Storage |
Simple | Initial Storage |
Maximum Storage | |
Dynamic | Initial Storage |
Maximum Storage |
Method | Parameter |
|---|---|
Curve Number | Initial Abstraction |
Constant Rate | |
Deficit Constant | Initial Deficit |
Maximum Deficit | |
Constant Rate | |
Exponential | Initial Range |
Initial Coefficient | |
Coefficient Ratio | |
Exponent | |
Green Ampt | Initial Content |
Saturated Content | |
Suction | |
Conductivity | |
Gridded Curve Number | Initial Abstraction Ratio |
Potential Retention Scale Factor | |
Gridded Deficit Constant | Initial Deficit Ratio |
Maximum Deficit Ratio | |
Constant Rate Ratio | |
Impervious Area Ratio | |
Gridded SMA | Soil Initial Storage |
Groundwater 1 and 2 Initial Storage | |
Initial Constant | Initial Loss |
Constant Rate | |
Smith Parlange | Initial Content |
Residual Content | |
Saturated Content | |
Bubbling Pressure | |
Pore Distribution | |
Conductivity | |
Beta Zero | |
Soil Moisture Accounting | Soil Initial Storage |
Soil Storage | |
Soil Tension Storage | |
Soil Percolation | |
Groundwater 1 and 2 Initial Storage |
Method | Parameter |
|---|---|
Clark | Time of Concentration |
Storage Coefficient | |
Kinematic Wave | Plane Roughness |
Subcollector, Collector, and | |
ModClark | Time of Concentration |
Storage Coefficient | |
SCS | Time Lag |
S-Graph | Time Lag |
Snyder | Peaking Coefficient |
Standard Lag |
Method | Parameter |
|---|---|
Bounded Recession | Initial Flow Rate or Initial Flow Rate per Area 1 |
Recession Constant | |
Linear Reservoir | Initial Flow Rate or |
Storage Coefficient | |
Number of Reservoirs / Steps | |
Nonlinear Boussinesq | Initial Flow Rate or Initial Flow Rate per Area 1 |
Characteristic Length | |
Hydraulic Conductivity | |
Drainable Porosity | |
Threshold Ratio or Threshold Flow Rate 2 | |
Recession | Initial Flow Rate or Initial Flow Rate per Area 1 |
Recession Constant | |
Threshold Ratio or Threshold Flow Rate 2 |
1 The available parameter depends on the method selected for specifying the initial condition.
2 The available parameter depends on the method selected for specifying the recession threshold.
Method | Parameter |
|---|---|
Kinematic Wave | Manning's n |
Lag | Lag |
Modified Puls | Subreaches |
Initial Flow | |
Muskingum | K |
X | |
Subreaches | |
Muskingum Cunge | Manning's n |
Straddle Stager | Lag |
Duration |
| Method | Parameter |
|---|---|
| Temperature Index | PX Temperature |
| Base Temperature | |
| Wet Meltrate * | |
| Rain Rate Limit | |
| ATI-Meltrate Coefficient | |
| Dry Meltrate * | |
| Cold Limit | |
| ATI-Coldrate Coefficient | |
| Liquid Water Capacity | |
| Ground Melt Rate | |
| Hybrid | Rain Threshold Temperature |
Snow Threshold Temperature | |
| Base Temperature | |
| Melt Factor | |
| Max Negative Melt Factor | |
ATI Coefficient | |
Wind Function | |
| Liquid Water Capacity | |
| Energy Budget | Rain Threshold Temperature |
Snow Threshold Temperature | |
| New Snow Albedo | |
| Minimum Snow Albedo | |
| Albedo Refresh Depth | |
Albedo Decay Coefficient | |
Snow Thermal Conductivity | |
| Snow Capillary Retention | |
| Snow Hydraulic Conductivity | |
| Effective Thermal Ground Depth |
* Only Constant Value parameter types can currently be optimized
Specifying Parameter Information
A variety of information must be specified for each Optimization Parameter in order for the search method to function. Select the parameter you wish to edit by clicking on it in the Watershed Explorer. Click on the Optimization Trial node to expand it. The first node under the Optimization Trial will be the Objective Function. Following the Objective Function will be a separate node for each parameter. Click on the desired node in the Watershed Explorer to view the Component Editor for the optimization.
Each optimization parameter must select the Element where the desired parameter resides. All eligible subbasin and reach elements upstream of the Objective Function evaluation location are shown in the selection list. Eligible subbasins are those using the methods listed in the previous tables showing available parameters. Eligible reaches are those using the methods listed in the Reach Routing Parameters available for optimization table. Choosing an element from the list will update the list of available parameters based on the methods in use at that selected element. You may also have the choice of selecting the All Subbasins option in order to apply Scale Factors.
Each optimization parameter must select a specific Parameter for the chosen element. The available choices are shown in the selection list. Once you make a choice from the list, the remainder of the data in the Component Editor will become available for use (shown below).
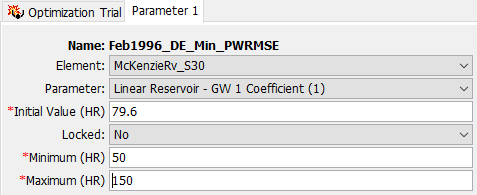
The Initial Value is the starting point for the parameter estimation process. The search method will begin searching from that point for optimal parameter values. The default initial value is the parameter value in the Basin Model that was selected for the Optimization Trial. You may change the initial value without affecting the Basin Model.
Default Minimum and Maximum Values
The Minimum and Maximum values initially provided are the maximum allowed parameter range in HMS. Do not use this range in a search. Any minimum and maximum value you provide must be inside of this default range, but this initial range is far too wide for a successful search. A narrow search range is much more likely to identify an optimal solution in a smaller number of iterations than a wide one. The search methods are not always successful at traversing very wide search ranges.
It is possible to Lock a parameter. When a parameter is locked, the initial value is used and no adjustments are made during the search process.
The Minimum parameter value can be used to narrow the lower end of the range of values that will be used by the search method. Likewise, the Maximum parameter value can be used to narrow the upper end of the range of values that will be used by the search method. A good source of information for narrowing the search range is preliminary estimates from field measurements or manual calibration. Default values for the minimum and maximum are provided based on physical and numerical limits. The search may continue outside the specified range. When it does so, a Penalty is applied to the Objective Function that is an exponential function of the distance outside the specified range. The penalty nudges the search for optimal parameter values back to the range between the specified minimum and maximum.
Parameter Ranges
The specified Parameter Ranges are not hard limits, and the search can potentially explore parameter values outside of the range. The Penalty Function is a smooth continuous function in order to prevent instabilities or issues with the solver, and the penalty factor can be small depending on the magnitude of the parameter, the Objective Function, and other factors. If the optimum parameter value is outside of the user specified range, and the improvement in the Objective Function overcomes the magnitude of the penalty function, then the Trial will return parameter values that are outside of the user specified range. This is an indication that the user should carefully evaluate their parameter ranges, and potentially which parameters are involved in the Optimization Trial.
Simplex Search Pro Tips
- No Optimization Search Method is perfect - it is limited by the complexity of the problem, the sensitivity of the parameters you are optimizing, and the choice of initial guess and parameter ranges you assign. The Nelder-Mead Simplex Search is efficient when the problem is well-defined, but can become inefficient quickly with too many parameters, poor initial guesses, and search ranges that are too large.
- The more parameters that you include in your search, the worse the performance of the search. This is mainly due to the Curse of Dimensionality.
- Pick a meaningful Parameter Range and Initial Guess for your search. The best way to speed up the search is to pick a small but meaningful range for each parameter. The next best way is to provide a good initial guess. The search takes both into account at the beginning of the trial.
- Avoid optimizing Initial Conditions if you can. If you add them as optimization parameters, consider locking them and setting them yourself to improve the search.
- If you don't like your results the first time and think the search can do better, back-feed your optimized parameters as initial guesses in the same search setup. The initial guesses are important. Also consider reducing your tolerance, increasing the maximum number of iterations, changing the Objective Function, and/or changing the time window where the Objective Function are evaluated.
- Unfortunately, the Order of the parameters matters because it influences the initial setup of the problem. If you are getting answers that don't make sense, consider changing the order of the parameters in your search. The initial Simplex does its best to span each parameter range but each parameter might not be equally dispersed in the initial state. Simplex is really constrained in that it can only compare n+1 parameter values (where n is the number of parameters) at any time, so choosing the parameter ranges well is crucial.
- If you are performing a Maximization Goal Search (e.g. maximizing peak discharge or discharge volume), choose initial values close to the boundary that are likely to maximize the search. For example, choose an initial value for constant loss rate that is close to the lower bound.
- If you are using optimization to inform your model calibration, the Optimization Trials may still be iterative in the same way as a manual calibration. You will want to adjust initial values, parameter ranges, which parameters you include, the tolerance and number of maximum iterations, what Objective Function you evaluate performance with, and/or the Objective Function time window.
- Optimization is not automated calibration.
Resuming an Optimization Trial
Setting the Maximum Number of Iterations and Search Tolerance can be an iterative process. It might take a few tries to identify the maximum number of iterations and a search tolerance small enough to converge to a reasonable solution. With those larger models that take longer to run, starting out with a smaller maximum number of iterations and larger tolerance can save time. In two situations, the Simplex and Differential Evolution search methods can resume a search from a terminated state:
- If the search terminates without converging, because it has reached the maximum iteration limit
- If the search converges in fewer iterations than the maximum number of iterations
The user can continue a search that terminates by increasing the maximum number of iterations (for a search that has not converged) or decreasing the search tolerance (for a search that has converged). To resume the search, the user can only change either the maximum iteration (search has not converged) or the tolerance (search has converged) setting. If the user changes any other setting (parameters, Objective Function, etc.) the search state is no longer valid and the search will restart.