Download PDF
Download page Bed-load.
Bed-load
Bed-load Transport Equation
The bed-load transport equation may be written as
| 1) | \frac{\partial }{\partial t} \left(\frac{h C_{bk}}{\beta _{bk}}\right) +\nabla \cdot \left[ h (\boldsymbol{U} + \boldsymbol{U}_{bn} ) C_{bk} \right] = \nabla \cdot \left(\varepsilon_{bhk} h \nabla C_{bk} \right) + E_{bk} - D_{bk} |
where
C_{bk}: bed-load sediment concentration [M/L3]
β_{bk}: bed-load correction factors [-]
U: depth-averaged current velocity in jth - direction [L/T]
\boldsymbol{U}_{bn} : bed-load secondary flow correction velocity [L/T]
h: water depth [L]
ε_{bhk}: bed-load horizontal diffusion (mixing) coefficient [L2/T]
E_{bk} : bed-load erosion rate [M/L2/T]
D_{bk}: bed-load deposition rate [M/L2/T]
Bed-load Correction Factor
The bed-load correction factor is defined as the ration between the bed-load velocity and the depth-averaged current velocity
| 2) | \beta_{bk} = \frac{u_{bk}}{U} |
where
u_{bk}: bed-load velocity [L/T]
U : depth-averaged current velocity [L/T]
The bed-load correction factor may be specified as a constant or computed with one of several bed-load velocity formulas (presented in the following section).
Bed-load Velocity
The bed-load velocity is the average particle velocity during transport. It is not the average velocity of the bed-load material, which is what is typically measured in a tracer studies or mobile bed laboratory experiments. The bed-load velocity different formulations available are plotted in the figure below and described in the following sub sections. In general, the formulations produce similar results except for the Julien and Bounvilay (2013) formulation which does not have a critical threshold for bed-load transport.
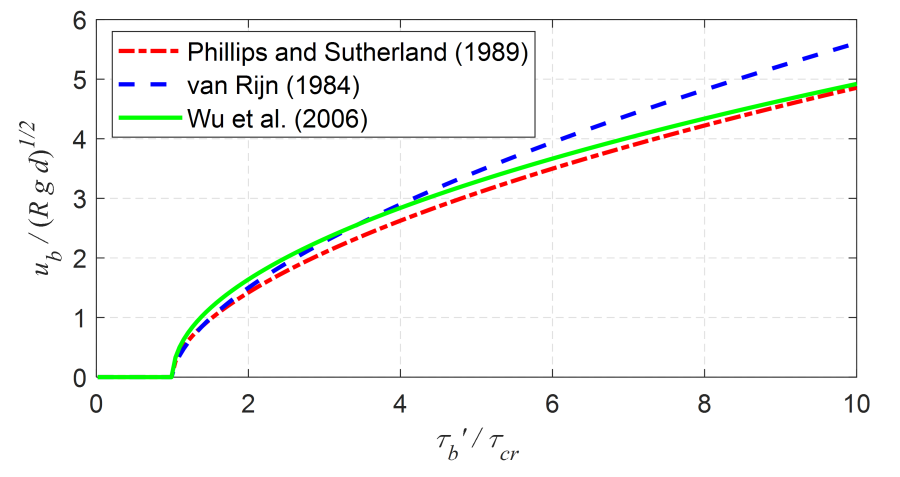
Figure 1. Comparison of bed-load velocity functions.
Phillips and Sutherland
Phillips and Sutherland (1989) proposed the following formula for the bed-load velocity
| 3) | u_{bk}=8.5\left\{\frac{\tau '_{b}}{\rho _{w}}\max \left[1-\left(\frac{\tau _{crk}}{\tau '_{b}}\right)^{1/2},0\right]\right\}^{1/2} |
where
τ'_b: grain-related bed shear stress [M/L/T2]
τ_{crk}: critical bed shear stress for the kth size class [M/L/T2]
ρ_{w}: water density [M/L3]
n': grain-related Manning’s roughness coefficient [T/L1/3]
van Rijn
The van Rijn (1984a) formula for computing the bed load velocity (ubk) is given by
| 4) | \frac{u_{bk}}{\sqrt{R_k g d_{k}}} = 1.5 \max \left(\frac{\tau'_b}{\tau _{crk}} - 1,0 \right)^{0.6} |
where
R_k: submerged specific gravity for the kth grain class [-]
\rho_{sk}: particle density for the kth grain class [M/L3]
\rho_{w}: water density [M/L3]
g: gravitational constant (~9.81 m/s2) [L/T2]
d_{k}: characteristic grain diameter for the kth size class [L]
τ'_b : grain-related bed shear stress [M/L/T2]
τ_{crk}: critical bed shear stress for the kth size class [M/L/T2]
The van Rijn (1984a) formula is based on laboratory experiments of Fernandez Luque (1974; 1976).
van Rijn-Wu
Wu et al. (2006) recalibrated the coefficients of the van Rijn (1984a) formula as
| 5) | \frac{u_{bk}}{\sqrt{R_k g d_k}} = 1.64\max \left(\frac{\tau^'_b}{\tau _{crk}}-1,0\right)^{0.5} |
where
R_k = \rho_{sk} / \rho_w − 1: submerged specific gravity for the kth grain class [-]
\rho_{sk}: particle density for the kth grain class [M/L3]
\rho_{w}: water density [M/L3]
g: gravitational constant (~9.81 m/s2) [L/T2]
d_{k}: characteristic grain diameter for the kth size class [L]
τ′_b: grain-related bed shear stress [M/L/T2]
τ_{crk}: critical bed shear stress for the kth size class [M/L/T2]
The Wu et al. (2006) formula produces similar bed-load velocities as the van Rijn (1984a) formula for low shear stresses but significantly lower bed-load velocities for high shear stresses where the van Rijn (1984a) departs from the other bed-load velocity formulations.
Bed-load Horizontal Diffusion Coefficient
The bed-load horizontal diffusion coefficient (εbk) represents the sediment mixing due to spatially and temporally varying bed-load velocities. The following formula is proposed for the bed-load horizontal diffusion coefficient.
| 6) | \varepsilon_{bk} = c_B u'_* d_k |
where
c_{B }: empirical coefficient (c_{B} \approx 5) [-]
u_{*}: bed shear velocity [L/T]
d_{k}: grain size diameter [L]
The bed-load horizontal mixing coefficient is much smaller than the suspended-load mixing coefficient. In addition, the dispersion produced by the mixing in the bed is usually much more significant than horizontal bed-load diffusion. Therefore, the bed-load diffusion coefficient can usually be ignored.