Download PDF
Download page Bed Roughness Predictors.
Bed Roughness Predictors
By default, the total bed roughness is set to the user-specified Manning's roughness coefficient utilized for hydrodynamics. The option is also available to compute the dynamically variable bed roughness based on one of three bed roughness predictors. These are formulations to compute bed roughness based on varying hydrodynamic and surface bed compositions. Here the following formulations are available:
- Limerinos (1970)
- Brownlie (1983)
- van Rijn (1984c)
- Karim (1995)
- Wu and Wang (1999)
A comparison of different bed roughness predictors is shown in the figure below. The Karim-van Rijn formulation utilizes the van Rijn (1984c) dune geometry formulas instead of Karim (1995). The Limerinos (1970) formula does not account for bedform roughness and is therefore constant with transport stage. The Wu and Wang (1999) and van Rijn (1984c) formulas produce similar results. The Wu and Wang (1999) formula produces bedform roughness even at transport stages less than one, while the formulations which utilize the van Rijn (1984c) dune geometry only produce bedform roughness for transport stages larger than one. The Brownlie (1983) formula has a sharp discontinuity between the lower and upper flow regimes. This discontinuity may cause stability problems in numerical models and so cautious must be practice when modeling such flows with the Brownlie formula.
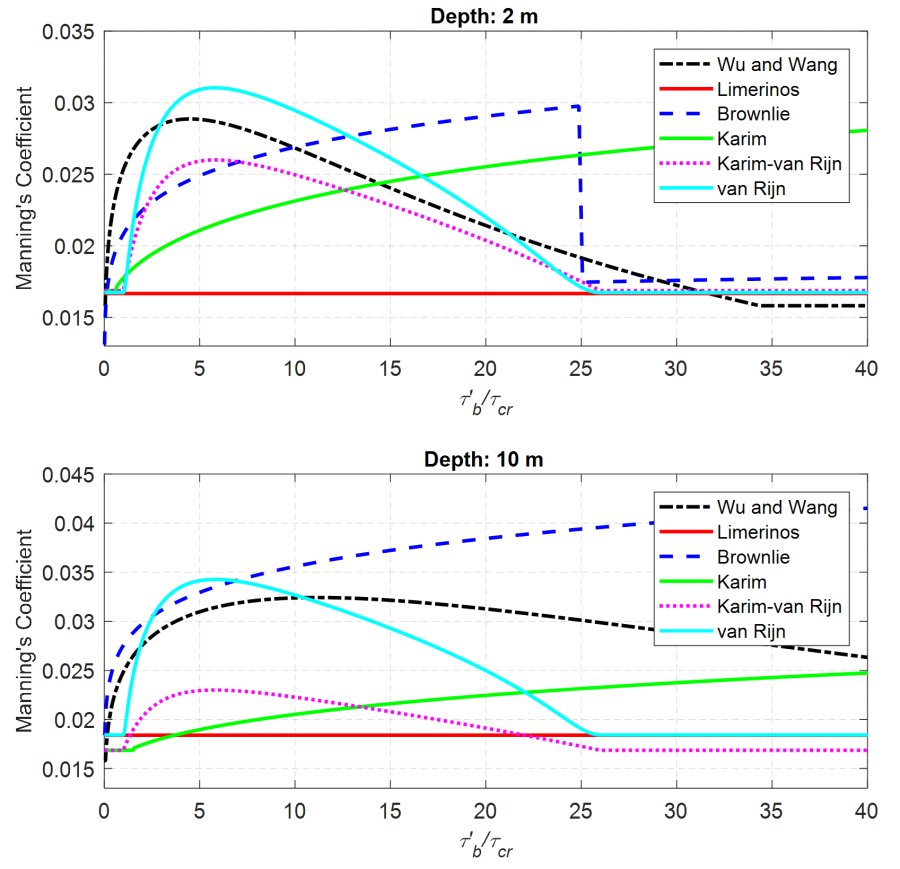
Figure 2 6. Comparison of different bed roughness predictors.
Limerinos
Limerinos (1956) developed a bed roughness predictor based on data from 11 gravel-bed streams in California as (see Figure below)
| 1) | n=\frac{0.0926AR^{1/6}}{1.16+2\log _{10}\left(R/d_{84}\right)} |
where
A=\left\{\begin{array}{ 1.219\,\,\,\,\mathrm{for}\,\mathrm{SI}\,\text{units}\\ 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{for}\,\text{English}\,\text{units} \end{array}\right.
n = Manning’s roughness coefficient [s/m1/3]
R = hydraulic radius [L]
d_{84} = 84th percentile diameter [L]
The equation is applicable to high in-bank flows in straight, gravel-bed channels. All the data used corresponded to Froude numbers less than 1. The Limerinos equation only accounts for the grain roughness in gravel-bed streams and does not include other contributions. Therefore, it may be used as the base value in the Cowan (1956) method. The above formula does not account for the full distribution of sediments and only consider a representative diameter. This is a limitation of the expressions when being applied to poorly sorted bed material.
Brownlie
Brownlie (1983) proposed separate resistance relationships for the lower and upper regimes as
| 2) | n=\left\{\begin{array} 1.6940\left(\frac{R}{d_{50}}\right)^{0.1374}S^{0.1112}\sigma _{g}^{0.1605}n'\,\,\,\,\,\mathrm{for}\,S>0.006\,\,\mathrm{or}\,F_{g}>1.25F'_{g}\colon \,\,\text{upper}\,\text{regime}\\ 1.0213\left(\frac{R}{d_{50}}\right)^{0.0662}S^{0.0395}\sigma _{g}^{0.1282}n'\,\,\,\,\,\mathrm{for}\,\,F_{g}<0.8F'_{g}\colon \,\,\text{lower}\,\text{regime} \end{array}\right. |
where
n = total manning’s roughness coefficient
q_{*}=\frac{Uh}{\sqrt{gd_{50}^{3}}} [ - ]
R = hydraulic radius associated with the bed [L]
S = slope [ - ]
d_{50} = median grain size [L]
σ_g = geometric standard deviation of bed material [ - ]
n = {0.041d_{50}}^{1/6} = Strickler grain roughness [s/m1/3]
F_{g} = \frac{U}{\sqrt{\rho gd_{50}(s-1)}} = grain Froude number [ - ]
F'_{g} = \frac{1.74}{S^{0.3333}} = slope parameter [ - ]
van Rijn
The van Rijn (1984c) alluvial roughness height predictor computed computes the total roughness ks as the sum of the grain and dune roughness:
| 3) | k_s = k_{s, g} + k_{s, d} |
where
ks = total roughness height [L]
k_{s,\,g} = grain roughness height [L]
k_{s, d} = dune roughness height [L]
The grain roughness is computed as
| 4) | k_{s, g} = 3d_{90} |
where d90 is the 90th percentile diameter. The dune roughness height is computed as (van Rijn 1984a)
| 5) | k_{s,d}=1.1\gamma _{d}\Delta _{d}\left[1-\exp \left(-25\frac{\Delta _{d}}{\lambda _{d}}\right)\right] |
where
γ_d = dune shape coefficient (~1.0) [ - ]
\Delta _{d} = dune height [L]
λ_d = dune length [L]
The dune shape coefficient, γd, is approximately 1.0 for dzunes with angle-of-repose faces as considered in van Rijn (1984). Dunes with more gently sloping faces have smaller shape coefficients as is common in the field. van Rijn (1993) proposed setting γd = 0.7 based on various field measurements of river systems. van Rijn (1984a) provided expressions for calculating the dune height and length and are shown in Equations (2-94) and (2-95). The figure below shows the dune roughness based on van Rijn (1984a) as a function of the sediment transport stage. Here the parameter is set to 1.0 for simplicity.
Karim
Karim (1995) developed a formula to predict bedform roughness for ripples, dunes and washed out dunes following a curve fit to flume and field measurements. The proposed formula for the total Manning’s roughness coefficient is as follows:
| 6) | n=0.037d_{50}^{0.126}\left(1.2+8.92\frac{\Delta }{h}\right)^{0.465} |
where
n = Manning’s roughness coefficient [s/m1/3]
d_{50} = median grain size diameter [m]
h = water depth [m]
\Delta = bedform height [m]
Karim (1995) proposed a formula for the bedform height. However, other formulas may also be used. In fact, it has been found that utilizing the van Rijn (1984c) formula for dune height produces results which are more consistent with the Wu and Wang (1999) formula which is described below.
Wu and Wang
Wu and Wang (1999) developed a formula to predict bedform roughness for ripples, dunes and washed out dunes following a curve fit to flume and field measurements. The proposed formula for the total Manning’s roughness coefficient is as follows:
| 7) | n = \max \left(\frac{d_{50}^{1/6}}{A_{n}},n_{g}\right) |
with
| 8) | \frac{A_{n}}{\sqrt{g}F_{r}^{1/3}}=\frac{8\left[1+0.0235\left(\tau '_{b}/\tau _{cr50}\right)^{1.25}\right]}{\left(\tau '_{b}/\tau _{cr50}\right)^{1/3}} |
where
n = Manning’s roughness coefficient [s/m1/3]
n_g = Grain-related Manning’s roughness coefficient [s/m1/3]
F_{r} = U/\sqrt{gh} = Froude number [ - ]
U = depth-averaged current velocity [L/T]
h = water depth [m]
g = gravity [L/T2]
τ′_b = grain shear stress [M/L/T2]
τ_{cr50} = critical shear stress corresponding to the median grain size [M/L/T2]
Wu and Wang (1999) computed the grain-related Manning’s roughness coefficient with the formula of Li and Liu (1963).