In order to close the system of equations describing the sediment transport, bed change, and bed sorting equations, the fractional depth-averaged total-load concentration potential (C_tk^*) must be estimated from an empirical formula. The depth-averaged concentration potential is defined as

1)	$\begin{array}{l}\displaystyle C_{tk}^{}=\frac{q_{tk}^{}}{Uh}\end{array}$

where q_tk^* is the total-load transport potential for the k^th sediment size class.

Ackers and White

The original Ackers and White (1973) was developed for to estimate the total load of uniform material. Ackers (1993) subsequently provided an update to the formula empirical coefficients. Day (1980) and Proffitt and Sutherland (1983) extended the original Ackers and White (1973) by multiplying it by a hiding and exposure correction factor. The fractional total-load transport potential is given by

2)	$\begin{array}{l}\displaystyle {q_{tk}}^* = ρ_wghU{X_{tk}}^*\end{array}$

where

$\begin{array}{l}{q_{tk}}^*\end{array}$ = sediment transport potential [M/L/T]

$\begin{array}{l}ρ_{w}\end{array}$ = water density [M/L³]

$\begin{array}{l}g\end{array}$ = gravity acceleration [L/T²]

$\begin{array}{l}h\end{array}$ = water depth [L]

$\begin{array}{l}U\end{array}$ = depth-averaged current velocity [L/T]

$\begin{array}{l}{X_{tk}}^*\end{array}$ = sediment concentration potential by weight

The sediment concentration potential is determined from

3)	$\begin{array}{l}\displaystyle \frac{X_{tk}^{}h\rho _{w}}{d_{k}\rho _{sk}}\left(\frac{u_{}}{U}\right)^{n}=\Lambda \left(\frac{F_{grk}}{A_{c}}-1\right)^{m}\end{array}$

where

$\begin{array}{l}F_{grk}\end{array}$ = sediment mobility factor [-]

$\begin{array}{l}u_{*}=\sqrt{\tau _{b}/\rho _{w}}\end{array}$ = bed shear velocity [M/T]

$\begin{array}{l}ρ_{sk}\end{array}$ = sediment density [M/L³]

$\begin{array}{l}\Lambda\end{array}$ = $\begin{array}{l}\Lambda (d_{*k})\end{array}$ = empirical coefficient [-]

$\begin{array}{l}A_{c}\end{array}$ = $\begin{array}{l}A_c(d_{*k})\end{array}$ = empirical coefficient [-]

$\begin{array}{l}n\end{array}$ = $\begin{array}{l}n(d_{* k})\end{array}$ = empirical exponent [-]

$\begin{array}{l}m\end{array}$ = $\begin{array}{l}m(d_{* k})\end{array}$ = empirical exponent [-]

The sediment mobility factor is given by

4)	$\begin{array}{l}\displaystyle F_{grk}=\eta _{k}\frac{u_{*}^{n}}{\sqrt{R_{k}gd_{k}}}\left[\frac{U}{\sqrt{32}\log _{10}(10h/d_{k})}\right]^{1-n}\end{array}$

where

$\begin{array}{l}ρ_{sk}\end{array}$ = sediment density [M/L³]

$\begin{array}{l}ρ_{w}\end{array}$ = water density [M/L³]

$\begin{array}{l}η_{k}\end{array}$ = hiding and exposure correction factor [-]

$\begin{array}{l}τ_{b}\end{array}$ = bed shear stress [M/L/T²]

$\begin{array}{l}d_{k}\end{array}$ = sediment diameter [L]

The firs term in the above equation corresponds to the bed-load transport while the second the suspended-load transport. The formula is based on the understanding that bed load is attributed to the grain shear stress while the suspended load is related to the turbulence intensity. The empirical coefficients were revised by Ackers (1993) as

5)

$\begin{array}{l}n=\begin{cases} 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{for}\,\,d_{*k}\leq 1\\ 1-0.56\log _{10}(d_{*k})\,\,\mathrm{for}\,\,1< d_{*k}\leq 60\\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{for}\,\,d_{*k}>60 \end{cases}\right.\end{array}$

6)	$\begin{array}{l}A_{c}=\begin{cases} 0.23d_{k}^{-1/2}+0.14\,\,\,\,\mathrm{for}\,\,d_{k}\leq 60\\ 0.17\,\,\text{otherwise} \end{cases}\right.\end{array}$

7)	$\begin{array}{l}m=\begin{cases} 6.83d_{k}^{-1}+1.67\,\,\,\,\mathrm{for}\,d_{k}\leq 60\\ 1.78\,\,\text{otherwise} \end{cases}\right.\end{array}$

8)	$\begin{array}{l}\Lambda =\left\{\begin{array} \exp \left\{2.791\log _{10}(d_{k})-0.98\left[\log _{10}(d_{k})\right]^{2}-3.46\right\}\,\,\,\,\,\mathrm{for}\,\,d_{*k}\leq 60\\ 0.0025\,\,\,\,\text{otherwise} \end{array}\right.\end{array}$

Wu (2007) tested and compared the Ackers-White (AW) formula for graded sediments and found that it tends to over predict the transport significantly for fine sediments less than 0.2 mm. However, the Ackers-White formula performs very well for uniform sediments. Day (1980) and Proffitt and Sutherland (1983) developed hiding and exposure correction factors for the Ackers-White formula and are available here to the user. It is noted that in AW, hiding and exposure is considered through a transport multiplication factor rather than through the sediment mobility.

Engelund-Hansen

The Engelund-Hansen (1967) formula is a total-load transport potential formula based on stream power. The formula is most appropriate for environments with uniform sediments and dominated by suspended load. The formula has been modified here for multiple grain classes and to include a critical shear stress for sediment transport as

9)

$\begin{array}{l}q_{tk}^{*}=\begin{cases} 0.05\eta _{k}\rho _{sk}U^{2}\sqrt{\frac{d_{k}}{gR_{k}}}\left(\frac{\tau _{b}}{g\left(\rho _{sk}-\rho _{w}\right)d_{k}}\right)^{3/2}\,\,\,\mathrm{for}\,\,\tau _{b}>\tau _{crk}\\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{otherwise} \end{cases}\right.\end{array}$

where

$\begin{array}{l}{q_{tk}}^*\end{array}$ = sediment transport capacity [M/L/T]

$\begin{array}{l}τ_{b}\end{array}$ = bed shear stress [M/L/T²]

$\begin{array}{l}τ_{crk}\end{array}$ = critical shear stress [M/L/T²]

$\begin{array}{l}U\end{array}$ = current velocity magnitude [L/T]

$\begin{array}{l}R_{k}\end{array}$ = $\begin{array}{l}ρ_{sk}/ρ_w− 1\end{array}$ = submerged specific gravity of a particle [-]

$\begin{array}{l}ρ_{sk}\end{array}$ = sediment density [M/L³]

$\begin{array}{l}ρ_{w}\end{array}$ = water density [M/L³]

$\begin{array}{l}d_{k}\end{array}$ = grain class diameter [L]

The suggested applicability of the Engelund-Hansen formula is for $\sqrt{d_{75}/d_{25}}$<1.6 and d₅₀<0.15 mm. It is noted that the Engelund-Hansen formula does not include a critical threshold for transport. England Hansen is the simplest transport equations. Application should be restricted to sand systems.

Laursen-Copeland

Laursen (1968) developed a total-load sediment transport formula based on flume experiments initially and later expanded it to included data from Arkansas River. Copeland and Thomas. (1989) then generalized the equation for gravel transport. One important aspect of the Laursen-Copeland formula is that it is valid from silts to gravel.

10)	$\begin{array}{l}\displaystyle q_{tk}^{}=a\rho _{w}Uh\left(\frac{d_{k}}{h}\right)^{7/6}\left(\frac{\theta '_{b}}{\theta _{crk}}-1\right)^{n}f_{tk}^{LC}\left(\frac{u'_{}}{\omega _{sk}}\right)\end{array}$

where

$\begin{array}{l}{q_{tk}}^*\end{array}$ = sediment transport capacity [M//L/T]

$\begin{array}{l}a\end{array}$ = 0.01

$\begin{array}{l}θ'_{b}\end{array}$ = grain-related Shields number [-]

$\begin{array}{l}θ_{crk}\end{array}$ = critical Shields number [-]

$\begin{array}{l}U\end{array}$ = current velocity magnitude [L/T]

$\begin{array}{l}h\end{array}$ = water depth [L]

$\begin{array}{l}n\end{array}$ = empirical coefficient (default is 1.0) [-]

$\begin{array}{l}ρ_{w}\end{array}$ = water density [M/L³]

$\begin{array}{l}ω_{sk}\end{array}$ = sediment particle fall velocity [L/T]

$\begin{array}{l}d_{k}\end{array}$ = grain class diameter [L]

The transport function f_tk^LC(u_*/ω_sk) is approximated by the following regression equation:

11)

$\begin{array}{l}f_{tk}^{LC}\left(\frac{u_{*}}{\omega _{sk}}\right)=\begin{cases} 7.04\times 10^{15}\left(\frac{u_{*}}{\omega _{sk}}\right)^{22.99}\,\,\mathrm{for}\,\,\frac{u_{*}}{\omega _{sk}}\leq 0.225\\ 40\frac{u_{*}}{\omega _{sk}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{for}\,\,0.225< \frac{u_{*}}{\omega _{sk}}\leq 1.0\\ 40\left(\frac{u_{*}}{\omega _{sk}}\right)^{1.843}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{for}\,\,1.0< \frac{u_{*}}{\omega _{sk}} \end{cases}\right.\end{array}$

Larson (1968) and Copeland (1989) used a critical Shields number of 0.039. In HEC-RAS 2D sediment the Shields number may be calculated with another method or be user-specified. In addition the coefficient a and exponent n may be modified by the user. However, it is recommended to calibrate the transport formulas using the transport scaling and mobility factors.

Meyer-Peter and Müller

The Meyer-Peter and Müller (MPM) formula (1948) is a bed-load formula developed from flume experiments of sand and gravel under plane bed conditions. It was originally developed for uniform sediment beds. HEC-RAS uses the version of MPM from Vanoni (1975), ASCE Manual 54, the version used in HEC 6. This version includes a form drag correction (the RKR parameter, based on the roughness element ratio, (k_b/k_r)^3/2, computed from the DarcyWeisbach bed fiction factor). The form drag correction isolates grain shear, computing transport based on the bed shear component acting only on the particles. The form drag correction should be unnecessary in plane-bed conditions, so some versions of MPM exclude it. Wong and Parker (2006) demonstrate that using MPM without the form drag correction over-predicts bed load transport.

12)	$\begin{array}{l}\displaystyle \frac{q_{bk}^{*}}{\sqrt{R_{k}gd_{k}^{3}}}=A_{M}\rho _{sk}\left(\theta '_{b}-\theta _{crk}\right)^{{E_{M}}}\end{array}$

where

$\begin{array}{l}\theta '_{b}=\frac{\tau '_{b}}{(\rho _{sk}-\rho _{w})gd_{k}}\end{array}$ = grain-related Shields parameter [-]

$\begin{array}{l}ρ_{sk}\end{array}$ = sediment density [M/L³]

$\begin{array}{l}ρ_{w}\end{array}$ = water density [M/L³]

$\begin{array}{l}θ_{crk}\end{array}$ = critical Shields parameter [-]

$\begin{array}{l}A_{M}\end{array}$ = empirical coefficient [-]

Meyer-Peter Müller (1948) estimated A_M = 8, E_M = 3/2, and θ_crk = 0.047. However, Wong and Parker (2006) recalibrated the equation and found A_M = 3.97, E_M = 1.6, and θ_crk=0.0495. The MPM formula is most applicable to uniform gravel bed and tends to under-predict transport for fine sands and silts.

Soulsby-van Rijn

Soulsby (1997) proposed the following equation for the total load sediment transport rate

13)	$\begin{array}{l}q_{bk}^{*}=\begin{cases} 0.005Uh\left(\frac{U-U_{crk}}{\sqrt{R_{k}gd_{k}}}\right)^{2.4}\left(\frac{d_{k}}{h}\right)^{1.2}\,\,\,\,\,\mathrm{for}\,\,U>U_{crk}\,\,\\ 0\,\,\,\,\,\,\,\text{otherwise}\,\, \end{cases}\right.\end{array}$

14)	$\begin{array}{l}q_{sk}^{}=\begin{cases} 0.012Uh\left(\frac{U-U_{crk}}{\sqrt{R_{k}gd_{k}}}\right)^{2.4}\left(\frac{d_{k}}{h}\right)d_{k}^{-0.6}\,\,\,\,\mathrm{for}\,\,U>U_{crk}\\ 0\,\,\,\,\,\,\text{otherwise}\,\, \end{cases}\right.\end{array}$

where

$\begin{array}{l}{q_{bk}}^*\end{array}$ = fractional bed-load sediment transport potential [L²/T]

$\begin{array}{l}{q_{sk}}^*\end{array}$ = fractional suspended-load sediment transport potential [L²/T]

$\begin{array}{l}R_{k}\end{array}$ = ρ_sk/ρ_w − 1 = submerged specific gravity of a particle [-]

$\begin{array}{l}ρ_{sk}\end{array}$ = sediment density [M/L³]

$\begin{array}{l}ρ_{w}\end{array}$ = water density [M/L³]

$\begin{array}{l}U\end{array}$ = effective depth-averaged current velocity [m/s]

$\begin{array}{l}U_{crk}\end{array}$ = critical depth-averaged velocity for incipient motion [m/s]

The Soulsby-van Rijn formula was developed by calibrating the above equations to the van Rijn (1993) sediment transport model. The formulas were originally proposed for well-sorted sediments. The formulas have been modified here for nonuniform sediments by replacing the median grain size with the grain class diameter and multiplying the critical depth-averaged current velocity with a hiding and exposure correction factor. Here the Wu et al. (2000) hiding and exposure correction factor is utilized but in principle others may also be used. van Rijn (1984a,b; 2007a,b) computed the critical depth-averaged current velocity using the van Rijn formula.

Toffaleti

Toffaleti (1968) developed a total-load transport formula primarily for sand particles. The method splits the water column into three vertical zones as shown in the figure below.

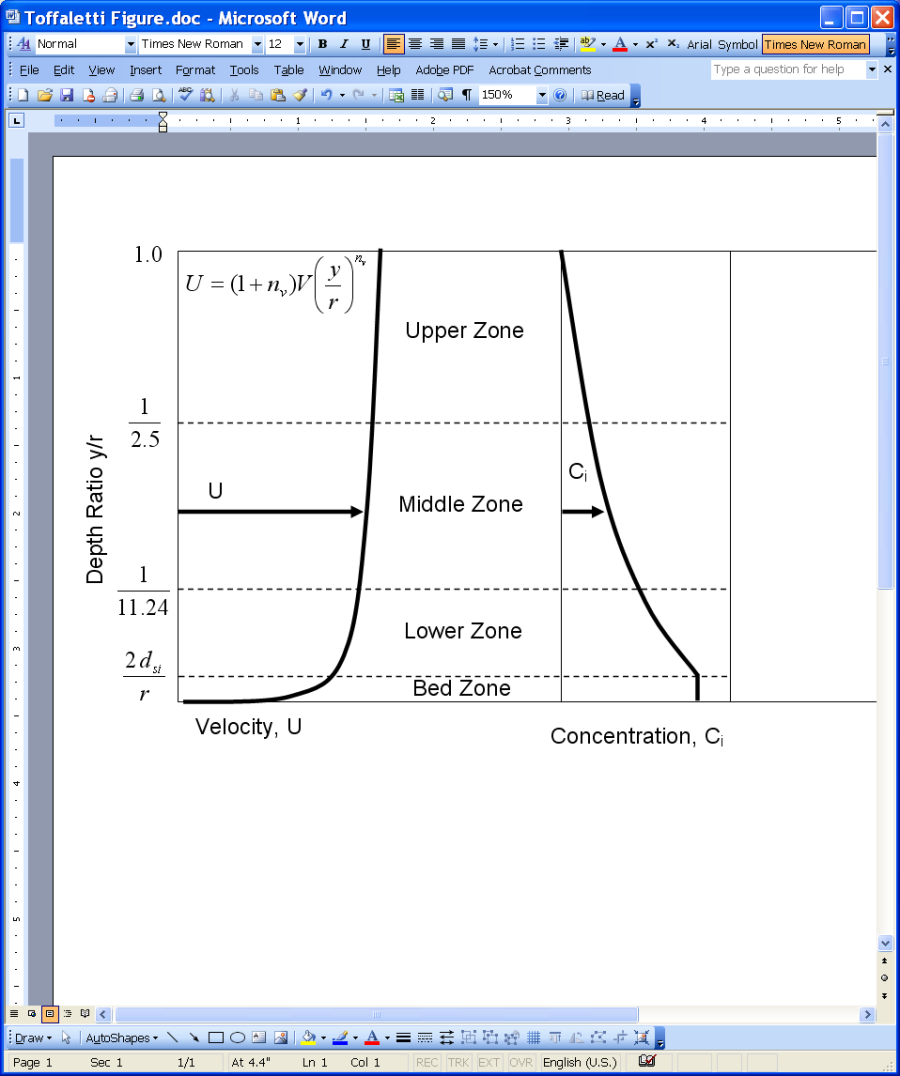
Figure 2 20. Toffaleti total-load transport zones.

The formula computes the concentration in each of the three zones using a Rouse concentration profile. The suspended-load transport potential for each zone is computed analytically assuming a current velocity profile. The total-load transport potential is computed as the sum of the three suspended-load zones and the bed-load zone. The sediment transport potential formulas are not based on excess shear but rather are regression equations based on sediment and water properties, and hydraulic variables. The Toffalti formula was originally developed for bulk transport but here it is applied to individual grain classes. The Toffaleti formula is usually applied at "large" rivers since most of the data used to develop it were from large suspended-load dominant rivers. The Toffaleti bed-load transport potential does not perform for gravel size or coarse particles. For this reason, the option is available to replace the bed-load transport potential in the Toffaleti formula with an estimate from the Meyer-Peter and Muller formula. This formula is referred to as the Toffaleti-MPM formula.

Van Rijn

The van Rijn sediment transport formula are given by (1984a,b; 2007a,b)

15)	$\begin{array}{l}\displaystyle q_{bk}^{*}=0.015Uh\left(\frac{U-U_{crk}}{\sqrt{R_{k}gd_{k}}}\right)^{1.5}\left(\frac{d_{k}}{h}\right)^{1.2}\end{array}$

16)	$\begin{array}{l}\displaystyle q_{sk}^{}=0.012Uh\left(\frac{U-U_{crk}}{\sqrt{R_{k}gd_{k}}}\right)^{2.4}\left(\frac{d_{k}}{h}\right)d_{k}^{-0.6}\end{array}$

where

$\begin{array}{l}{q_{bk}}^*\end{array}$ = fractional bed-load sediment transport potential [L²/T]

$\begin{array}{l}{q_{sk}}^*\end{array}$ = fractional suspended-load sediment transport potential [L²/T]

$\begin{array}{l}R_{k}\end{array}$ = $\begin{array}{l}ρ_{sk}/ρ_w−1\end{array}$ = submerged specific gravity of a particle [-]

$\begin{array}{l}ρ_{sk}\end{array}$ = sediment density [M/L³]

$\begin{array}{l}ρ_{w}\end{array}$ = water density [M/L³]

$\begin{array}{l}U\end{array}$ = effective depth-averaged current velocity [m/s]

$\begin{array}{l}U_{crk}\end{array}$ = critical depth-averaged velocity for incipient motion [m/s]

The van Rijn formulas were originally proposed for well-sorted sediments. The formulas have been modified here for nonuniform sediments by replacing the median grain size with the grain class diameter and multiplying the critical depth-averaged current velocity with a hiding and exposure correction factor.

Wilcock and Crowe

Wilcock (2001) and Wilcock and Crowe (2003) developed a surface-based bed-load transport equation for graded beds with sand and gravel. The transport potential of the Wilcock and Crowe (WC) formula is given by

17)	$\begin{array}{l}\displaystyle q_{bk}^{}=\frac{u_{}^{3}W_{k}^{*}}{R_{k}g}\end{array}$

where

$\begin{array}{l}{q_{bk}}^*\end{array}$ = fractional bed-load sediment transport potential [L²/T]

$\begin{array}{l}u_{*}\end{array}$ = bed shear velocity [L/T]

$\begin{array}{l}{W_{k}}*\end{array}$ = transport function [-]

$\begin{array}{l}R_{k}\end{array}$ = $\begin{array}{l}ρ_{sk}/ρ_w−1\end{array}$ = submerged specific gravity of grain class [-]

$\begin{array}{l}ρ_{sk}\end{array}$ = sediment grain density [M/L³]

$\begin{array}{l}ρ_{w}\end{array}$ = water density [M/L³]

$\begin{array}{l}g\end{array}$ = gravitational constant [L/T^2]

The transport function is given by

18)	$\begin{array}{l}W_{k}^{*}=\begin{cases} 0.002\phi ^{7.5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{for}\,\,\phi < 1.35\\ 14\left(1-\frac{0.894}{\phi ^{0.5}}\right)^{4.5}\,\,\,\mathrm{for}\,\,\phi \geq 1.35 \end{cases}\right.\end{array}$

where

$\begin{array}{l}ϕ\end{array}$ = $\begin{array}{l}τ_b/τ_{r, k}\end{array}$ = sediment mobility [-]

$\begin{array}{l}τ_{b}\end{array}$ = bed shear stress [-]

$\begin{array}{l}τ_{r, k}\end{array}$ = reference shear stress

Wu et al.

The bed- and suspended-load transport formula of Wu et al. (2000) are given by

19)	$\begin{array}{l}q_{bk}^{*}=\begin{cases} 0.0053\sqrt{R_{k}gd_{k}^{3}}\left(\frac{\tau '_{b}}{\tau _{crk}}-1\right)^{2.2}\,\,\mathrm{for}\,\,\tau '_{b}>\tau _{ck}\\ 0\,\,\,\,\,\text{otherwise} \end{cases}\right.\,\,\,\end{array}$

20)

$\begin{array}{l}q_{sk}^{*}=\begin{cases} 2.62\times 10^{-5}\sqrt{R_{k}gd_{k}^{3}}\left[\left(\frac{\tau _{b}}{\tau _{crk}}-1\right)\frac{U}{\omega _{sk}}\right]^{1.74}\,\,\,\,\mathrm{for}\,\,\tau _{b}>\tau _{ck}\,\mathrm{and}\,\,\tau '_{b}>\tau _{ck}\,\,\,\\ 0\,\,\,\,\,\text{otherwise} \end{cases}\right.\end{array}$

where

$\begin{array}{l}{q_{bk}}^*\end{array}$ = fractional bed-load sediment transport potential [L²/T]

$\begin{array}{l}{q_{sk}}^*\end{array}$ = fractional suspended-load sediment transport potential [L²/T]

$\begin{array}{l}R_{k}\end{array}$ = $\begin{array}{l}ρ_{sk}/ρ_w−1\end{array}$ = submerged specific gravity of a particle [-]

$\begin{array}{l}ρ_{sk}\end{array}$ = sediment density [M/L³]

$\begin{array}{l}ρ_{w}\end{array}$ = water density [M/L³]

$\begin{array}{l}τ_{b}\end{array}$ = bed shear stress [M/L/T²]

$\begin{array}{l}τ'_{b}\end{array}$ = skin bed shear stress [M/L/T²]

$\begin{array}{l}τ_{crk}\end{array}$ = critical shear stress [M/L/T²]

$\begin{array}{l}d_{k}\end{array}$ = Sediment diameter [L]

Since the total bed shear stress is equal or larger than the skin bed shear stress, it is possible for the original formulation to produce suspended load without bed load. This situation is considered unrealistic and is avoided here by adding the additional condition in the above equation.

Yang

Yang (1979; 1984) developed a total sediment transport method based on the regression of potential energy dissipation per unit weight of water and the total sediment concentration:

21)

$\begin{array}{l}\log _{10}\left(C_{tk}^{*}\right)=\begin{cases} M+N\log _{10}\left[\frac{S_{f}}{\omega _{sk}}\left(U-U_{crk}\right)\right]\,\,\,\,\mathrm{for}\,\,U>U_{crk}\,\,\\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{otherwise} \end{cases}\right.\end{array}$

22)

$\begin{array}{l}M=\begin{cases} 5.435-0.286\log _{10}\left(\frac{\omega _{sk}d_{k}}{\nu }\right)-0.457\log _{10}\left(\frac{u_{*}}{\omega _{sk}}\right)\,\,\,\mathrm{for}\,\,d_{k}< 2\,\mathrm{mm}\\ 6.681-0.681\log _{10}\left(\frac{\omega _{sk}d_{k}}{\nu }\right)-4.816\log _{10}\left(\frac{u_{*}}{\omega _{sk}}\right)\,\,\,\mathrm{for}\,\,2\,\mathrm{mm}< d_{k}< 10\,\mathrm{mm} \end{cases}\right.\end{array}$

23)

$\begin{array}{l}N=\begin{cases} 1.799-0.409\log _{10}\left(\frac{\omega _{sk}d_{k}}{\nu }\right)-0.314\log _{10}\left(\frac{u_{*}}{\omega _{sk}}\right)\,\,\,\,\mathrm{for}\,\,d_{k}< 2\,\mathrm{mm}\\ 2.784-0.305\log _{10}\left(\frac{\omega _{k}d_{k}}{\nu }\right)-0.282\log _{10}\left(\frac{u_{*}}{\omega _{sk}}\right)\,\,\,\,\mathrm{for}\,\,2\,\mathrm{mm}< d_{k}< 10\,\mathrm{mm} \end{cases}\right.\end{array}$

where

$\begin{array}{l}{C_{tk}}^*\end{array}$ = sediment concentration in parts per million (ppm) by weight

$\begin{array}{l}u_{*}\end{array}$ = bed shear velocity [L/T]

$\begin{array}{l}ω_{sk}\end{array}$ = sediment fall velocity [L/T]

$\begin{array}{l}ν\end{array}$ = kinematic water viscosity [L²/T]

$\begin{array}{l}U\end{array}$ = depth-averaged current velocity [L/T]

$\begin{array}{l}U_{crk}\end{array}$ = critical depth-averaged current velocity [L/T]

$\begin{array}{l}S_{f}\end{array}$ = friction slope [-]

The Yang (1973) transport equations tend to overestimate transport for very coarse sands and there is also a sharp discontinuity between sand and gravel at d_s = 2 mm.

Download PDF

Transport Potential Formulas

Ackers and White

Engelund-Hansen

Laursen-Copeland

Meyer-Peter and Müller

Soulsby-van Rijn

Toffaleti

Van Rijn

Wilcock and Crowe

Wu et al.

Yang