Download PDF
Download page Critical Thresholds for Transport and Erosion.
Critical Thresholds for Transport and Erosion
Noncohesive Sediments
The critical and reference shear stresses are related to the critical and reference Shields numbers by
| 1) | \frac{\tau _{cr}}{(\rho _{s}-\rho _{w})gd}=\theta _{cr} |
| 2) | \frac{\tau _{r}}{(\rho _{s}-\rho _{w})gd}=\theta _{r} |
where
τ_{cr} = critical shear stress for noncohesives [M/L/T2]
τ_r = reference shear stress for noncohesives [M/L/T2]
θ_{cr} = critical Shields parameter for noncohesives [-]
θ_r = reference Shields parameter for noncohesives [-]
ρ_s = sediment grain density [M/L3]
ρ_w = water density [M/L3]
g = gravitational constant [L/T2]
d = grain diameter [L]
The formula for computing the critical Shields or reference Shields number is automatically selected by the program depending on the transport potential formula selected. However, the formula may be overwritten. Some of the transport formula utilize constant Shields parameters while others utilize a Shields parameter as function of the non-dimensional grain diameter.
Below is a comparison of the three methods to compute the Shields parameter which are not constant.
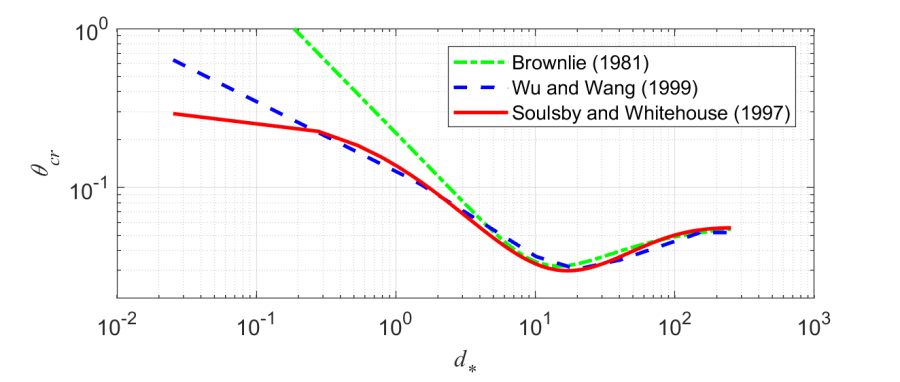
Figure 2-21. Example Shields parameter formulations.
Soulsby and Whitehouse
Soulsby and Whitehouse (1997) proposed the following formula for the critical Shields Parameter
| 3) | \theta _{cr}=\frac{0.3}{1+1.2d_{*}}+0.055\left[1-\exp \left(-0.02d_{*}\right)\right] |
Laursen and Laursen-Copeland
The Laursen (1968) and Laursen and Copeland (Copeland 1989) transport potential formula utilize the following critical Shields number for incipient motion
| 4) | θ_{cr} = 0.039 |
This equation should only be used in combination with Laursen and Copeland transport potential formula.
Meyer-Peter and Muller
Meyer-Peter and Müller (1948) utilized a constant Shields number of
| 5) | θ_cr = 0.047 |
This equation should only be used in combination with the Meyer-Peter and Muller transport potential formula.
Wilcock and Crowe
In the Wilcock transport potential formula, a reference Shields number is computed for the substrate which is a function of the sand content of the bed surface
| 6) | θ_r = 0.021 + 0.015 \exp(−2000 f_S) |
where θr is the reference Shields number for the noncohesive sediment mixture and fS is the fraction of sand on the surface.
Wu et al.
The sediment transport equations of Wu et al. (2000) utilize a simple approximation of the critical Shields number as a constant value.
| 7) | θ_{cr} = 0.03 |
This equation is used in combination with the bed load and total load equations from Wu et al. (2000).
van Rijn
The critical depth-averaged velocity (Ucr) is calculated using the formula proposed by van Rijn (1984c)
| 8) | U_{cr}=\left\{\begin{array}{l} 0.19d_{50}^{0.1}\log _{10}\left(\frac{4h}{d_{90}}\right)\mathrm{for}0.1\leq d_{50}\leq 0.5\,\mathrm{mm}\\ 8.5d_{50}^{0.6}\log _{10}\left(\frac{4h}{d_{90}}\right)\,\,\,\,\,\,\,\mathrm{for}\,\,0.5\leq d_{50}\leq 2.0\,\mathrm{mm} \end{array}\right. |
where d50 and d90 are the sediment grain size in meters of 50th and 90th percentiles, respectively. The above criteria are used in the van Rijn (2007a,b) and Soulsby-van Rijn (Soulsby 1997) transport formulas. For use in the multiple-sized sediment transport model, the particle diameters d50 and d90 are replaced with dk for simplicity.
Yang
Yang (1973) proposed the following formula for the critical depth-averaged velocity:
| 9) | \frac{U_{cr}}{\omega _{sd}}=\left\{\begin{array} \frac{2.5}{\log _{10}\left(\frac{u_{*}d}{\nu }\right)-0.06}+0.66\,\,\,\,\,\mathrm{for}\,\,1.2<\frac{u_{*}d}{\nu }<70\\ 2.05\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{for}\,\,\frac{u_{*}d}{\nu }\geq 70 \end{array}\right. |
where
u_* = bed shear velocity [L/T]
ω_{sd} = particle free settling velocity [L/T]
d = particle diameter [L]
ν = water kinematic viscosity [L2/T]
The Yang (1973) formula is the default formula utilized with the Yang (1973) transport potential formula.
Cohesive Sediments
For cohesive sediments, the critical shear stress for erosion is significantly affected by consolidation (i.e. varying dry bulk density). Several authors have proposed formulations for the critical shear stress as a function of the dry bulk density. Here the formulation by Owen (1975) is utilized because of its simplicity and the reduced number of input parameters required. In Owen’s formulation the critical shear stress for erosion is computed as a function of the dry bulk density as
| 10) | τ_{ce} = a{ρ_d}^b |
where
τ_{ce} = critical shear stress [M/L/T2]
ρ_d = dry bulk density [M/L3]
a = empirical coefficient
b = empirical coefficient
Generally, the value of a decreases as b increases. When a single bed layer is specified the coefficient, b is set to one and a is estimated from the initial erosion critical shear. If more than one bed layer is specified, than the empirical coefficients are estimated with a weighted least-squared method with the weight being the inverse of the dry bulk densities.
Owen (1975) reported of a = 6.85×10 − 6 and b = 2.44. Zheng and An (2017) present different values of a and b as a function of the solid content by weight of silts and clays. Liu et al. (2002) reported calibration fits of a = 6.30×10 − 4, b = 1.44, and a = 5.77×10 − 5, b = 1.41, at two stations in the Tanshui River, Taiwan. Perera and Wu (2016) compiled a large set of measurements from various sources and fit the coefficients a = 7.46×10 − 7, b = 2.27.
In addition to the critical shear stress for erosion, the power-law formula is used to fit all of the other cohesive parameters; namely the critical shear stress for mass wasting, τcM, the erosion rate coefficient, M, and, mass wasting coefficient, Mw.
Mixed Cohesive/Noncohesive Sediments
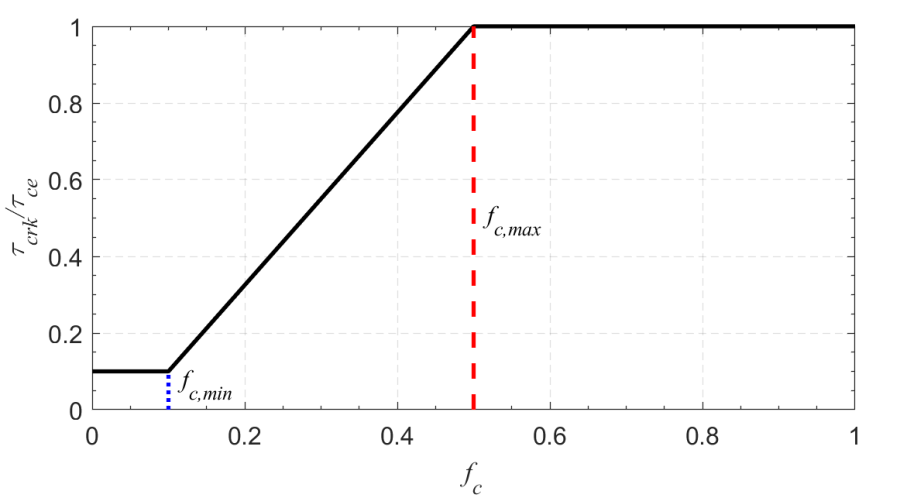
Figure 2 22. Example Shields parameter formulations.
In the case that the transport formula utilizes a critical Shields parameter or critical current velocity, the above formulation may still be applied by converting the critical Shields or critical current velocity into a critical shear stress, applying the above formulation, and then converting back to a critical Shields parameter or critical current velocity.