Aggressive Erosion or Deposition at the Model Boundary
1. Capacity/Load/Gradation Mismatch
Major deposition and erosion at the model boundary can be a mismatch between the capacity and the load and/or the gradation of the boundary condition. This is comparable to the 1D trouble shooting approach described here.
2. Misplaced Equilibrium Boundary Condition
An equilibrium load boundary condition sets the load to the boundary hydraulics and bed material, but can still deposit or erode if the upstream "cross section" and gradation do not reflect transport along the rest of the reach.
It is also important to select your boundary condition carefully with respect to structures. Place the boundary condition in a location that reflects the actual conveyance zone, or the boundary condition will spread flow and sediment across the whole numerical river.

3. Tail Water Control
The equilibrium boundary condition pictured below deposited aggressively along the upstream reach (blue). Upon closer inspection the deposition was just reworked erosion at the model boundary. The model scoured >70ft at the upstream boundary condition in response to a high velocity jet at the model boundary.

The energy grade slope was too high which brought flow into the model in a high-gradient jet. The Tail Water check in the upstream flow boundary condition can fix that. It looks to see if tailwater effects reduce the boundary slope. The TW Check should be selected in most cases.

Floodplain Roughness is Too High
Hydraulic models are not very sensitive to floodplain roughness. Manning's n values between 0.06 and 0.2 (or even higher are common). But sediment transport is very sensitive to bed roughness, and the trend can be counterintuitive. Shear stress is a function of the friction slope, which - by Manning's equation - is proportional to the square of the roughness parameter.
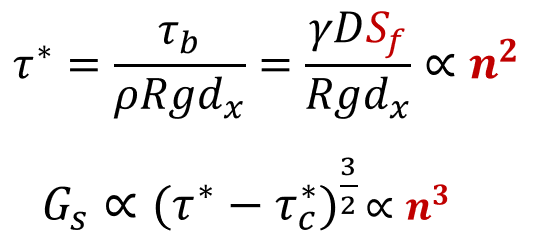
Then, transport often raises the shear to the 1.5 power, making it proportional to the n-value cubed.
Therefore, transport not only increases with higher n values (all else constant) the increase is highly non-linear. The difference in water surfaces between a floodplain n-value of 0.06 and 0.12 can be very small because most of the conveyance is in the channel. But transport increases by a factor of 8 (2X^3) despite a lower velocity. It can also increase transport in the channel because it decreases floodplain conveyance, increasing channel flow.
Therefore, it is very important to estimate appropriate Manning's roughness for the floodplain, which is often lower than estimated for hydraulic models.