Download PDF
Download page Shallow Water or Diffusion Wave Equations.
Shallow Water or Diffusion Wave Equations
As mentioned previously, HEC-RAS has the ability to perform two-dimensional unsteady flow routing with either the Shallow Water Equations (SWE) or the Diffusion Wave equations (DWE). HEC-RAS has three equation sets that can be used to solve for the flow moving over the computational mesh, the Diffusion Wave equations; the original Shallow Water equations (SWE-ELM, which stands for Shallow Water Equations, Eulerian-Lagrangian Method); and a new Shallow Water equations solution that is more momentum conservative (SWE-EM, which stands for Shallow Water Equations, Eulerian Method). The SWE also have options for modeling turbulence and Coriolis effects. See Chapter 2 of the Hydraulic reference manual for the theory on the development of these equations for use in HEC-RAS.
Within HEC-RAS the Diffusion Wave equations are set as the default, however, the user should always test if the Shallow Water equations are need for their specific application. A general approach is to use the Diffusion wave equations while developing the model and getting all the problems worked out (unless it is already known that the Full Saint Venant equations are required for the data set being modeled). Once the model is in good working order, then make a second HEC-RAS Plan and switch the equation set to the SWE option (SWE will generally require a smaller computation interval than the Diffusion wave method to run in a stable manner). Run this second plan and compare the two answers throughout the system. If there are significant differences between the two runs, the user should assume the SWE (Saint Venant equations) answer is more accurate, and proceed with that equation set for model calibration and other event simulations.
There are some obvious situations that the SWE should always be used. The following is a list of examples of situations in which the user should generally use the SWE based equations:
1. Highly Dynamic Flood Waves: If the modeler is performing a Dam breaching or flash flood analysis, the flood wave will rise and fall extremely quickly. The change in velocity (acceleration) both spatially and over time will be dramatic. The Diffusion wave equations do not include the local acceleration (changes in velocity with respect to time) and convective acceleration (changes in velocity with respect to distance) terms. These two terms are extremely important in order to model rapidly rising flood waves accurately.
2. Abrupt Contractions and Expansions: In areas where there are very abrupt contractions and expansions, the Full Momentum based equation set will more accurately capture the associated forces through the contraction and expansion of the fluid. This is also due to the inclusion of the convective acceleration term (Which is not included in the Diffusion Wave equations). In general the Full Momentum equation set will compute a higher water surface upstream of the contraction zone.
3. Flat Sloping River Systems: For rivers with very flat slopes (less than 1 ft/mi), gravity and friction may not be the dominant forces acting on a body of water as it travels from one point to another. The forces associated with changes in velocity with respect to time and distance, will play a much more significant role in how a floodwave moves and changes shape in a flat system. Because of this, users should use the Full Momentum equation set instead of then Diffusion Wave equations. As Diffusion wave does not include the acceleration terms with respect to time and space.
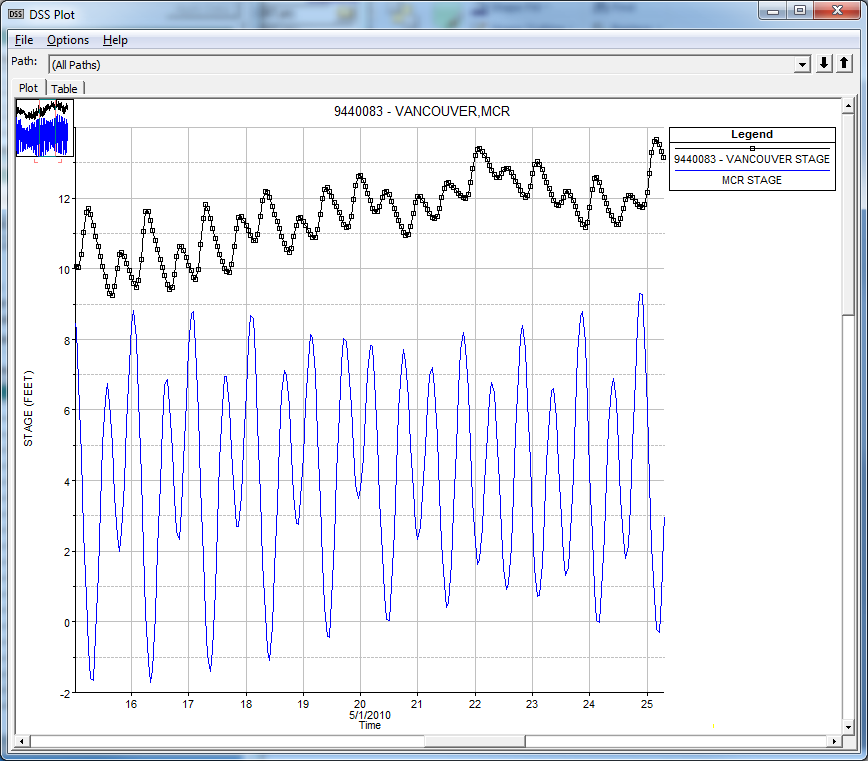
4. Tidally Influenced Conditions: If you are modeling a bay, estuary, or a river that is tidally influenced, then you have to use the full momentum based equation set. The propagation of waves (tide cycle) cannot be modeled with the diffusion wave equations. The ocean tides are dynamic waves that can propagate way up into a river system. There are many examples of where you can see this in gaged river stage data that is very far from the ocean, but still showing a tidal cycle in the stage hydrographs during low flow. Shown below in Figure 4-1 is the Stage data at Vancouver Washington and at the mouth of the Columbia River. As you can see, the tide cycle is evident in the stage data at Vancouver, even though this gage is 106 miles upstream from the mouth of Columbia bay.
5. General Wave Propagation Modeling: If the user needs to model wave propagation due to rapidly opening or closing of gated structures, or wave run-up on a wall or around an object (e.g. bridge piers, buildings, etc…), then the Full Momentum equation set is necessary for this type of modeling.
6. Super Elevation around Bends: If you have a tight bend in either a natural or designed channel, and you want to see if there is any super elevation of the water surface on the outside of the bend, this required the Full Momentum based equation set.
7. Detailed Velocities and Water Surface Elevations at Structures: If you are trying to compute a detailed velocity distribution at or near a hydraulic structure, The full momentum based equation set is more accurate. Some examples are, detailed water surface and velocity through a bridges and around the abutments and piers; Open channel flow through a gate or culvert; detailed velocities though and around a levee breach; detailed water surface and velocities around a building. Note: this type of modeling also requires very small grid cells and small computational time steps.
8. Mixed Flow Regime: In order to accurately model transitions from subcritical to supercritical flow, and from supercritical to subcritical flow (hydraulic jumps), the Full Momentum equation is more accurate.