Green-Ampt

Green and Ampt (1911) directly applied Darcy's law and proposed a simple model for water infiltration into a homogeneous soil with a uniform initial water content. The Green-Ampt (GA) model assumes a homogeneous soil with constant hydraulic conductivity, initial water content, and head at the wetting front (see schematic below). The saturated wetting front is assumes to move downwards as a single piston like displacement.

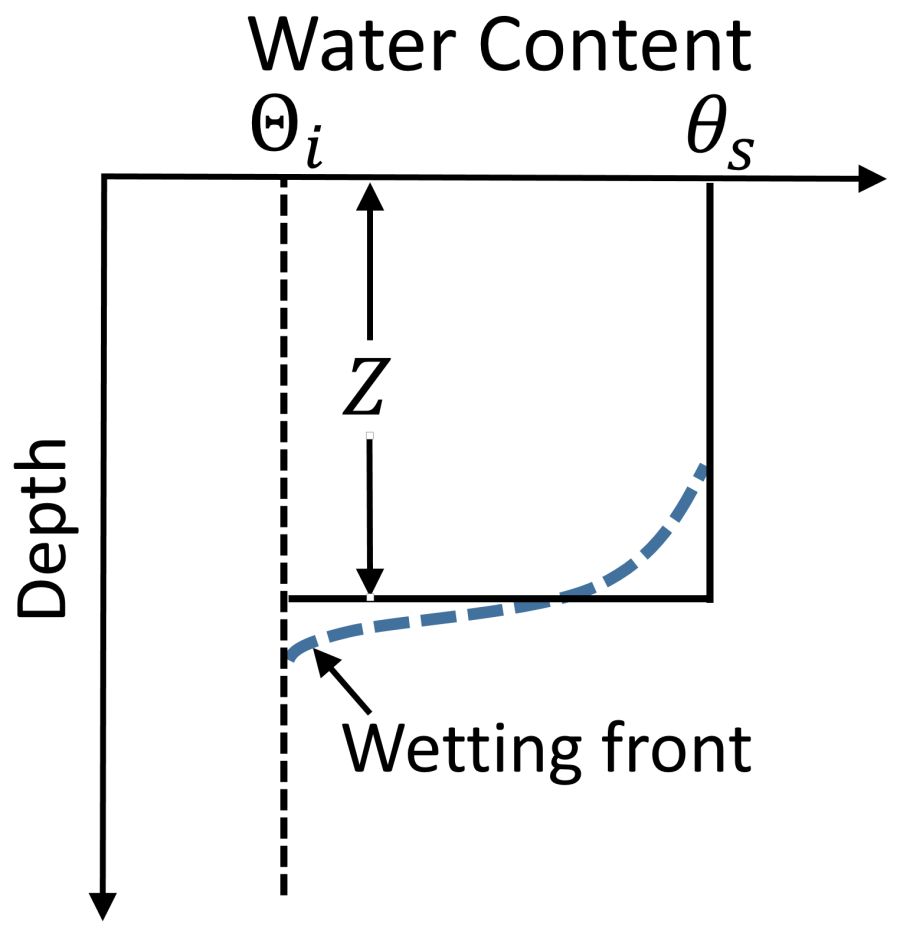
The GA model describes the infiltration process under ponded conditions. Mein and Larson (1973) extended the GA model to determine the time when surface ponding begins under steady rainfall conditions. Chu (1978) further extended the GA model to simulate unsteady rainfall. Lastly, Skaggs and Khaleel (1982) added a water balance equation at the soil surface to compute excess rainfall. The GA model has been widely used in literature to simulate infiltration.

As the water content at the soil surface increases, the GA model movement of the infiltrated water by approximating the wetting front with a piston type displacement. In the GA model, the potential infiltration rate is computed as

where $//<![CDATA[ \begin{array}{l}f_*\end{array} //]]>$ is the potential infiltration rate, $//<![CDATA[ \begin{array}{l}K_S\end{array} //]]>$ is the effective saturated hydraulic conductivity (permeability coefficient), $//<![CDATA[ \begin{array}{l}\Psi\end{array} //]]>$ is average suction across the wetting front, $//<![CDATA[ \begin{array}{l}\theta _d = \theta _S - \theta _i\end{array} //]]>$ is the moisture deficit, $//<![CDATA[ \begin{array}{l}\theta _S\end{array} //]]>$ is the saturated water content, $//<![CDATA[ \begin{array}{l}\theta _i\end{array} //]]>$ is the initial (antecedent) water content, and $//<![CDATA[ \begin{array}{l}F\end{array} //]]>$ is the cumulative infiltration. The actual depth of the wetting front is given by $//<![CDATA[ \begin{array}{l}Z=F/ \theta _d\end{array} //]]>$ . It is noted that the infiltration capacity above is only for the permeable area. The actual infiltration velocity is computed as

where $//<![CDATA[ \begin{array}{l}R\end{array} //]]>$ is the rainfall rate. The cumulative infiltration depth is then computed by solving the ordinary differential equation

The parameters required for the GA model are: (1) the effective saturated hydraulic conductivity, (2) the average suction across the wetting front, (3) the initial water content, and (4) the saturated water content. One advantage of the GA model as compared to other infiltration models, is that its parameters can be estimated directly from soil textural classifications (Rawls et al. 1982, 1983).

In HEC-RAS infiltration is computed during the hydraulic model simulation at the same time step as the hydraulics. Therefore, the computational time step is relatively small for infiltration calculation purposes. The numerical solution of the GA model is designed to be efficient for these relatively small computational time steps. The solution of the GA model begins by using Heun's predictor-corrector method to estimate the cumulative infiltration potential which also provides an absolute error estimate of the potential cumulative infiltration. If the error is larger than an adjustable tolerance of 1×10^-6 ft, then the solution from Heun's method is used as the initial estimate for an implicit solution of the potential cumulative infiltration depth using the Newton-Raphson method (see Chow et al. 1988). For most simulations, the time step is small enough that no Newton-Raphson iterations are needed. If iterations are needed the predictor-corrector scheme produces a very good initial estimate, which reduces the number of iterations needed to converge. The Newton-Raphson method usually converged with 1 to 3 iterations. The combination of the predictor-corrector method with Newton-Raphson method provides a very efficient method when utilizing small computational time steps as in HEC-RAS.

The GA model is appropriate for simulating single rainfall events in which the effects of evapotranspiration and unsaturated gravity-driven flow are not significant. However, in order to simulate longer periods of time with multiple rainfall events, it is important to consider the soil moisture redistribution and evapotranspiration. In order to simulate the recovery of the soil moisture profile between events the Green-Ampt with Redistribution (GAR) method of Ogden and Saghafian (1997) is utilized. The GAR method is based on the earlier framework developed by Smith et al. (1993). The soil moisture profile is represented by one or two rectangular fronts. When rainfall begins, the moisture profile consists of a single saturated front as in the standard Green-Ampt model. A rainfall hiatus period begins when the rainfall is less than the saturated hydraulic conductivity. During the hiatus period the water content of the surface becomes less than the saturated water content. However, the water content profile is assumed to follow a rectangular profile.

During the non-hiatus periods, there may be one or two fronts. If there is one front, it can be saturated or unsaturated. If there are two fronts, one is unsaturated and one is saturated. Infiltration is always calculated using the Green-Ampt equation for the saturated front. If there are two fronts, redistribution only occurs for the unsaturated front. At the beginning of a hiatus period, if there are two fronts, they are merged.

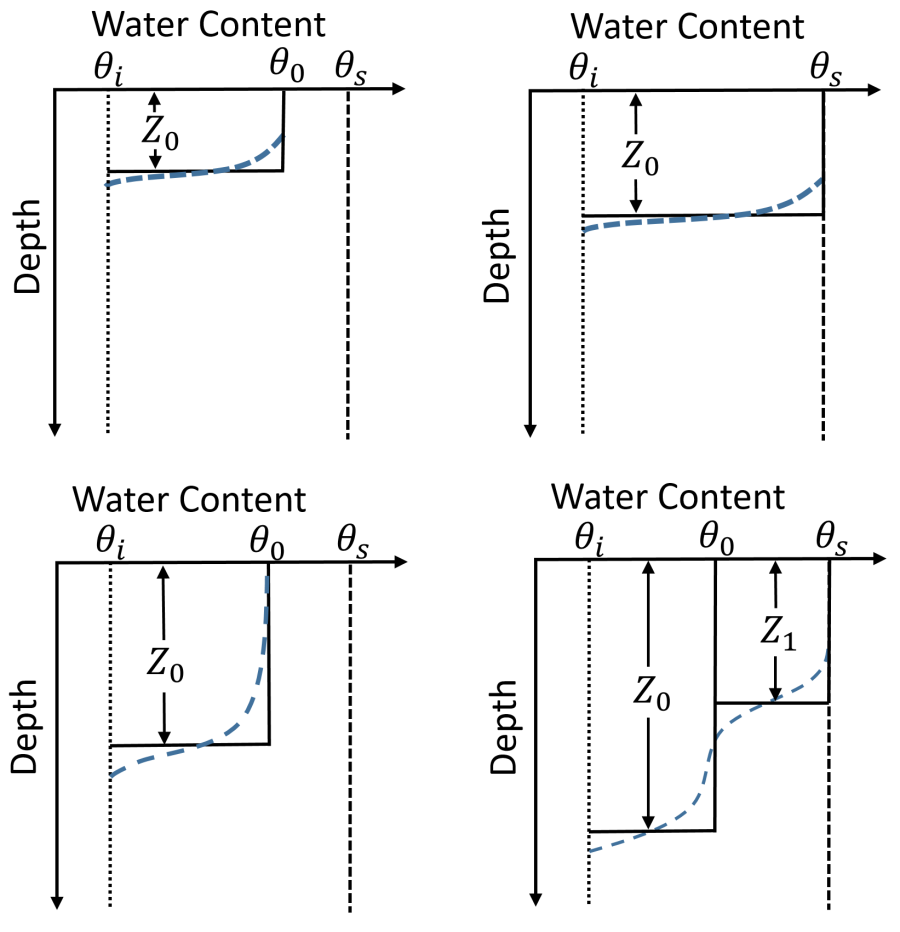
During a rainfall hiatus, the change in soil moisture during the redistribution process is given by (Smith et al. 1993)

where $//<![CDATA[ \begin{array}{l}\theta _0\end{array} //]]>$ is the water content of the unsaturated wetting front, $//<![CDATA[ \begin{array}{l}K_{v,0}\end{array} //]]>$ is the soil evapotranspiration rate, $//<![CDATA[ \begin{array}{l}f\end{array} //]]>$ is the infiltration rate, $//<![CDATA[ \begin{array}{l}G(\theta _i, \theta _0 )\end{array} //]]>$ is integral of the capillary drive through the saturated front, $//<![CDATA[ \begin{array}{l}Z_0 = F_0 / ( \theta _0 - \theta _i )\end{array} //]]>$ is the depth to the wetting front, $//<![CDATA[ \begin{array}{l}K_0 = K(\theta _0)\end{array} //]]>$ is the unsaturated hydraulic conductivity corresponding to a moisture content of $//<![CDATA[ \begin{array}{l}\theta _0\end{array} //]]>$ , $//<![CDATA[ \begin{array}{l}K_i - K(\theta _i )\end{array} //]]>$ is the unsaturated hydraulic conductivity corresponding to the initial moisture content $//<![CDATA[ \begin{array}{l}\theta _i\end{array} //]]>$ , and $//<![CDATA[ \begin{array}{l}K_S = K(\theta _S )\end{array} //]]>$ is saturated hydraulic conductivity. The above equation has been modified here to include the soil evapotranspiration. Evapotranspiration is applied to the unsaturated wetting front unless there is a saturated wetting front, in which case the evapotranspiration is applied to the saturated wetting front.

The cumulative infiltration depth is updated from simple water balance. During a rainfall (non-hiatus) period, there may be one or two vertical wetting fronts; one for the unsaturated region and one for the saturated region. The water balance equations for the two wetting fronts are

where the subscripts indicate the 0 and 1 wetting fronts, $//<![CDATA[ \begin{array}{l}f\end{array} //]]>$ is the infiltration rate, $//<![CDATA[ \begin{array}{l}E_v\end{array} //]]>$ is the evapotranspiration rate, and $//<![CDATA[ \begin{array}{l}K_i\end{array} //]]>$ is the unsaturated hydraulic conductivity corresponding to the initial water content. The infiltration rate is assumed to feed into the second profile only until the two wetting fronts are merge into a single front. However, during hiatus periods, there may only be one unsaturated wetting front. If there are two existing wetting fronts at the start of a hiatus period, the two wetting fronts are merged. When the hiatus period ends, a new saturated wetting front is created and the unsaturated wetting front continues to redistribute.

The capillary drive function $//<![CDATA[ \begin{array}{l}G(\theta _i, \theta _0)\end{array} //]]>$ is computed with the expression by Ogden and Saghafian (1997)

where $//<![CDATA[ \begin{array}{l}\lambda\end{array} //]]>$ is the pore-size distribution index, $//<![CDATA[ \begin{array}{l}\Psi\end{array} //]]>$ average suction across the wetting front, $//<![CDATA[ \begin{array}{l}\Theta = (\theta - \theta _{\lambda} )/( \theta _S - \theta _r)\end{array} //]]>$ is the relative water content in which $//<![CDATA[ \begin{array}{l}\theta _S\end{array} //]]>$ is the saturated water content, $//<![CDATA[ \begin{array}{l}\theta _r\end{array} //]]>$ is the residual water content. The unsaturated hydraulic conductivity is calculated using the relation of Brooks and Corey (1964)

where $//<![CDATA[ \begin{array}{l}K_S =K(\theta _S)\end{array} //]]>$ is the saturated hydraulic conductivity. When simulating the infiltration of the saturated wetting front in the presence of an unsaturated wetting front the water content deficit is computed as

The numerical solution of the GAR model is similar to the GA model except for the fact that there may be two fronts and it also requires the solution of an equation for the unsaturated water content. The unsaturated water content is computed with the 2^nd order Heun's method. If the error estimate of Heun's method is larger than an adjustable tolerance of 1×10^-4 ft than the classic 4^th order Runge-Kutta method is applied as it was in Ogden and Saghafian (1997).

The GAR method requires the same infiltration parameters as the GA method with the addition of the pore-size distribution and the residual water content. A summary of the typical values and ranges for the GA and GAR parameters for different soil textures is shown in the table below.

Table 4. Green-Ampt Parameter Estimates and Ranges based on Soil Texture (from Gowdish and Muñoz-Carpena 2009; Rawls and Brakensiek 1982 and Rawls et al. 1982).