Download PDF
Download page Cross Section Spacing and Hydraulic Properties.
Cross Section Spacing and Hydraulic Properties
Cross-sectional cut lines should be created to capture the entire extent of flooding anticipated by the dam break scenario. As in any hydraulic modeling study, cross sections must be laid out to accurately describe the channel and floodplain geometry. Cross sections are laid out perpendicular to the anticipated flow lines of both the channel and the floodplain, during high flow conditions. There must be enough cross sections to describe the following: contractions and expansions of the channel and/or floodplain; changes in bed slope; changes in roughness; and significant changes in discharge. Cross sections also need to be added immediately upstream and downstream of: tributary inflow locations; dams and other inline structures (weirs, drop structures, or natural drops in the bed profile); bridge and culvert crossings; levees and other types of lateral hydraulic structures. An example of a cross section layout is shown in the figure below. 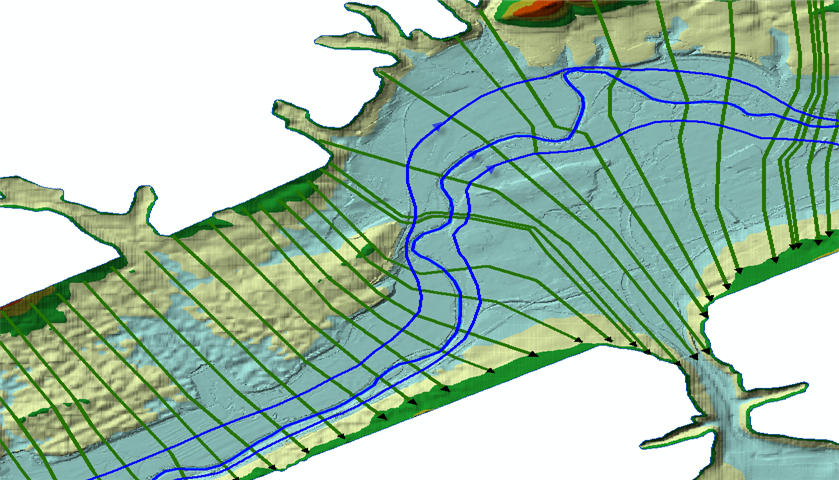
In addition to describing the physical changes and hydraulic structures within the channel and floodplain, there are also numerical considerations for adding or removing cross sections.
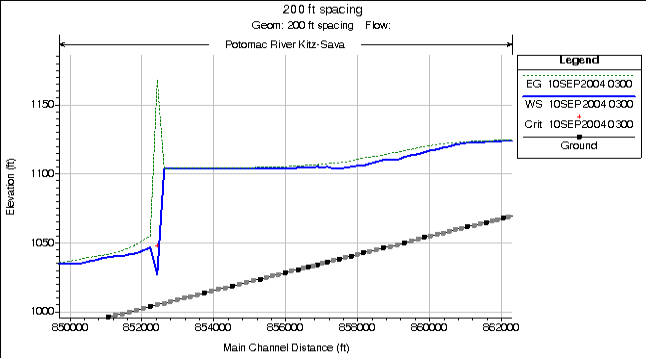
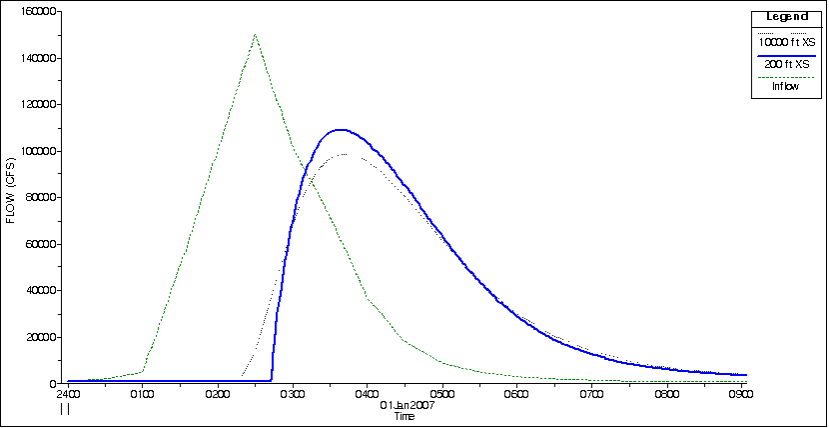
Cross Sections Spaced Too Far Apart. In general, cross sections spaced too far apart will cause additional numerical diffusion of the floodwave, due to the derivatives with respect to distance being averaged over too long of a distance. See an example of artificial numerical diffusion in the figure above. the figure above shows an upstream inflow hydrograph and two downstream hydrographs after they have been routed through the river system. In this example, the channel is a rectangular channel on a constant slope, with a constant Manning's roughness. The only change in the example is the cross section spacing.
Additionally, when cross sections are spaced far apart, and the changes in hydraulic properties are great, the solution can become unstable. Instability can occur when the distance between cross sections is so great that the Courant number becomes much greater than 1.0, and numerical errors grow to the point of the model becoming unstable. Another way to say this is that the cross section spacing is not commensurate with the hydrograph being routed and the computational time step being used (i.e. the cross section spacing is much further than the flood wave can travel within the computational time step being used).
Maximum Cross Section Spacing. A good starting point for estimating maximum cross section spacing are two empirically derived equations by Dr. Danny Fread (Fread, 1993) and P.G. Samuels (Samuels, 1989). These two equations represent very different methods for coming up with spacing. The Samuels equation implies that smaller streams and steeper streams will require tighter cross section spacing. In general, the Samuels equation was derived for typical flood studies, in which the modeler is developing a steady state model for a typical floodplain study of the 2 yr through 100 yr events. For dambreak flood studies, the Samuels equation may be to strict, in that it requires much tighter cross section spacing than needed. Samuels' equation is as follows:
| \displaystyle \Delta x \leq \frac{0.15D}{S_0} |
| Symbol | Description | Units |
|---|---|---|
\Delta x | the cross section spacing distance | ft |
D | the average main channel bankfull depth | ft |
S_0 | the bed slope | ft/ft |
Note
Samuels' equation was derived from data with slopes ranging from 2 - 50 ft/mi.
Dr. Fread's equation implies smaller streams and steeper hydrographs will require tighter cross sections. Fread's equation is one set of three conditions he presented in his paper for determining spacing. It is a theoretical derivation of spacing based on the inherent numerical errors involved with linearizing the St. Venant equations into a four-point implicit finite-difference scheme. The other two involve a check of the change in cross sectional area from one cross section to the next, and the other accounts for changes in slope. Consequently, the spacing determined by Fread's equation may be too coarse, depending on the bed slope changes, the contraction and expansion characteristics and other non-linear data. Dr. Fread's equation is as follows:
| \displaystyle \Delta x \leq \frac{cT_r}{20} |
| Symbol | Description | Units |
|---|---|---|
\Delta x | the cross section spacing distance | ft |
c | the wave speed | ft/s |
T_r | time of rise (from low flow to peak) of the hydrograph | seconds |
Samuels' and Dr. Fread's equations are rough estimates of cross section spacing - a good place to start. However, over time and practice, the modeler should be able to determine a good first estimate based on experience.
Cross Sections Too Close Together. If the cross sections are too close together, then the derivatives with respect to distance may be overestimated, especially on the rising side of the flood wave. This can cause the leading edge of the flood wave to over steepen, to the point at which the model may become unstable. An example of this is shown in the figure below. In this example, the only change made to the model was that cross sections were interpolated at very short intervals (5 feet). If it is necessary to have cross sections at such short intervals, then much smaller time steps will need to be used in order for the numerical computations to solve the equations over such short distances. In general, for most dam break flood studies, cross sections should not be spaced at intervals closer than about 50 feet, unless you can use very small time steps (i.e. a few seconds or less). However, cross sections can be placed at closer distances at hydraulic structures, such as bridges/culverts, dams, and inline weirs, due to the fact that the model does not solve the unsteady flow equations through these structures. Rather it uses hydraulic equations specifically defined for those structures.