Download PDF
Download page Bed Roughness Functions.
Bed Roughness Functions
Because Manning's n values are typically used in HEC-RAS, the uniform flow feature allows for the use of a number of different roughness equations to solve for n. HEC-RAS allows the user to apply any of these equations at any area within a cross section, however, the applicability of each equation should be noted prior to selection. The following bed roughness equations are available:
- Manning Equation
- Keulegan Equation
- Strickler Equation
- Limerinos Equation
- Brownlie Equation
- Soil Conservation Service Equations for Grass Lined Channels
The Manning equation is the basis for the solution of uniform flow in HEC-RAS.
| 1) | \displaystyle Q= \frac{1.486}{n} AR^{2/3}S^{1/2} |
Roughness values solved for using other roughness equations are converted to Manning's n values for use in the computations. One n value or a range of n values is prescribed across the cross section and then the Manning's equation is used to solve for the desired parameter.
Manning Equation:
When choosing the Manning equation method, one n value or a range of n values is prescribed across the cross section and then the Manning's equation is used to solve for the desired parameter.
Keulegan Equation:
The Keulegan (1938) equation is applicable for rigid boundary channel design. Flow is classified according to three types: hydraulically smooth, hydraulically rough, or a transitional zone between smooth and rough. To solve the Keulegan equation, a Nikaradse equivalent sand roughness value, ks must be provided. Values for ks typically range from 1d90 for large stones to 3d90 for sand and gravel with bed forms, where d90 is the representative grain size in which 90% of all particles in the bed are smaller. However, ks values are highly variable and depend also on the types of bed forms, the overall grain distribution, the particle shape factor, and other physical properties. Therefore, unless there is specific data related to the ks value for a given cross section of a river, it is recommended that one of the other roughness equations be chosen. If the discharge, area, hydraulic radius, and slope are known, a ks value can be calculated and then used in the solution of additional discharges, depths, slopes, or widths. EM 1110-2-1601 has a table of suggested ks values for concrete-lined channels.
Van Rijn (1993) defines the three boundary-zone flow regimes as follows:
Hydraulically smooth flow is defined as flow in which the bed roughness elements are much smaller than the thickness of the viscous sublayer and do not affect the velocity distribution (see figure below). This is found when
| 2) | \displaystyle \frac{u_* k_s}{v} \leq 5 |
| Symbol | Description | Units |
|---|---|---|
u_* | current related bed shear velocity | |
v | kinematic viscosity coefficient | |
k_s | equivalent sand roughness value |
Hydraulically rough flow is defined as flow in which a viscous sublayer does not exist and the velocity distribution is not dependent on the viscosity of the fluid (see figure below). This is found when
| 3) | \displaystyle \frac{u_* k_s}{v} \geq 70 |
Transitional flow is where the velocity distribution is affected by viscosity as well as by the bottom roughness.
| 4) | \displaystyle 5 < \frac{u_* k_s}{v} < 70 |
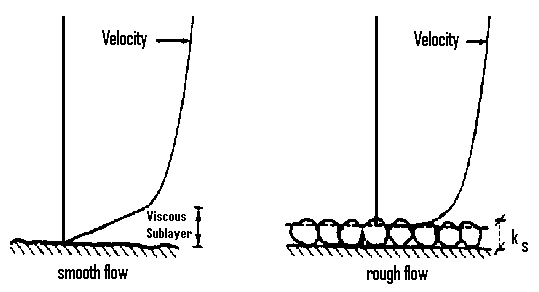
The equation for fully rough flow is
| 5) | \displaystyle C=32.6log_{10} \left( \frac{12.2R}{k_s} \right) |
| Symbol | Description | Units |
|---|---|---|
C | Chezy roughness coefficient | |
R | Hydraulic radius |
And for fully smooth flow
| 6) | \displaystyle C=32.6log_{10} \left( \frac{5.2R_n}{C} \right) |
Where R_n = Reynolds number
Iwagaki (Chow, 1959) found from experimental data that the coefficients 12.2 and 5.2 actually vary with the Froude number. He reasoned that as the Froude number increases, the stability of the free surface diminishes, creating more resistance in the open channel. According to Iwagaki, for fully rough flow, the coefficient 12.2 should be replaced by
| \displaystyle 10 ^{\frac{A_r \sqrt{g}}{32.6}} |
to get
| 7) | \displaystyle C=32.6log_{10} \left[ 10 ^{\frac{A_r \sqrt{g}}{32.6}} \left( \frac{R}{k_s} \right) \right] |
| Symbol | Description | Units |
|---|---|---|
A_s | Coefficient for rough flow that varies with Froude number |
Where:
| 8) | A_s = -27.058 log_{10} (F+9) + 34.289 |
Where: F = Froude number
For fully smooth flow the coefficient 5.2 should be replaced by
\displaystyle \frac{\sqrt{g}}{4} 10 ^{\frac{A_r \sqrt{g}}{32.6}}
to get
| 9) | \displaystyle C=32.6log_{10} \left[ 10 ^{\frac{A_r \sqrt{g}}{32.6}} \left( \frac{\sqrt{g} R}{4C} \right) \right] |
| Symbol | Description | Units |
|---|---|---|
A_s | Coefficient for rough flow that varies with Froude number |
Where:
| 10) | A_s = -24.739 log_{10} (F+10) + 29.349 |
When the flow is in the transitional regime, the Chezy coefficient is just a combination of the equations for smooth and rough flow.
| 11) | \displaystyle C=-32.6 log_{10} \left[ \frac{k_s}{R10 ^{\frac{A_r \sqrt{g}}{32.6}}} + \frac{4C}{\sqrt{g}R_n10 ^{\frac{A_r \sqrt{g}}{32.6}}} \right] |
It should be noted that the data used to develop these equations had Froude numbers ranging from 0.2 to 8.0. Also, the Keulegan method should not be used when the relative roughness (R/k_s) is less than 3. This indicates extremely rough flow, which does not follow the logarithmic velocity distribution from which Keulegan's method is based. HEC-RAS uses (11) for uniform flow computations when the Keulegan method is selected. When the flow is fully rough, the relative roughness term of the equation becomes dominant and the viscous effects (R_n) are relatively small. When the flow is fully smooth, the sublayer viscous effects become dominant and the relative roughness term drops out.
Once the Chezy coefficient is determined, it is converted to a Manning's n value for use in the Manning equation from the following expression:
| 12) | \displaystyle n= \frac{1.486}{C} R^{1/6} |
(U.S. Customary Units)
| \displaystyle n= \frac{1}{C} R^{1/6} |
(S.I. Units)
Strickler Equation
When comparing the relative roughness to a so-called Strickler function, it is found that over a wide range of relative roughness, the variation of the Strickler function, \phi R /k_s is small (Chow, 1959). Because of this relationship, a constant value for the Strickler function can be used to calculate an n value. Strickler assumed this constant value to be 0.0342 when k_s and R are given in feet and when the Nikaradse k_s value is given as the d50 of the bed sediment. Research at WES (Maynard, 1991) has produced different results when the Strickler function is applied to riprap-lined beds. In this case k_s is the bed sediment d90 and the value applied to the Strickler function should depend on the type of calculations when designing channels. For velocity and stone sized calculations, the Strickler function should be 0.0342. For discharge capacity calculations, 0.038 should be used. The following expression converts k_s to an n value.
| 13) | \displaystyle n= \phi \frac{R}{k_s} k_s^{1/6} |
| Symbol | Description | Units |
|---|---|---|
\displaystyle n= \frac{1}{C} R^{1/6} | Nikaradse equivalent sand roughness, =d50 for natural channels and d90 for riprap-lined channels. | ft or m |
\phi R /k_s | Strickler function: 0.0342 for natural channels; 0.0342 for velocity and stone size calculations in riprap design; 0.038 for discharge calculations in riprap design |
Limerinos Equation
Larger grain sizes from coarse sands to cobbles were used by Limerinos (1970) to develop an n-value predictor based on Hydraulic roughness and particle sediment size for mobile bed streams. This method can only be applied to the grain-related upper flow regime, which includes plane bed, antidunes, and chutes and pools. Sand bed streams are applicable provided that the bed form is plane bed (Burkham and Dawdy, 1976). Whether a channel is in upper, lower, or the transitional bed form regime is a function of the localized, or Grain-related Froude Number which is defined as the following:
| 14) | \displaystyle F_g = \frac{V}{\sqrt{(s_s-1)gd_{50}}} |
| Symbol | Description | Units |
|---|---|---|
F_g | Grain-related Froude number | |
V | Average channel velocity | |
s_s | Specific Gravity of sediments particles |
If the bed slope is greater than 0.006, flow is always considered to be in the upper regime. Otherwise, upper and lower regime can be defined as follows
| 15) | \displaystyle \begin{array} 1 F_g > \frac{1.74}{S^{1/3}} & Grain-related \;upper \;Regime \;Flow \\ F_g \leq \frac{1.74}{S^{1/3}} & Grain-related \;lower \;Regime \;Flow \end{array} |
Where: S = Bed Slope
The n-value predictor as defined by Limerinos is:
| 16) | \displaystyle n= \frac{0.0929R^{1/6}}{1.16 + 2.0 log_{10} \left( \frac{R}{d_{84}} \right)} |
| Symbol | Description | Units |
|---|---|---|
R | Hydraulic Radius | |
d_{84} | the particle size for which 84% of all sediments are smaller |
It is important that the Limerinos method be chosen with care. The data ranges at which it applies are relatively small and limited to coarse sands to cobbles in upper regime flow. A particular advantage with the Limerinos method is its apparent accounting for bed form roughness losses. As a consequence, n values computed using Limerinos will normally be significantly higher than those found using Strickler. Burkham and Dawdy showed that the range of relative roughness of the Limerios method is between 600 and 10,000.
Brownlie Equation
Brownlie (1983) developed a method for use with bed forms in both the upper and lower regime. In this method the Strickler function is multiplied by a bed-form roughness, which is a function of the hydraulic radius, the bed slope and the sediment gradation. The resulting equations for lower and upper regime are:
| 17) | \displaystyle \begin{array} 1 \displaystyle n= \left[ 1.6940 \left( \frac{R}{d_{50}} \right) ^{0.1374} S^{0.1112} \sigma ^{0.1605} \right] 0.034 (d_{50}) ^{0.167} & (Lower \;Regime) \\ n= \left[ 1.0213\left( \frac{R}{d_{50}} \right) ^{0.0662} S^{0.0395} \sigma ^{0.1282} \right] 0.034 (d_{50}) ^{0.167} & (Upper \;Regime) \end{array} |
| Symbol | Description | Units |
|---|---|---|
\sigma | the geometric standard deviation of the sediment mixture |
Where:
| 18) | \displaystyle \sigma =0.5 \left( \frac{d_{84} +d_{50}}{d_{50} +d_{16}} \right) |
In actuality, the transition between the upper and lower regimes does not occur at one point, but rather over a range of hydraulic radii. Within this range, there are actually two valid solutions (a lower and an upper regime solution) because the transition is initiated at different discharges depending on whether the occurrence is on the rising end or falling end of the hydrograph. HEC-RAS will solve for both and when there are two solutions, a message box will appear that requests the user to select which regime to solve for. A general rule of thumb is to use the upper regime for the rising end of the hydrograph and the lower regime for the falling end of the hydrograph (see figure below).
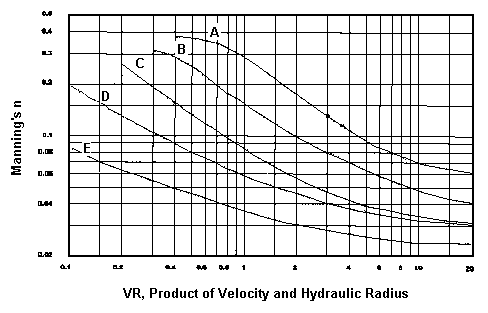
Table 12-1 Characteristics of Grass Cover
Grass Type | Cover | Condition |
|---|---|---|
A | Weeping lovegrass………………...... | Excellent Stand, tall (average 30 in) |
B | Kudzu……………………………............. | Very dense growth, uncut |
C | Crabgrass……………………….......... | Fair stand, uncut (10 to 48 in) |
D | Bermudagrass…………………….... | Good stand, cut to 2.5 in height |
E | Bermudagrass……………………..... | Good stand, cut to 1.5 in height |
Soil Conservation Service Grass Cover
The Soil Conservation Service (SCS, US Department of Agriculture, 1954) has developed five curves that define the respective roughness as a function of the product of velocity and hydraulic radius. Each curve, A through E, represents a different type of grass cover, all of which are presented in Table 12-1. The ranges over which these curves apply can be seen in the figure above.
Selection of Roughness Equation
Each of the roughness equations described above have limitations to their applicability. Selection of one or more methods should be chosen based on stream characteristics with knowledge of the development of the chosen method(s) to better determine the appropriate roughness values to use. For example, vegetation roughness and bank angle typically do not permit the movement of bed load along the face of the banks, therefore bed roughness predictors such as Limerinos and Brownlie should not be used at those locations in the cross section. For this reason, HEC-RAS only allows the user to define one sediment gradation, which should be applied to the main channel bed only. In addition, the equations used to solve for Manning's n values are typically based on a representative grain diameter and hydraulic parameters. Other roughness affects such as vegetation, temperature, planform, etc., are not accounted for. The following table (Table 12-2) gives a general idea of the limitations and applicabilities of each roughness predictor.
Table 12-2 Data Range and Applicabilities of Roughness Predictors
Equation | Data Range | Applicability |
|---|---|---|
Mannings | Typically .01<n<.5 | All. However, n-values do not have the ability to directly vary with Hydraulic Radius |
Keulegan | Froude number 0.2<F<8.0 | In streams where the relative roughness value, R/ks >= 3 |
Strickler | R/ks >=1 | Natural channels for uniform flow computations. |
Limerinos | 1.5mm<d84<250mm | Coarse sand to large cobbles. Only upper regime flow. Mobile beds. Main channel bed only. |
Brownlie | Upper, lower, and transitional regimes. Mobile beds. Main channel bed only. | |
SCS Grass Curves | 0.1 to 0.4<VR<20 | Grass cover. See Table 12-1 |