Face-Tangential Velocity

In HEC-RAS 2D, the current velocities are solved normal to the faces. The face tangential velocity is reconstructed using what is referred to as a double-C stencil which is shown in the Figure below.

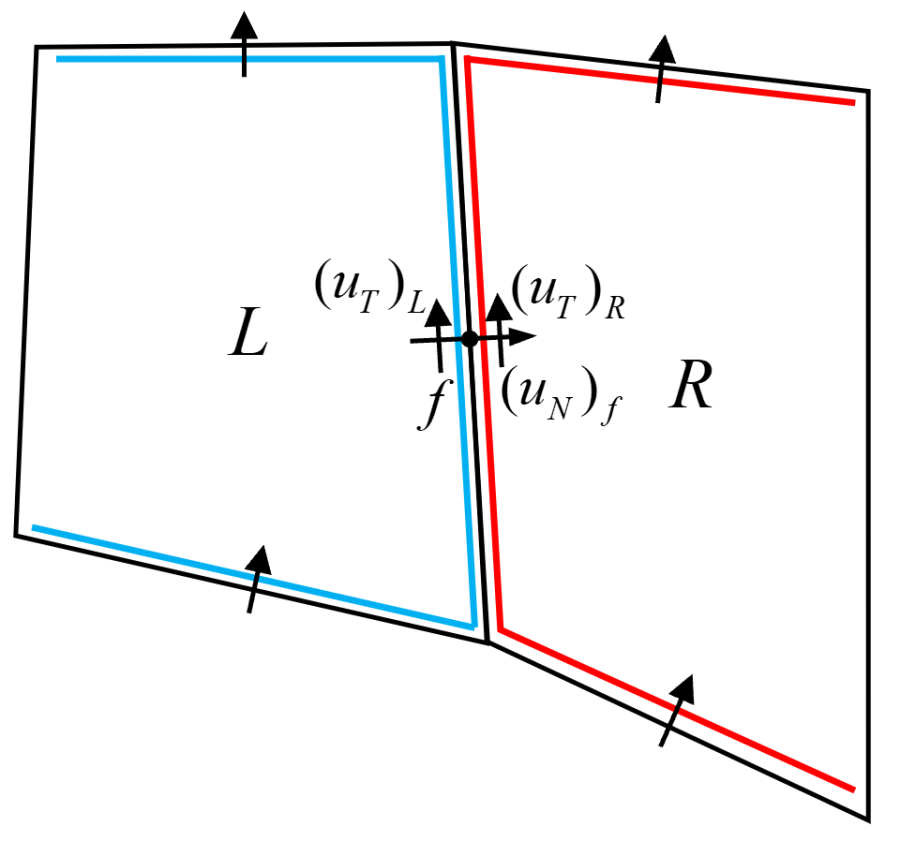
Figure 1. Double-C stencil used for computing the face tangential velocity.

The weighted least-squares gradient approach is linearly exact and works for any mesh topology. The method solves two least-squares problems for every face:

1)	$\begin{array}{l}\displaystyle \displaystyle S_{R/L} = \sum_{k \epsilon \text{K} ( \text{R}(f) \| \text{L}(f) ) }^3 \left( \textbf{V} _{R\|L} \cdot \textbf{n}_k - (u_N)_k \right) ^2\end{array}$

where $\begin{array}{l}\textbf{n}_k = (n_{k,1}, n_{k,2})^T\end{array}$ is the face-normal unit vector and $\begin{array}{l}(u_N)_k\end{array}$ is the face-normal velocity at face k. The velocity $\begin{array}{l}\textbf{V}_{R|L}\end{array}$ represents the right or left reconstructed least-squares velocity vectors $\begin{array}{l}\textbf{V}_{R}\end{array}$ and $\begin{array}{l}\textbf{V}_{L}\end{array}$ , respectively. Of the reconstructed velocity vectors, only the tangential velocity is utilized, because the face-normal velocity is known. These are computed as $\begin{array}{l}(u_N)_k = \textbf{V} _{R|L} \cdot \textbf{t}_k\end{array}$ , in which $\begin{array}{l}\textbf{t}_k\end{array}$ is the unit vector tangential to face k. The solution to the least-squares problem is:

2)	$\begin{array}{l}\displaystyle \displaystyle (u_T)_{R/L} = \frac{1}{\Delta} \left[ \left( a_{1,1} n_{f,1} + a_{1,2} n_{f,2} \right) b_2 - \left( a_{2,1} n_{f,1} + a_{2,2} n_{f,2} \right) b_1 \right]\end{array}$

in which the coefficients are:

$\begin{array}{l}\displaystyle a_{1,1} = \sum_k n_{k,1}^2\end{array}$ , $\begin{array}{l}\displaystyle a_{2,2} = \sum_k n_{k,2}^2\end{array}$ , $\begin{array}{l}\displaystyle a_{1,2} = a_{2,1} = \sum_k n_{k,1} n_{k,1}\end{array}$ , $\begin{array}{l}\Delta = a_{1,1} a_{2,2} - a_{1,2} a_{2,1}\end{array}$ , $\begin{array}{l}\displaystyle b_1 = \sum_k n_{k,1} (u_N)_k\end{array}$ , $\begin{array}{l}\displaystyle b_1 = \sum_k n_{k,2} (u_N)_k\end{array}$

If two cells are hydraulically connected, the left and right tangential velocities are averaged to compute face tangential velocity as the arithmetic average:

3)	$\begin{array}{l}\displaystyle \displaystyle (u_T)_f = \frac{(u_T)_R + (u_T)_L}{2}\end{array}$