HEC-RAS is capable of modeling radial gates (often called tainter gates), vertical lift gates (sluice gates), and overflow gates. The equations used to model the gate openings can handle both submerged and unsubmerged conditions at the inlet and the outlet of the gates. When the gates are opened to an elevation greater than the upstream water surface elevation, the program automatically switches to modeling the flow through the gates as weir flow. When the upstream water surface is greater than or equal to 1.25 times the height of the gate opening (with respect to the gate's spillway crest), the weir flow equation are applied. When the upstream water surface is between 1.0 and 1.25 times the gate opening, the flow is in a zone of transition between weir flow and gate flow. The program computes the upstream head with both equations and then calculates a linear weighted average of the two values (this is an iterative process to obtain the final headwater elevation for a flow in the transition range). When the upstream water surface is equal to or less than 1.0 times the gate opening, then the flow through the gate opening is calculated as weir flow.
A summary of types of flow through gated spillways is provided below. The form of the equations discussed is simplified to assume a rectangular shape where flow area can be computed as the height of the gate opening times the gate width.
Free Flow (Weir Flow)
Free flow occurs when the Energy Grade Line is below the bottom of the gate. Flow is computed using the Weir Flow equation shown below, where the Energy Grade Line is used to compute the "head" above the sill of the weir, Headwater Depth (H). Additional considerations are evaluated for ogee crested, broad crested, and sharp crested shapes. Submergence is also considered. The simple form of the weir equation is shown below.
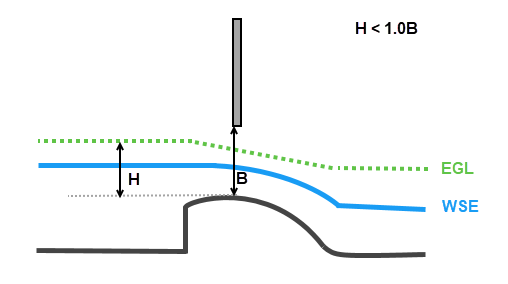
The transition to gate flow occurs when the Energy Grade Line hits the bottom of the gate at which point the gate is evaluated for sluice flow and/or orifice flow. The transition from weir flow to gate flow occurs when the Headwater Depth (H) divided by the gate opening (B) is between 1.0 and 1.25. Flow is computed as a linear transition from weir flow to sluice flow in this range.
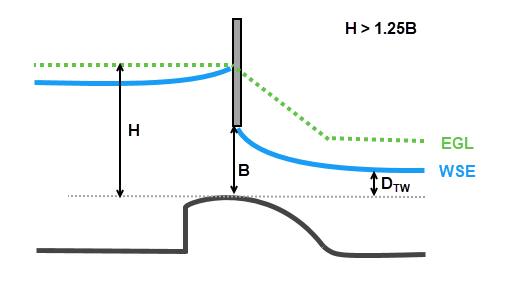
Sluice Flow (Free Orifice Flow)
Sluice gate flow occurs when the Headwater depth (H) (as defined by the difference in Energy Grade Line above the weir) is greater than 1.25 times the gate opening height (B). Further, the submergence defined as the Tailwater Depth (DTW) divided by the Headwater Depth (H) is less than 0.67. The simple form of the sluice gate equation is shown below.
Orifice Flow (Submerged Orifice Flow)
Orifice Flow occurs when the Headwater Depth (H) is greater than 1.25 times the gate opening height (B). Further, the submergence defined as the Tailwater Depth (DTW) divided by the Headwater Depth (H) is greater than 0.8. The orifice equation is shown below, where Ho is defined by the difference between the upstream Energy Grade Line and the downstream Water Surface Elevation.
Transition Flow (Sluice to Orifice)
Transition flow occurs when submergence (defined as Tailwater Depth (DTW) divided by Headwater Depth (H)) is between 0.67 and 0.8. Flow is computed as a linear transition from sluice flow to orifice flow. A simplified form of the orifice equation during transition flow is shown below. The head (Ht) used for computing flow through the transition zone is defined as the difference between the upstream Energy Grade Line and the downstream Water Surface Elevation.
