High Flow Computations

The HEC-RAS program has the ability to compute high flows (flows that come into contact with the maximum low chord of the bridge deck) by either the Energy equation (standard step method) or by using separate hydraulic equations for pressure and/or weir flow. The two methodologies are explained below.

Energy Equation (standard step method). The energy-based method is applied to high flows in the same manner as it is applied to low flows. Computations are based on balancing the energy equation in three steps through the bridge. Energy losses are based on friction and contraction and expansion losses. Output from this method is available at the cross sections inside the bridge as well as outside.
As mentioned previously, friction losses are based on the use of Manning's equation. Guidance for selecting Manning's n values is provided in "Basic Data Requirements" of this manual. Contraction and expansion losses are based on a coefficient times the change in velocity head. Guidance on the selection of contraction and expansion coefficients has also been provided in "Basic Data Requirements", as well as previous sections of this chapter.

The energy-based method performs all computations as though they are open channel flow. At the cross sections inside the bridge, the area obstructed by the bridge piers, abutments, and deck is subtracted from the flow area and additional wetted perimeter is added. Occasionally the resulting water surfaces inside the bridge (at sections BU and BD) can be computed at elevations that would be inside of the bridge deck. The water surfaces inside of the bridge reflect the hydraulic grade line elevations, not necessarily the actual water surface elevations. Additionally, the active flow area is limited to the open bridge area.

Pressure and Weir Flow Method. A second approach for the computation of high flows is to utilize separate hydraulic equations to compute the flow as pressure and/or weir flow. The two types of flow are presented below.

Pressure Flow Computations:

Pressure flow occurs when the flow comes into contact with the low chord of the bridge. Once the flow comes into contact with the upstream side of the bridge, a backwater occurs and orifice flow is established. The program will handle two cases of orifice flow; the first is when only the upstream side of the bridge is in contact with the water; and the second is when the bridge opening is flowing completely full. The HEC-RAS program will automatically select the appropriate equation, depending upon the flow situation. For the first case (see the figure below), a sluice gate type of equation is used (FHWA, 1978):

1)	$\begin{array}{l}\displaystyle \displaystyle Q=C_d A_{BU} \sqrt{2g} \left[ Y_3 - \frac{Z}{2} + \frac{a_3V^2_3}{2g} \right] ^{1/2}\end{array}$

Symbol	Description	Units
$\begin{array}{l}Q\end{array}$	Total discharge through the bridge opening
$\begin{array}{l}C_d\end{array}$	Coefficients of discharge for pressure flow
$\begin{array}{l}A_{BU}\end{array}$	Net area of the bridge opening at section BU
$\begin{array}{l}Y_3\end{array}$	Hydraulic depth at section 3 by subtracting the mean bed elevation at the bridge from the WSEL at section 3
$\begin{array}{l}Z\end{array}$	Vertical distance from maximum bridge low chord to the mean river bed elevation at section BU

Note that the mean bed elevation at the bridge used to compute Y3 and Z is calculated by subtracting the hydraulic depth of the bridge opening from the low chord elevation.

The discharge coefficient C_d, can vary depending upon the depth of water upstream. Values for C_d range from 0.27 to 0.5, with a typical value of 0.5 commonly used in practice. The user can enter a fixed value for this coefficient or the program will compute one based on the amount that the inlet is submerged. A diagram relating C_d to Y₃/Z is shown in the figure below.

Coefficient of discharge for sluice gate type flow

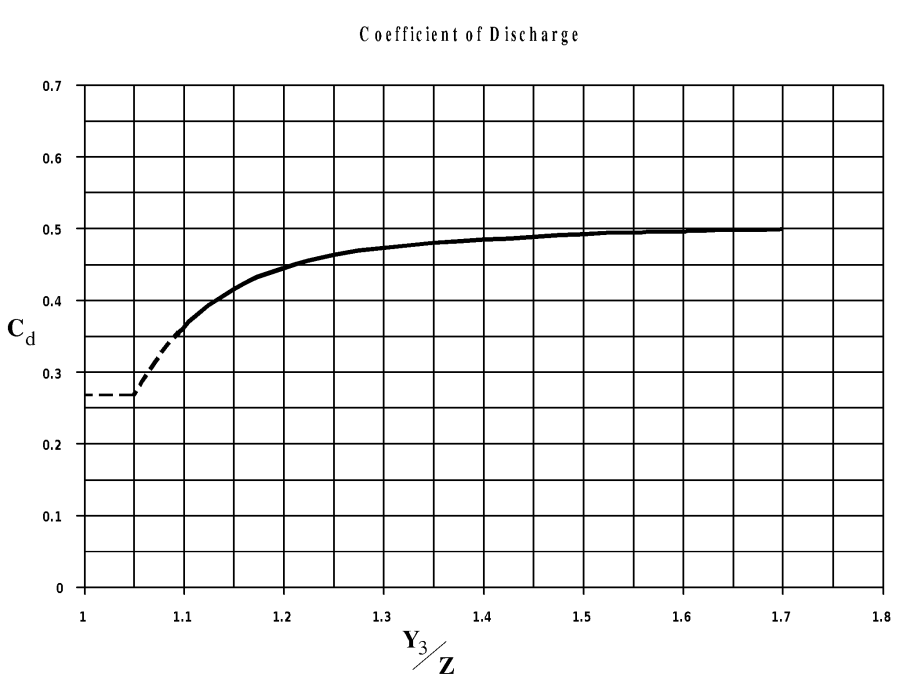
As shown in Figure 5-5, the limiting value of Y₃/Z is 1.1. There is a transition zone somewhere between Y₃/Z = 1.0 and 1.1 where free surface flow changes to orifice flow. The type of flow in this range is unpredictable, and the sluice gate equation (above) is not applicable.

In the second case, when both the upstream and downstream side of the bridge are submerged, the standard full flowing orifice equation is used (see the figure below). This equation is as follows:

2)	$\begin{array}{l}\displaystyle Q=CA \sqrt{2gH}\end{array}$

Symbol	Description	Units
$\begin{array}{l}C\end{array}$	Coefficient of discharge for fully submerged pressure flow. Typical value of C is 0.8.
$\begin{array}{l}H\end{array}$	The difference between the energy gradient elevation upstream and the water surface elevation downstream.
$\begin{array}{l}A\end{array}$	Net area of the bridge opening.

Typical values for the discharge coefficient C range from 0.7 to 0.9, with a value of 0.8 commonly used for most bridges. The user must enter a value for C whenever the pressure flow method is selected. The discharge coefficient C can be related to the total loss coefficient, which comes from the form of the orifice equation that is used in the HEC-2 computer program (HEC, 1991):

3)	$\begin{array}{l}\displaystyle \displaystyle Q=A \sqrt{\frac{2gH}{K}}\end{array}$

Where: $\begin{array}{l}K\end{array}$ = Total loss coefficient

The conversion from to is as follows:

4)	$\begin{array}{l}\displaystyle \displaystyle C= \sqrt{\frac{1}{K}}\end{array}$

The program will begin checking for the possibility of pressure flow when the computed low flow energy grade line is above the maximum low chord elevation at the upstream side of the bridge. Once pressure flow is computed, the pressure flow answer is compared to the low flow answer, the higher of the two is used. The user has the option to tell the program to use the water surface, instead of energy, to trigger the pressure flow calculation.

Weir Flow Computations:

Flow over the bridge, and the roadway approaching the bridge, is calculated using the standard weir equation (see the figure below):

5)	$\begin{array}{l}\displaystyle Q=CLH^{3/2}\end{array}$

Symbol	Description	Units
$\begin{array}{l}Q\end{array}$	Total flow over the weir
$\begin{array}{l}C\end{array}$	Coefficients of discharge for weir flow
$\begin{array}{l}L\end{array}$	Effective length of the weir
$\begin{array}{l}H\end{array}$	Difference between energy upstream and road crest

The approach velocity is included by using the energy grade line elevation in lieu of the upstream water surface elevation for computing the head, H.

Under free flow conditions (discharge independent of tailwater) the coefficient of discharge C, ranges from 2.5 to 3.1 (1.38 1.71 for metric) for broad-crested weirs depending primarily upon the gross head on the crest (C increases with head). Increased resistance to flow caused by obstructions such as trash on bridge railings, curbs, and other barriers would decrease the value of C.

Tables of weir coefficients, C, are given for broadcrested weirs in King's Handbook (King, 1963), with the value of C varying with measured head H and breadth of weir. For rectangular weirs with a breadth of 15 feet and a H of 1 foot or more, the given value is 2.63 (1.45 for metric). Trapezoidal shaped weirs generally have a larger coefficient with typical values ranging from 2.7 to 3.08 (1.49 to 1.70 for metric).

"Hydraulics of Bridge Waterways" (FHWA, 1978) provides a curve of C versus the head on the roadway. The roadway section is shown as a trapezoid and the coefficient rapidly changes from 2.9 for a very small H to 3.03 for H = 0.6 feet. From there, the curve levels off near a value of 3.05 (1.69 for metric).

With very little prototype data available, it seems the assumption of a rectangular weir for flow over the bridge deck (assuming the bridge can withstand the forces) and a coefficient of 2.6 (1.44 for metric) would be reasonable. If the weir flow is over the roadway approaches to the bridge, a value of 3.0 (1.66 for metric) would be consistent with available data. If weir flow occurs as a combination of bridge and roadway overflow, then an average coefficient (weighted by weir length) could be used.

For high tailwater elevations, the program will automatically reduce the amount of weir flow to account for submergence on the weir. Submergence is defined as the depth of water above the minimum weir elevation on the downstream side (section 2) divided by the height of the energy gradeline above the minimum weir elevation on the upstream side (section 3). The reduction of weir flow is accomplished by reducing the weir coefficient based on the amount of submergence. Submergence corrections are based on a trapezoidal weir shape or optionally an ogee spillway shape. The total weir flow is computed by subdividing the weir crest into segments, computing L, H, a submergence correction, and a Q for each section, then summing the incremental discharges. The submergence correction for a trapezoidal weir shape is from "Hydraulics of Bridge Waterways" (Bradley, 1978). Figure 5-8 shows the relationship between the percentage of submergence and the flow reduction factor.

When the weir becomes highly submerged the program will automatically switch to calculating the upstream water surface by the energy equation (standard step backwater) instead of using the pressure and weir flow equations. The criteria for when the program switches to energy based calculations is user controllable. A default maximum submergence is set to 0.98 (98 percent).

Factor for reducing weir flow for submergence