The suspension of a sediment particle is initiated once the bed-level shear velocity approaches the same magnitude as the fall velocity of that particle. The particle will remain in suspension as long as the vertical components of the bed-level turbulence exceed that of the fall velocity. Therefore, the determination of suspended sediment transport relies heavily on the particle fall velocity.
Within HEC-RAS, the method for computing fall velocity can be selected by the user. Three methods are available and they include Toffaleti (1968), Van Rijn (1993), and Rubey (1933). Additionally, the default can be chosen in which case the fall velocity used in the development of the respective sediment transport function will be used in RAS. Typically, the default fall velocity method should be used, to remain consistent with the development of the sediment transport function, however, if the user has specific information regarding the validity of one method over the other for a particular combination of sediment and hydraulic properties, computing with that method is valid. The shape factor (sf) is more important for medium sands and larger. Toffaleti used a sf of 0.9, while Van Rijn developed his equations for a sf of 0.7. Natural sand typically has a sf of about 0.7. The user is encouraged to research the specific fall velocity method prior to selection.
| 1) |
\displaystyle sf= \frac{c}{\sqrt{ab}} |
| Symbol | Description | Unit |
|---|
| Length of particle along the longest axis perpendicular to the other two axes. |
|
| Length of particle along the intermediate axis perpendicular to other two axes. |
|
| Length of particle along the short axis perpendicular to other two axes. |
|
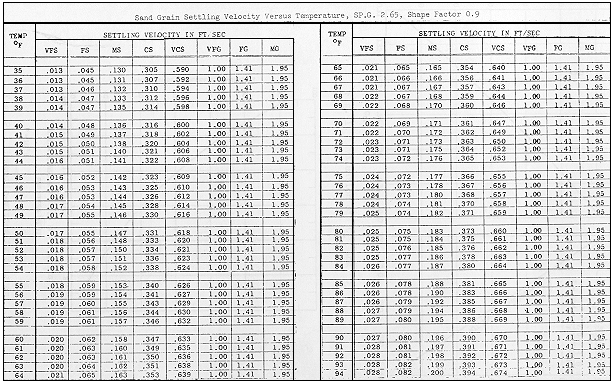
Toffaleti: (Toffaleti, 1968). Toffaleti presents a table of fall velocities with a shape factor of 0.9 and specific gravity of 2.65. Different fall velocities are given for a range of temperatures and grain sizes, broken up into American Geophysical Union standard grain size classes from Very Fine Sand (VFS) to Medium Gravel (MG). Toffaleti's fall velocities are presented in Table 12-6.
Van Rijn: (Van Rijn, 1993). Van Rijn approximated the US Inter-agency Committee on Water Resources' (IACWR) curves for fall velocity using non-spherical particles with a shape factor of 0.7 in water with a temperature of 20oC. Three equations are used, depending on the particle size:
| 2) |
\displaystyle \omega = \frac{(s-1)gd}{18 \nu} \; \; 0.001 \;< \;d \;< \;0.1 \;mm |
| 3) |
\displaystyle \omega = \frac{10 \nu}{d} \left[ \left(1+ \frac{0.01(s-1)gd}{\nu ^2} \right) ^{0.5} -1 \right] \; \;0.1 \;< \;d \;<1 \;mm |
| 4) |
\displaystyle \omega =1.1 \left[ (s-1)gd \right] ^{0.5} \; \;d \; \geq \;1 \;mm |
| Symbol | Description | Units |
|---|
| Particle fall velocity |
|
| Kinematic viscosity |
|
| Specific gravity of particles |
|
| Particle diameter |
|
Table 12-6 Fall Velocity (Toffaleti, 1968)
Rubey: (Rubey, 1933). Rubey developed an analytical relationship between the fluid, sediment properties, and the fall velocity based on the combination of Stoke's law (for fine particles subject only to viscous resistance) and an impact formula (for large particles outside the Stoke's region). This equation has been shown to be adequate for silt, sand, and gravel grains. Rubey suggested that particles of the shape of crushed quartz grains, with a specific gravity of around 2.65, are best applicable to the equation. Some of the more cubic, or uniformly shaped particles tested, tended to fall faster than the equation predicted. Tests were conducted in water with a temperature of 16 ^{\circ} Celsius.
| 5) |
\displaystyle \omega = F_1 \sqrt{(s-1)gd_s} |
in which
| 6) |
\displaystyle F_1 = \sqrt{\frac{2}{3} + \frac{36 \nu ^2}{gd^3 (s-1)}} - \sqrt{\frac{36 \nu ^2}{gd^3(s-1)}} |