Applications of the Momentum Equation

Whenever the water surface passes through critical depth, the energy equation is not considered to be applicable. The energy equation is only applicable to gradually varied flow situations, and the transition from subcritical to supercritical or supercritical to subcritical is a rapidly varying flow situation. There are several instances when the transition from subcritical to supercritical and supercritical to subcritical flow can occur. These include significant changes in channel slope, bridge constrictions, drop structures and weirs, and stream junctions. In some of these instances empirical equations can be used (such as at drop structures and weirs), while at others it is necessary to apply the momentum equation in order to obtain an answer.

Within HEC-RAS, the momentum equation can be applied for the following specific problems: the occurrence of a hydraulic jump; low flow hydraulics at bridges; and stream junctions. In order to understand how the momentum equation is being used to solve each of the three problems, a derivation of the momentum equation is shown here. The application of the momentum equation to hydraulic jumps and stream junctions is discussed in detail in "Overview of Optional Capabilities". Detailed discussions on applying the momentum equation to bridges can be found in "Modeling Bridges".

The momentum equation is derived from Newton's second law of motion:

Force = Mass x Acceleration (change in momentum)

1)	$\begin{array}{l}\displaystyle \sum F_x=ma\end{array}$

Applying Newton's second law of motion to a body of water enclosed by two cross sections at locations 1 and 2 (see figure below), the following expression for the change in momentum over a unit time can be written:

2)	$\begin{array}{l}\displaystyle P_2 - P_1+ W_x - F_f=Q\rho\Delta V_x\end{array}$

Symbol	Description	Units
$\begin{array}{l}P\end{array}$	Hydrologic pressure force at locations 1 and 2.
$\begin{array}{l}W_z\end{array}$	Force due to the weight of water in the X direction.
$\begin{array}{l}F_f\end{array}$	Force due to external friction losses from 2 and 1
$\begin{array}{l}W\end{array}$	Discharge
$\begin{array}{l}\rho\end{array}$	Density of water
$\begin{array}{l}\Delta V_z\end{array}$	Change on velocity from 2 to 1, in the X direction.

Application of the Momentum Principle

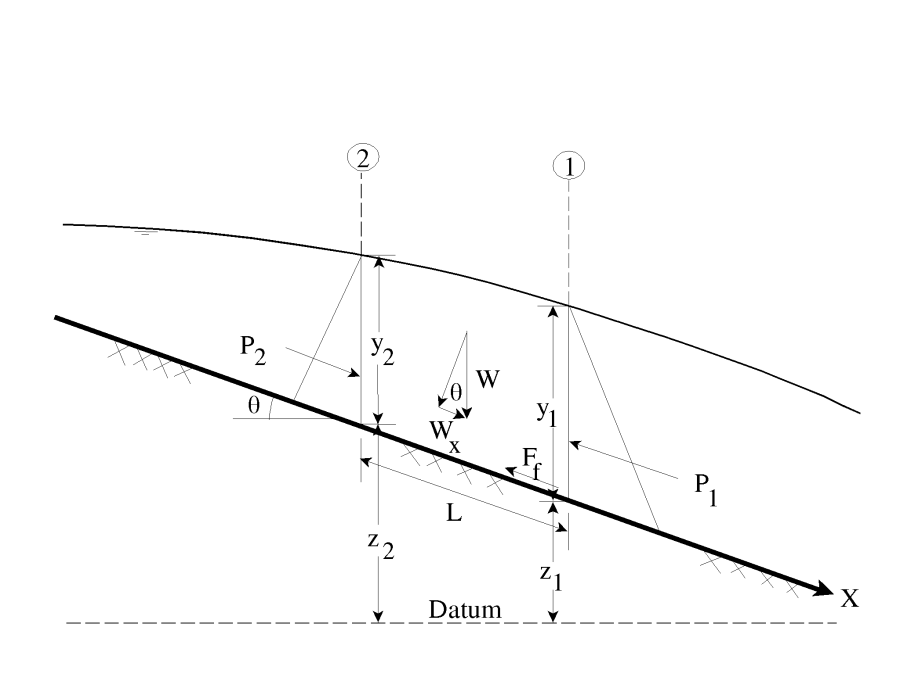
Hydrostatic Pressure Forces:

The force in the $\begin{array}{l}X\end{array}$ direction due to hydrostatic pressure is:

3)	$\begin{array}{l}\displaystyle P=\gamma A \overline{Y} cos\theta\end{array}$

The assumption of a hydrostatic pressure distribution is only valid for slopes less than 1:10. The $\begin{array}{l}cos \theta\end{array}$ for a slope of 1:10 (approximately 6 degrees) is equal to 0.995. Because the slope of ordinary channels is far less than 1:10, the cos θ correction for depth can be set equal to 1.0 (Chow, 1959). Therefore, the equations for the hydrostatic pressure force at sections 1 and 2 are as follows:

4)	$\begin{array}{l}\displaystyle P_1=\gamma A_1 \overline{Y}_1\end{array}$

5)	$\begin{array}{l}\displaystyle P_2=\gamma A_2 \overline{Y}_2\end{array}$

Symbol	Description	Units
$\begin{array}{l}\gamma\end{array}$	Unit weight of water
$\begin{array}{l}A_1\end{array}$	Wetted area of the cross section at locations 1 and 2
$\begin{array}{l}\overline{Y}_1\end{array}$	Depth measured from water surface to the centroid of the cross sectional area at locations 1 and 2.

Weight of Water Force:

Weight of water = (unit weight of water) x (volume of water)

6)	$\begin{array}{l}\displaystyle W=\gamma \left( \frac{A_1+A_2}{2} \right) L\end{array}$

7)	$\begin{array}{l}\displaystyle W_x=W \times sin\theta\end{array}$

8)	$\begin{array}{l}\displaystyle sin\theta = \frac{z_2-z_1}{L} = S_0\end{array}$

9)	$\begin{array}{l}\displaystyle W_x = \gamma \left( \frac{A_1+A_2}{L} \right) LS_0\end{array}$

Symbol	Description	Units
$\begin{array}{l}L\end{array}$	Distance between sections 1 and 2 along the X axis
$\begin{array}{l}S_0\end{array}$	Slope of the channel, based on mean bed elevations
$\begin{array}{l}z_i\end{array}$	Mean bed elevation at locations 1 and 2

Force of External Friction:

10)	$\begin{array}{l}\displaystyle F_f=\tau \overline{P}L\end{array}$

Symbol	Description	Units
$\begin{array}{l}\tau\end{array}$	Shear stress
$\begin{array}{l}\overline{P}\end{array}$	Average wetted perimeter between sections 1 and 2

11)	$\begin{array}{l}\displaystyle \tau = \gamma \overline{R} \overline{S}_f\end{array}$

Symbol	Description	Units
$\begin{array}{l}\overline{R}\end{array}$	Average hydraulic radius (R = A/P)
$\begin{array}{l}\overline{S}_f\end{array}$	Slope of the energy grade line (friction slope)

12)	$\begin{array}{l}\displaystyle F_f= \gamma \frac{\overline{A}}{\overline{P}}\overline{S}_f \overline{P}L\end{array}$

13)	$\begin{array}{l}\displaystyle F_f=\gamma \frac{A_1+A_2}{2} \overline{S}_fL\end{array}$

Mass times Acceleration:

14)	$\begin{array}{l}\displaystyle ma=Q\rho \Delta V_x\end{array}$

$\begin{array}{l}\rho = \frac{\gamma}{g}\end{array}$ and $\begin{array}{l}\Delta V_x = \left( \beta_1V_1 - \beta_2V_2 \right)\end{array}$

15)	$\begin{array}{l}\displaystyle ma=\frac{Q\gamma}{g} \left( \beta_1V_1 - \beta_2V_2 \right)\end{array}$

Symbol	Description	Units
$\begin{array}{l}\beta\end{array}$	momentum coefficient that accounts for a varying velocity distribution in irregular channel

Substituting Back into (2), and assuming Q can vary from 2 to 1:

16)	$\begin{array}{l}\displaystyle \gamma A_2 \overline{Y}_2 - \gamma A_1 \overline{Y}_1 + \gamma \left( \frac{A_1+A_2}{2} \right) LS_0 - \gamma \left( \frac{A_1+A_2}{2} \right) L\overline{S}_f = \frac{Q_1\gamma}{g} \beta_1V_1 - \frac{Q_2\gamma}{g} \beta_2V_2\end{array}$

17)	$\begin{array}{l}\displaystyle \frac{Q_2\beta_2V_2}{g} + A_2 \overline{Y}_2 + \left( \frac{A_1+A_2}{2} \right) LS_0 - \left( \frac{A_1+A_2}{2} \right) L\overline{S}_f = \frac{Q_1\beta_1V_1}{g} + A_1 \overline{Y}_1\end{array}$

18)	$\begin{array}{l}\displaystyle \frac{Q_2^2\beta_2}{gA_2} + A_2 \overline{Y}_2 + \left( \frac{A_1+A_2}{2} \right) LS_0 - \left( \frac{A_1+A_2}{2} \right) L\overline{S}_f = \frac{Q_1\beta_1}{gA_2} + A_1 \overline{Y}_1\end{array}$

(18) is the functional form of the momentum equation that is used in HEC-RAS. All applications of the momentum equation within HEC-RAS are derived from equation 2-37.