As concentration increases (Cv>60%), stress-strain relationship starts to depart from the linear, Bingham approximations. Non-Linear stress-strain relationships can be "dilatant" (stress rises faster than strain) or "pseudoplastic" (where strain increases faster than stress). Both mudflows and grain flows are dilatant. The Debris Library models both mudflows and grain flow stress as second order relationships with strain (\tau = f(\dot \gamma)^2)), making these models "quadratic-dilatant" (in the figure below).
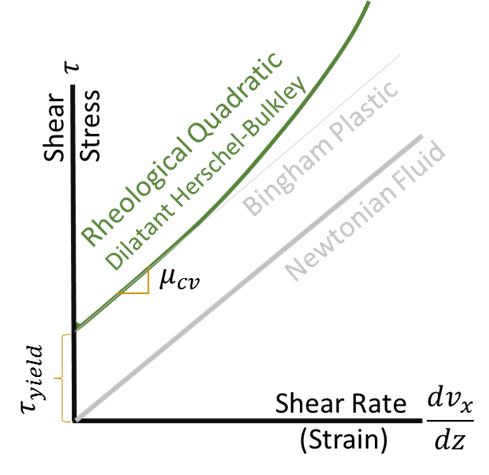Both mudflows and grain flows have volumetric concentrations greater than 60%. At these concentrations, particle interactions become important (though they are more important for coarser particles) but the fluid is still the dominant phase, transporting the solids. These high concentration flows are distinguished primarily by the grain size of the transported materials and the grain interactions during the transport process. Both used the second-order (quadratic), dilatant, rheological model (figure above), but they include different second order terms in this relationship.
Mudflows (or turbidity currents) transport high concentrations of fine grain material. The influences of grain-to-grain collisions are not as important with these finer materials. However, at very high concentrations (Cv>60%), inter-particle turbulence introduces non-linearity into the stress-strain relationship. So, in addition to the yield and (linear) viscous shears from the hyperconentrated flows, mudflows add a non-linear turbulent shear.
Grain flows occur at the same volumetric concentrations as mudflows (Cv>60%), but transport coarser sediment. Therefore, the stress-strain relationship has to account for particle collisions, in addition to the viscous and turbulent processes. Therefore, mudflows have the same quadratic rheological behavior as Mudflows (figure above) but add an additional second order term, a dispersive stress, to the turbulent stress used for mudflows.
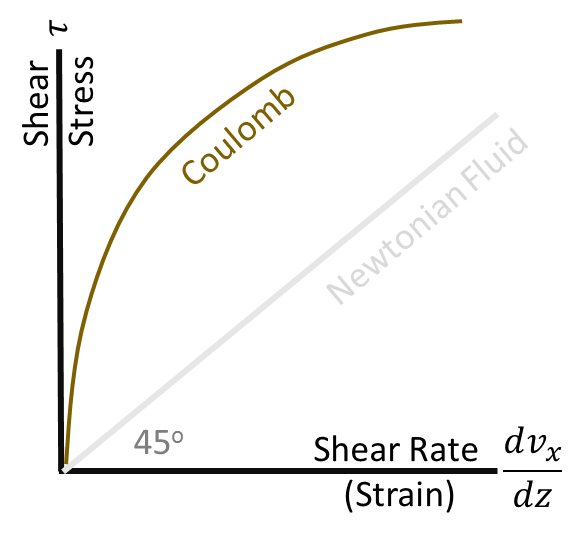
Debris flows have such high concentrations and, usually, large particles, that the particles are in persistent contact. The particles are no longer primarily suspended by the fluid and periodically collide. The coarse particle concentration is high enough that the fluid pushes the sediment and other large "debris" (e.g. trees and infrastructure) over other particles. Denlinger (2001) illustrates the main distinction between grain flows and debris flows in the figure below. Grain flow particles are still largely suspended, making them "collision dominated" (figure below, left) while debris flows particles mostly maintain contact with each other, making them "friction dominated" (figure below, right). Persistent, inter-particle friction dominates debris flow requires a geotechnical friction model. The Debris Library uses a Mohr-Coulomb model (bottom-most figure) to simulate these friction dominated processes.
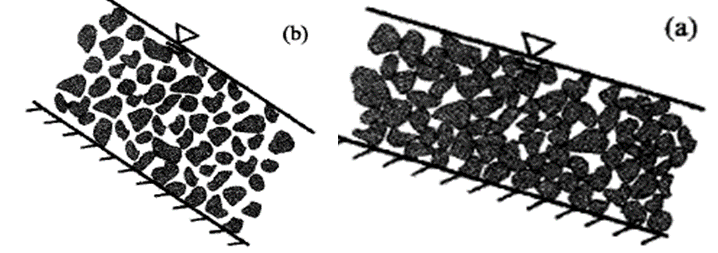
Landslides cap the upper end of the debris flow continuum. At low enough water contents and high enough volumetric solid concentrations, flow models are no longer appropriate. These events are gravity dominated, occur more rapidly, and require geotechnical failure models.