Sediment increases the viscosity of the flow mixture. There are many empirical and semi-empirical equations in literature to compute the viscosity of the mixture. HEC-RAS provides four ways of specifying the dynamic viscosity:
- User-specified constant
- User-specified ratio or relative viscosity
- Exponential
- Maron and Pierce (1956)
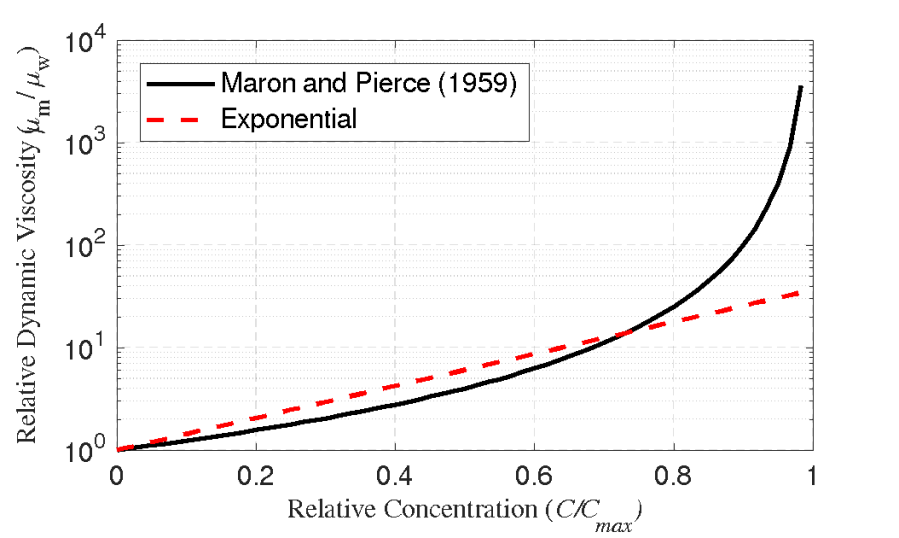
A comparison of the exponential (O'Brien et al., 1993) and Maron and Pierce (1956) formulas is shown in the figure below.
Ratio
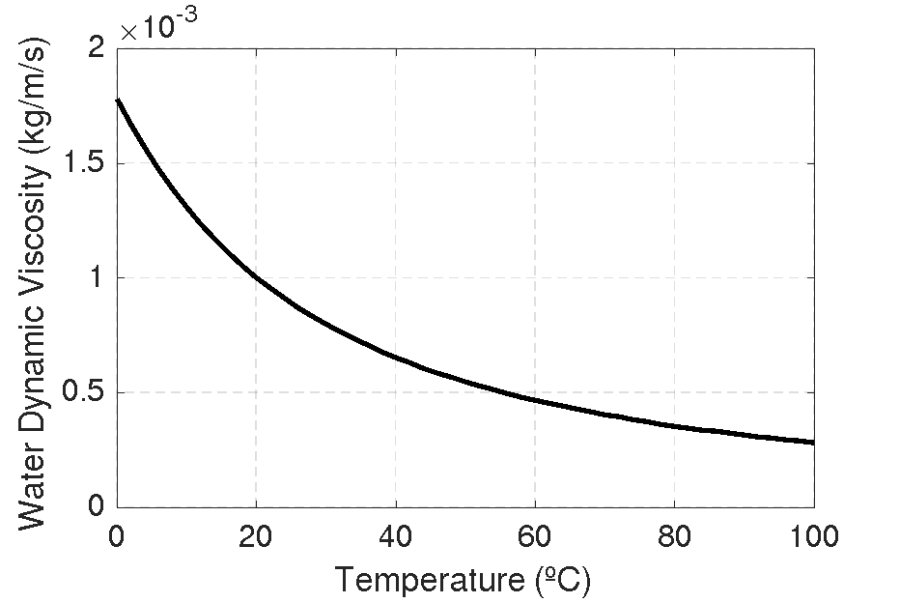
The ratio method in HEC-RAS basically specifies the relative dynamic viscosity. HEC-RAS computes the dynamic viscosity of the mixture as the water viscosity times the user-specified ratio. The water viscosity is computed internally based on the water temperature. The figure below shows the water dynamic viscosity as a function of temperature. Since the ratio is held constant and does not change with concentration or any other factors, the method is only recommended for simulations with constant concentration.
Exponential
A commonly used formulation for the mixture dynamic viscosity is the exponential expression (Chien and Ma, 1958; Dai et al., 1980; O'Brien and Julien, 1988). The formula is usually written as a two-parameter expression. However, here a simpler form is adopted to compute the relative dynamic viscosity as
|
\mu_r = \frac{ \mu_m } { \mu_w } = \exp (\beta C_v) |
where \mu_r is the relative mixture dynamic viscosity, \mu_w is the water dynamic viscosity, \mu_m is the mixture dynamic viscosity, C_v is again the volume concentration, and \beta is a coefficient fit to observed data and provided by the user. The advantage of the above formulation is that it only requires one empirical parameter and also satisfies the property \mu_r=1 for C_v= 0. In addition, by using the relative dynamic viscosity, the formula automatically takes into account the variation in water viscosity due to temperature. The variability in the coefficient \beta accounts for the effects of particle size distribution and, in particular, the cohesion of the sediment. One limitation of the formula however is that the viscosity tends to be underestimated as the concentration reaches the maximum concentration.
Table: Sediment laden viscosity parameters for the Exponential equation from O'Brien and Julien (1995).
Material | |
"Typical soil" | 8 |
Kaolinite | 8 |
Sensitive Clays | 5 |
Bentonite | 100 |
Maron and Pierce
Maron and Pierce (1956) proposed the following simple empirical expression for the relative dynamic viscosity
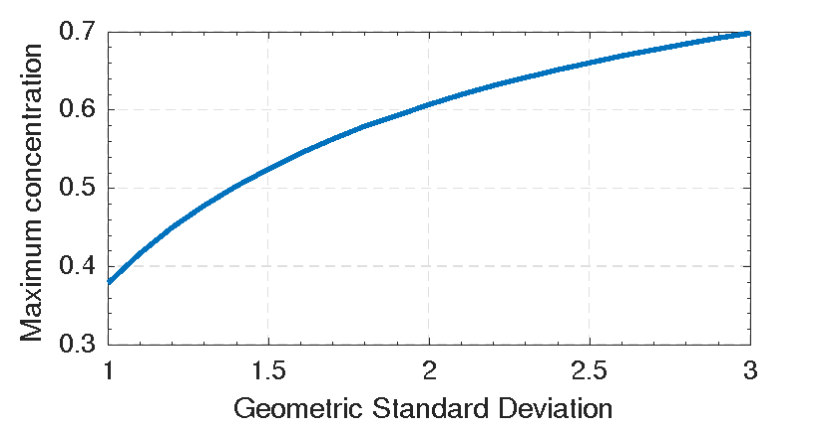
|
\mu_r = \frac{\mu_m}{\mu_w} = \left ( 1 - \frac{C_v}{C_{max}} \right )^{-2} |
where C_{max}is the maximum concentration by volume (maximum packing volume fraction). The maximum concentration is the concentration where enough particles have been added for the mixture to behave as a solid. Li (2004) and Guazzelli and Pouliquen (2018) compared various experimental datasets of viscosities of suspensions and found that the above formulation fits a wide range of experiments relatively well for a wide range of concentrations. Another advantage of the formulation has the advantage is that it does not require additional calibration parameters as does the O'Brien equation. The formulation is a function of the maximum concentration; however this variable is a physical property of mixture which can be more readily measures or estimated and does not have such a large range of values as does the β coefficient in the O'Brien formulation. The maximum concentration is a function of the sediment size distribution, particle deformability, and the local flow conditions. In practice however, an approximate maximum concentration may be estimated as Cmax=1-pm' in which pm' is the bed porosity. An example of the maximum concentration calculated from the proposed formula for bed porosity by Wooster et al. (2008) is shown in the Figure below. Natural sediments typically have porosities between 0.3 and 0.46.