Rheological Models

Rheology is the study of mechanical properties and flow of matter, specifically non-Newtonian fluids, mixtures, and plastic solids.

Bingham

The Bingham (Bingham 1922) model is one of the simplest of the rheological models. It Bingham stress is the sum of the yield and viscous stresses

$\begin{array}{l}\displaystyle \tau_{MD} = \tau_y + \tau_v\end{array}$

$\begin{array}{l}\displaystyle \tau_v = \mu_m \dot{ \gamma }\end{array}$

where $\begin{array}{l}\tau_y\end{array}$ is the yield stress, $\begin{array}{l}\tau_v\end{array}$ is the viscous stress, $\begin{array}{l}\mu_m\end{array}$ is the mixture dynamic viscosity, and $\begin{array}{l}\dot{ \gamma }\end{array}$ is the shear rate. This model has a linear stress-strain relationship, with a non-zero intercept. Therefore, $\begin{array}{l}\tau_y\end{array}$ and $\begin{array}{l}\tau_v\end{array}$ represent the intercept and the slope respectively of the stress-strain relationship. For stresses less than the yield stress the fluid behaves as a solid. The Bingham model is useful for simulating mudflows under low shear rates in which the yield and viscous stresses depend on the cohesion of fine sediments (Govier and Aziz, 1982; Julien 1995; Julien and Leon, 2000). However, the Bingham model has also been a practical model for use in simulating debris flows (Huang and Dai, 2014; Dai et al., 20)

Quadratic

The so called Quadratic model was proposed by O'Brien and Julien (1985) and combines stresses due to: (1) cohesion, (2) internal friction between sediment and fluid, (3) turbulence, and (4) inertial impact between particles. The quadratic model may be written as

$\begin{array}{l}\displaystyle \tau_{MD} = \tau_y + \tau_v + \tau_d \vspace{1} \tau_v = \mu_m \dot \gamma \vspace{1} \tau_d = c_{Bd} \rho_s \lambda^2 d^2_s \dot\gamma^2\end{array}$

where $\begin{array}{l}\tau_d\end{array}$ is the dispersive stress, $\begin{array}{l}c_{Bd}\end{array}$ is an empirical coefficient, $\begin{array}{l}\rho_s\end{array}$ is the sediment particle density, $\begin{array}{l}d_s\end{array}$ is a representative particle diameter, and $\begin{array}{l}\lambda\end{array}$ is the linear sediment concentration. The dispersive stress was originally proposed by Bagnold (1954). Bagnold (1954)and Takahashi (1980) proposed $\begin{array}{l}c_{Bd}\end{array}$ = 0.01. The linear sediment concentration $\begin{array}{l}\lambda\end{array}$ is defined by (Bagnold 1954)

$\begin{array}{l}\displaystyle \frac{1}{\lambda} = \left ( \frac{C_{max}}{C_v} \right )^{1/3} - 1\end{array}$

in which $\begin{array}{l}C_v\end{array}$ is the sediment concentration by volume and $\begin{array}{l}C_{max}\end{array}$ is the maximum sediment concentration. An example of the dispersive stress as a function of concentration and shear rate is shown in the figure below. The formulation shows a sharp increase as the concentration approaches the maximum concentration.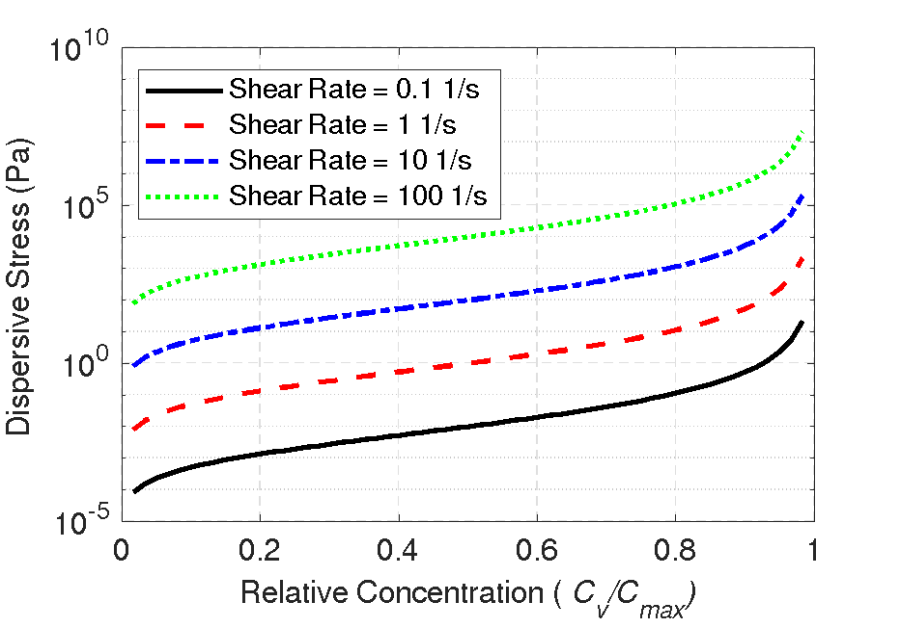

Herschel-Bulkley

In the Bingham rheological resistance model, the relationship between shear rate and shear stress is linear. However experiment have shown that debris-flow mixtures can have non-linear relationships (Major and Pierson 1992; Jeffrey et al. 2001). A more general model which allows for this nonlinearity is the Herschel-Bulkley (HB) model:

$\begin{array}{l}\displaystyle \tau_{MD} = \tau_y + \tau_{vd} \vspace{1} \tau_{vd} = K \dot {\gamma} ^n\end{array}$

where $\begin{array}{l}K\end{array}$ is the consistency factor or index, and $\begin{array}{l}n\end{array}$ is the power index or exponent. When $\begin{array}{l}n\end{array}$ < 1 the fluid/mixture is shear-thinning and when $\begin{array}{l}n\end{array}$ > 1 the fluid/mixture is shear thickening. The as with other rheological models, when the stress is less than the yield stress, the fluid/mixture behaves as a solid. One issue with the HB model is that the consistency factor as dimensional units which are a function of the power index. This makes estimating the parameter somewhat difficult. The HB model has been shown to work well for suspensions of fine sediments under high shear rates (Govier and Aziz, 1982).

Voellmy

The Voellmy resistance model combines a yield stress with a viscous/turbulent stress as (Voellmy 1955)

$\begin{array}{l}\displaystyle \tau_{MD} = \tau_y + \tau_{vd} \vspace{1} \tau_{vd} = \frac{ \rho_m g |\boldsymbol{V}|^2 } {\xi}\end{array}$

where $\begin{array}{l}\xi\end{array}$ is the Voellmy turbulence coefficient. Voellmy original proposed the formulation to simulate snow avalanches but it has since also been applied to simulate mud slides, debris flows, and rock avalanches (e.g. Hergarten and Robl, 2015; Hungr and Mcdougall, 2009; Körner, 1976; Perla et al., 1980; Rickenmann and Koch, 1997; Hussin et al., 2012). The Voellmy coefficient $\begin{array}{l}\xi\end{array}$ is similar to a Chezy coefficient and has units of L/T². Common ranges for the coefficient are from 150 to 600 m/s². In the Voellmy model, the yield stress is typically computed with the Mohr-Coulomb yield stress with the cohesion set to zero.