van Rijn_

van Rijn (1984) is a more recent method based on the flume and field data, and it has a good predictive ability in the dune and plane bed regimes. Van Rijn computes bed forms dimensions and the equivalent bed roughness. It estimates a Chezy-coefficient, which HEC-RAS converts into a Manning n, from bed roughness from flow, sediment transport parameters. The van Rijn method computes four key dimensionless parameters to estimate bed-form roughness.

1. Particle Parameter

   $$//<![CDATA[ \begin{array}{l}\displaystyle d_* = d_5_0 \left[ \frac {(s-1)g}{\nu^2} \right]^{1/3}\end{array} //]]>$$

   Where d50 is the median particle size (ft), s is the specific gravity ratio $//<![CDATA[ \begin{array}{l}(s = \frac{\rho_2}{\rho})\end{array} //]]>$, where ρs is the sediment density, and ρ is the fluid density, g is the gravitational acceleration and ν is kinematic velocity. 

2. Transport Stage Parameter: 

   $$//<![CDATA[ \begin{array}{l}\displaystyle T = \frac{(u'_s)^2-(u_{*,cr})^2}{(u_{*,cr})^2}\end{array} //]]>$$

   Which u*'is grain bed-shear velocity:

   $$//<![CDATA[ \begin{array}{l}\displaystyle u'_* = \frac{g^{0.5}}{C'}\=u\end{array} //]]>$$

   where u is mean flow velocity, C' is the Chezy-coefficient.

   $$//<![CDATA[ \begin{array}{l}\displaystyle C' = 18log \left(\frac {12R}{3d_{90}} \right)\end{array} //]]>$$

   where R is the hydraulic radius of the bed, u_*,cr is the critical Shields parameter

   $$//<![CDATA[ \begin{array}{l}\displaystyle u_{*,cr} = \sqrt{\frac{\tau_{cr}}{\rho}}\end{array} //]]>$$

   where τ_cr is the critical shear stress, and it is expressed as $//<![CDATA[ \begin{array}{l}\tau_{cr} = \tau^*_c \rho R g d_5_0\end{array} //]]>$, and the dimensionless critical shear is computed with the equation

   $$//<![CDATA[ \begin{array}{l}\displaystyle \tau^*_c = 0.5 \left[ 0.22Re_p^{-0.6} + 0.06 \times 10^{(-7.7 Re_p^{-0.6})} \right]\end{array} //]]>$$

   where

   $//<![CDATA[ \begin{array}{l}R = \frac {\rho_s - \rho} {\rho}\end{array} //]]>$, and $//<![CDATA[ \begin{array}{l}Re_p = \frac {\sqrt{gRD}D} {\nu}\end{array} //]]>$, and ρ is the fluid density. 

3. Bed-form dimensional parameters: The Bed-form parameter computes the bed form dimensions which the algorithm uses in the roughness computation:

   $$//<![CDATA[ \begin{array}{l}\displaystyle \frac{\Delta}{h} = 0.11 \left[ \frac{d_{50}}{h} \right]^{} \left[ 1-e^{{-0.5T}} \right] \left[25 - T\right] \vspace{1} \frac{\Delta}{\lambda} = 0.015 \left[ \frac{d_{50}}{h} \right]^{} \left[ 1-e^{{-0.5T}} \right] \left[25 - T\right]\end{array} //]]>$$

   and it computes a ratio of the bed form height to the wavelength: 

   $$//<![CDATA[ \begin{array}{l}\displaystyle \psi = \frac{\Delta}{\lambda}\end{array} //]]>$$

   Where ∆ is bed-form height, λ is bed-form length and is expressed as λ=7.3 h, and _h_ represents flow depth. If T≤0 and T≥25, bed would be considered almost plane, and C' calculated in step 2 will be used as Chezy-coefficient in step 4 for further calculation. ψ is bed-form steepness.

4. Equivalent roughness of bed forms: Finally, the algorithm uses the bed form height and height-to-wavelength ratio to compute a bed roughness.

   $$//<![CDATA[ \begin{array}{l}\displaystyle k_s = 3d_{90} + 1.1\Delta \left[ 1-e^{-25\psi} \right]\end{array} //]]>$$

   Van Rijn computes a Chezy-coefficient from the bed roughness:

   $$//<![CDATA[ \begin{array}{l}\displaystyle C = 18log \left( \frac {12R}{k_s} \right)\end{array} //]]>$$

   HEC-RAS converts the Chezy coefficient to a Manning's n (in English units) with the equation:

   $$//<![CDATA[ \begin{array}{l}\displaystyle n = 1.49 \frac {R^{1/6}} {C}\end{array} //]]>$$

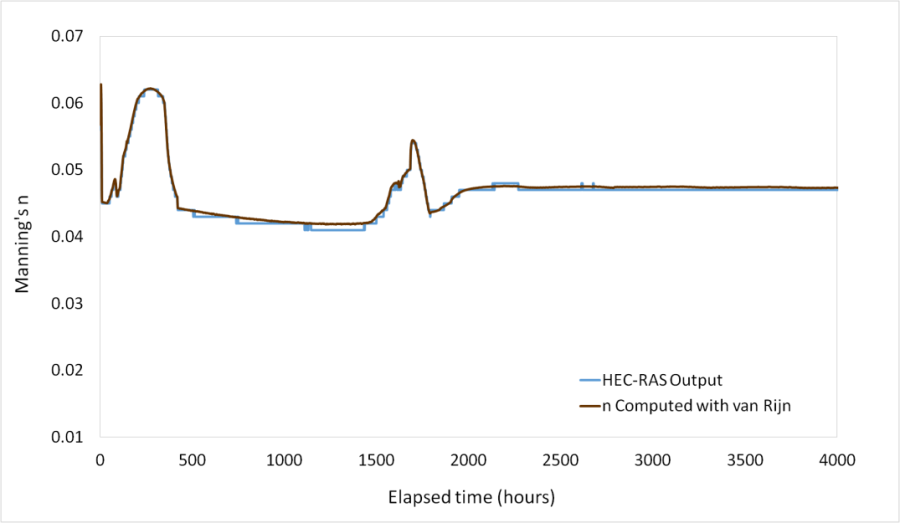
   An example roughness time series, using van Rijn (in HEC-RAS unsteady sediment transport) for a sand delta rapidly prograding into a gravel cross section, is included in the figure below.