Method of Slices

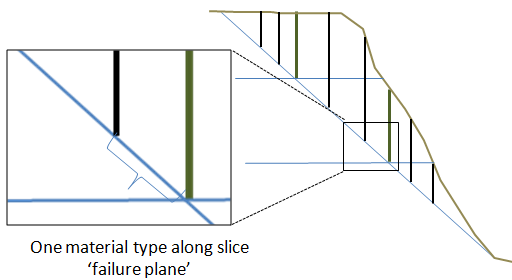
The Method of Slices methodology included in HEC-RAS follows the more classical geotechnical approach to planar failure. The formulation of the method of slices for bank failure analysis comes from Langendoen (2008). Before the analysis the algorithm divides each user specified material layer into three vertical slices of equivalent width (below). This ensures that the force and momentum balance computed for each segment of the failure plan will not include more than one material type.

Subdivision of layers into slices. The failure block through each layer is divided into three slices of equivalent width. The initial formulation of the method of slices (Bishop, 1955) considered forces acting at the base of each slice (along the failure plane) and included force (below) and momentum balances that were both vertical and normal to the slip surface. The Morgenstern and Price method (1965) added inter-slice forces in their analysis of earthen dams. The algorithms in USDA-ARS BSTEM for HEC-RAS include both inter-slice forces. The forces that act on each slice include: the weight of the slice W_j, the normal force acting on the base of the slice N_j, the shear force induced at the base of the slice S_j, inter slice normal forces E_j, and the vertical shear forces between slices X_j.
Forces acting on a slice
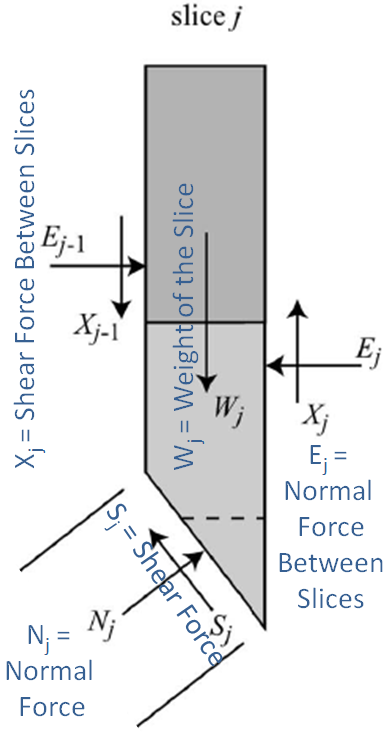
E_j and X_j= The inter-slice normal (E_j) and shear (X_j) forces are unique to the method of slices and deserve attention before the algorithm is described. Calculating inter-slice normal forces (E_j) from a horizontal force balance on the slice is relatively straight forward (Equation 4, Inter-slice Shear Forces). However, there is not an elegant theoretical approach to computing inter-slice shear forces. Stress-strain soil data demonstrate that there is a reasonably reliable empirical relationship of the ratio of inter-slice normal (E_j) and shear (X_j) such that:

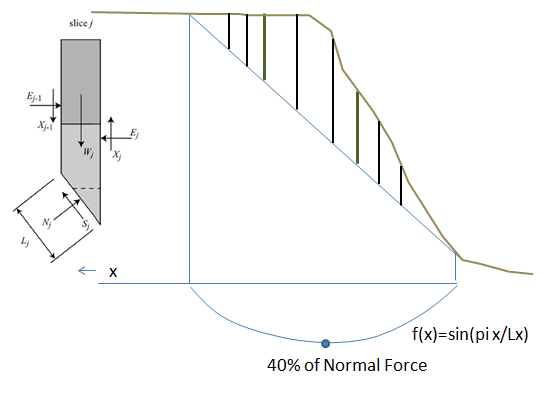
$\begin{array}{l}\displaystyle X_j = \lambda E_j f(x) = 0.4E_j sin \left( \pi x / L_x \right)\end{array}$

(4)
where:
λ =the maximum ratio (forty percent),
f(x)=a non-linear function between zero (0) and one (1) that apportions the ratio spatially,
x=the lateral distance into the bank
L=lateral width of the failure plane

In other words, at its maximum (in the center of the failure block) the shear force is forty percent of the normal force (below), and the shear-to-normal ratio decreases for slices farther from the center and closer to the margins.

Schematic of how the ratio of inter-slice shear stress to inter-slice normal ( equal to 0.4)stress is reduced by f(x) depending on the proximity of the slice to the center of the failure block.
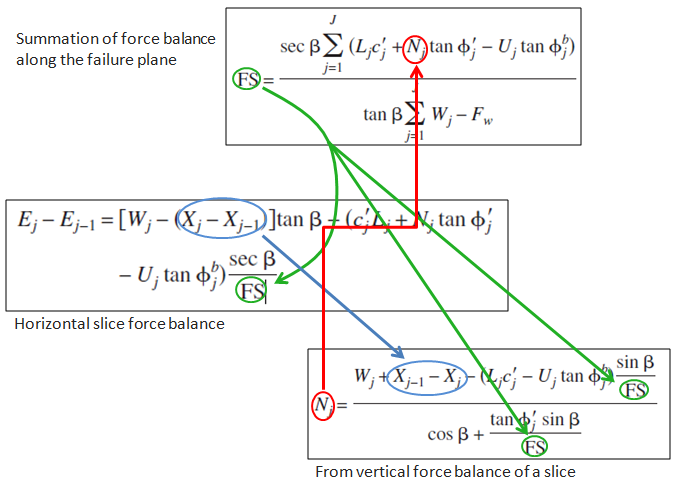
FS can be computed by summing (for all slices, j) the forces acting along the failure plane. The equation for computing FS along the failure slope is a familiar mix (from the Layer Method) of driving (red labels) and resisting (green labels), soil (brown circles) and hydraulic (blue circles) forces in the following equation (Force Balance).

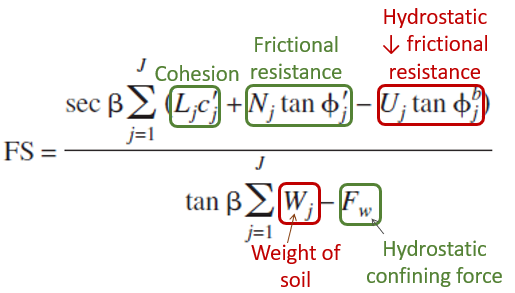force

where:

FS = factor of safety
U = hydrostatic uplift
P = hydrostatic confining force of the water in the channel
Φ' = friction angle
^Φb= relationship between matrix suction and apparent cohesion
c'= effective cohesion
W= weight of the soil
F_w= hydrostatic confining force

This is the Bishop (1955) approach that accounts only for the forces native to the individual slice. However, the normal force at the base of the slice is not a function of the forces intrinsic to the slice itself. It is modified by the inter-slice normal forces on either side (E_j and E_j-1) and the inter-slice shear (X_j and X_j-1) on either side of the slice. An iterative solution including two additional equations is required to compute these effects.
The inter-slice forces are calculated from the horizontal force balance (Equation 6, Horizontal Force Balance) for the slice:

$\begin{array}{l}\displaystyle E_j - E_{j-1} = \left[ W_j - \left( X_j - X_{j-1} \right) \right] tan{\beta} \ \left( c_jL_j + N_j tan{\phi_j^{'} - U_j tan{\phi^b_j} \right) \frac{sec{\beta}}{FS}\end{array}$

(6)
Equation 6 has FS imbedded and uses the FS computed in Equation 5. With FS being computed in Equation 5, and the shear forces between neighboring slices (X_j and X_j-1) coming from Equation 6, a Normal force at the base of the slice that is modified for inter-slice effects, can be computed from the vertical force balance (Equation 7) of the slice:

$\begin{array}{l}\displaystyle N_j = \frac {W_j + X_{j-1} - X_j - \left( L_jc_j^{'} - U_j tan{\phi^b_j} \right) \frac{sin\Beta}{FS}} {cos\beta + \frac{tan{\phi^{'}_j} sin\beta}{FS}}\end{array}$

(7)
The new normal force at the base of the slice is then substituted back into Equation 5 to compute a new FS, which is used to update the inter-slice forces in Equation 6 and to update the Normal force in Equation 7. The Method of Slices iterates on these three equations (below) until the change in FS between iterations drops below 0.5 percent.

There are some considerations in the code to decrease the computational expense of iteration. The code checks the denominators of the equations for FS and N_j to determine if iteration is necessary.

Iterative scheme to compute FS for the method of slices including the dependency of the normal force at the base of the slice on the inter-slice forces.