Laursen-Copeland

Laursen (1968) developed a total-load, excess-shear transport function with the form:

$\begin{array}{l}\displaystyle C = 0.01\gamma \left( \frac{d}{D} \right) ^{\frac76} \left( \frac{\tau^{'}}{\tau_c} - 1\right) f \left( \frac{u_s}{\omega} \right)\end{array}$

This equation makes Concentration (C) a function three dimensionless parameters, the ratio of the representative particle size (d) to the water depth (D), the rouse number (ratio of the shear velocity (u*) to the fall velocity (w) - and the dimensionless form of excess shear stress. Instead of making shear stress dimensionless with the Shields number, this equation makes the excess shear relationship dimensionless (similar to the dimensionless excess shear in the Partheniades equation):

$\begin{array}{l}\displaystyle \left( \frac {\tau ^{'}}{\tau_c} -1 \right) \space or \space \left( \frac {\tau^{'} - \tau_c}{\tau_c} \right)\end{array}$

Where t' is the grain shear stress and t_c is the critical shear stress. Laursen and Madden modified the transport function in 1963, to data from the Arkansas River. They updated the graphical function of the Rouse number based on additional data from the Arkansas River.

In the late 1980s, Ron CopelandCopeland, R. (1993) Numerical Modeling of Hydraulic Sorting and Armoring in Alluvial Rivers, Dissertation, University of Iowa, 284p (Appendix B). updated the equation again, including three significant developments. The Laursen-Copeland version of this function:

Expanded the empirical Rouse function f(u*/ω) to include additional data over a wide range of grain classes.
Replaced the total shear stress with a grain shear stress based on a hydraulic grain roughness.
Computed a dynamic, critical shear stress based on a variable Shields parameter.

Copeland's most significant update was the new empirical (fu*/ω) function. The Laursen transport approach builds the empiricism into this function which Laursen and Madden fit to a handful of available measurements in the 1960s. Copeland fit this empirical kernel to to flume results from seven gravel studies and two sand studies, and transport from six large sand or sand and gravel rivers (below). This expanded the applicable range of the transport function in both directions, including gravel and coarse silt, giving it the larges applicable range of the equations in HEC-RAS.
The Rouse number function from the three versions of the Laursen equation.
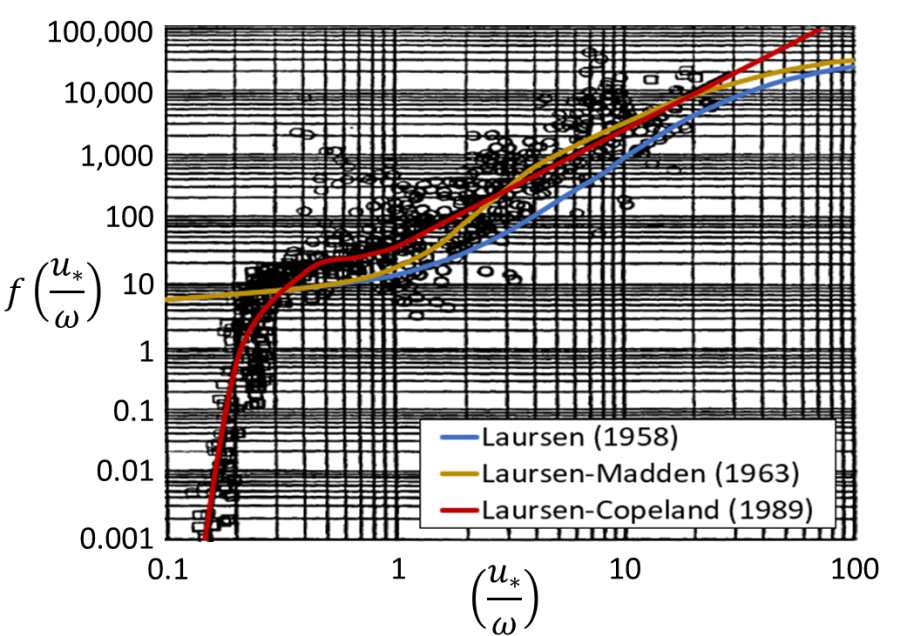
Second, Copeland exchanged total bed shear stress for grain shear stress by replacing depth (D) in Laursen's shear (τ') equation with the hydraulic radius due to grain roughness (R'), such that:

$\begin{array}{l}\displaystyle \tau^{'} = \frac{\rho V^2}{58} \left( \frac{d}{D} \right) ^{\frac13} \space becomes \space \tau^{'} = \frac{\rho V^2}{58} \left( \frac{d}{R^{'}} \right)^{\frac13}\end{array}$

where R' comes from the Limerinos equation (Burkham and Dawdy, 1976):

$\begin{array}{l}\displaystyle \frac{V}{u_s} = \frac{V}{\sqrt{gR^{'}S}} = 3.28+5.75log \left( \frac{R^{'}}{d_{84}} \right)\end{array}$

The hydraulic radius appears in both sides of this equation, so the transport function iterates to solve for R'.

Finally, the Laursen equation computes the dimensional critical shear stress from a stipulated dimensionless Critical Shields number (0.03). Copeland implemented Paintal's (1971) conclusion that the Shields parameter adjusts in response to the applied Shields stress. Therefore, the Laursen-Copeland equation adjusts the critical Shields parameter based on the dimensionless shear stress, such that:

The wide range of materials used to develop the Copleand version of Laursen's equation gives it the widest range of potential applicability of the transport functions included in HEC-RAS. It is the only transport function developed over the coarse silt range and unpublished work at Colorado State (Watson, personal communication) demonstrated that this equation outperformed other transport functions in the very fine sand and very coarse silt range.