Download PDF
Download page Step 4: Select the Appropriate Equations.
Step 4: Select the Appropriate Equations
It is very difficult to predict potential flood scour potential without historical measurements or a calibrated numerical model. However, it is important to consider scour failure modes even when data or calibrated models are not available. A suite of simple, empirical equations can bound the potential scour risk in these situations. These equations are not universally applicable and often generate a wide variety of scour depths. But applying the applicable equations - in an ensemble approach - can provide a possible range of scour depths. Many of these methods were collected in the US Bureau of Reclamation design manual (Pemberton and Lara, 1984) and despite their age and limitations remain the standard practice at the time of publication.
But it is critical to carefully select the equations that are appropriate for the design setting, or to weigh the results of each equation relative to their applicability.
The scour equations fall into two categories:
- General Scour
- Bend Scour
The first decision users must make is which suite of equations to consider. General scour equations tend to apply to straighter reaches and are often used to determine the depth of a pipeline or other infrastructure buried beneath a river crossing. Bend scour computes maximum local scour on the outside of the bend and is usually used to determine the depth of toe protection required to protect a bank or levee.
Bend scour estimates the multi-dimensional forces that scour the river bed on the outside of a bend. Bend scour equations are very sensitive to the "radius of curvature" of the bend. General Scour equations target straighter reaches, but most of these equations still have a categorical term that increases scour based on the curvature of the reach. These equations are based on 1D cross-section averaged variables and often – particularly the bend scour equations - refer to hydraulic parameters of an upstream, reference cross section. Equation variables that come from the upstream cross section have a subscript "US" below (e.g. DUS). Howard et al (2021) and Baird et al (2019) provide more detailed descriptions of the context and application of the equations summarized in this section.
These scour equations are included in a scour and RipRap calculator in the hydraulic modeling software HEC-RAS, which reads the hydraulic parameters directly from 1D model results and computes the applicable equations. For more information on the Scour equations and an example application, see Howard et al. (2021):
Howard, A., Pak, J., May, D., Gibson, S., Haring, C., Alberto, B., Snyder, M. (2021) "Approaches for Assessing Riverine Scour," Regional Sediment Management Technical Report.
General Scour
The general scour equations were compiled by Neill (1973) to compute scour at "constricted waterways." Pemberton and Lara (1984) present them as a method to "design buried pipe, buried canal siphon, or a bank line structure" and the complete suite are summarized in Baird (2019) and Howard et al. (2021). These equations estimate scour in different river settings, including bends or straighter reaches (Table 1) and are generally based on the hydraulic parameters at the design location (i.e. they do not refer to an upstream reference cross section).
Most of the General Scour equations (Neill Incised, Blench, Lacey, and USBR average velocity) have a similar form and using an empirical factor (Z) to account for sinuosity. Z is a categorical reduction factor with three options for "straight", "moderate", and "severe bends". The value of Z varies for the different equations based on the bend category collected. But the Z coefficient ranges from 0.25 to 0.75 for most natural river settings, reducing scour more (lower Z) for straighter reaches. Assigning a quantitative reduction factor to qualitative bend categories introduces uncertainty (and nonlinearity/step functions) into the analysis. But USACE Subject Matter Experts have some rule-of-thumb approaches to calculating these categories based on the ratio of the radius of curvature (Rc) and the bank-full channel width (W), summarized in Table 2.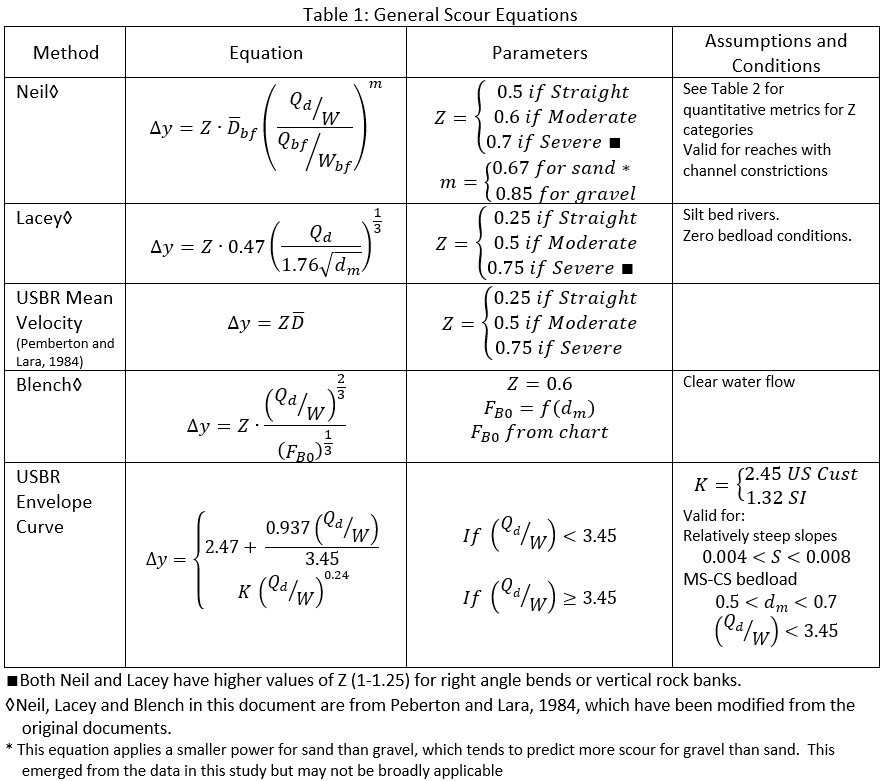
Where:
∆y is the scour depth below the initial channel invert
Qd is the design flow
dm median grain size
D is depth. Depth takes several forms in these equations including:
Dh, the hydraulic depth, which is the area divided by the top width
Dbf, the average bankfull cross section depth, but is often approximated with Dh and
D_Max, the maximum cross section depth.
Z is an empirical parameter accounting for channel sinuosity based on a categorical classification (See chart).
W is the flow width of the design event
Wbf is the banfull flow width
Qbf is the bankfull flow
FB0 is Blench's Zero Bed Factor from the figure below. 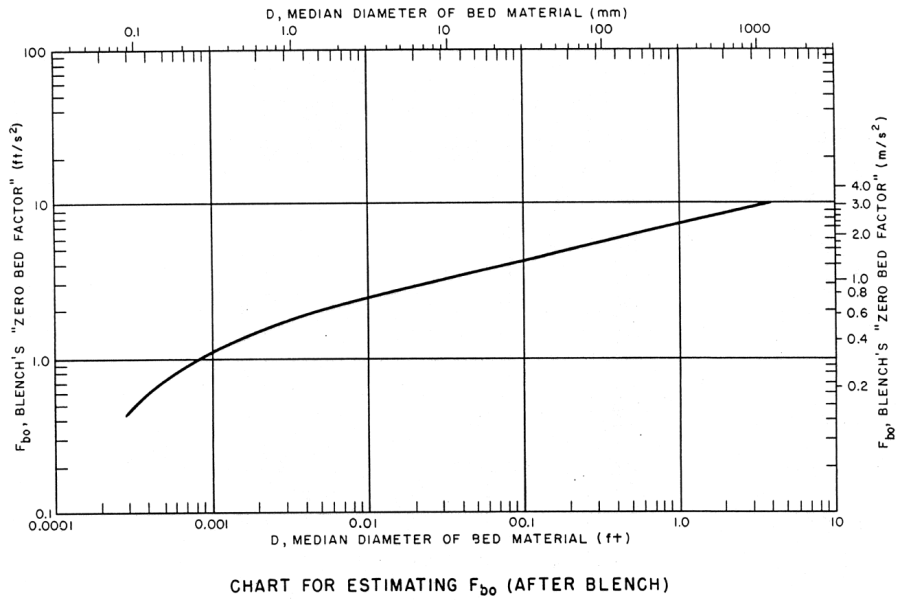
Chart to determine Blench's Zero Bed Factor as a function of dm (from Pemberton and Lara (1984) after Blench (1969)).
Radius of curvature to width ratios for curvature categories used to determine the Z factor.
Channel Description | R/W Range |
Severe | R/W<3 or 4 |
Moderate | 3 or 4<R/W<10 |
Straight | R/W>10 |
Pemberton form of Lacey Equation
Richards (2018) points out that the form of the Lacey equation in Pemberton and Lara (1984) - which is based on the total flow and is currently used in this calculator - is the regime form from the Lacey (1930) paper. Richards argues that the general version that uses unit flow is more appropriate in most situations. HEC and USACE are evaluating this finding. For now, the scour calculator uses the Bureau of Reclamation equation above, which is also applied by multiple other State and Federal agencies. But we are evaluating this equation and - for now- use this result with caution.
Bend Scour Equations
The bend scour equations try to account for multi-dimensional forces on the outside of a bend by quantifying the bend severity based on the bend curvature and computing constriction and avoiding the complexities of multi-dimensional hydraulics at the bend by tying the equations to an upstream "crossing" or "run" reference cross section (illustrated in the Figure below).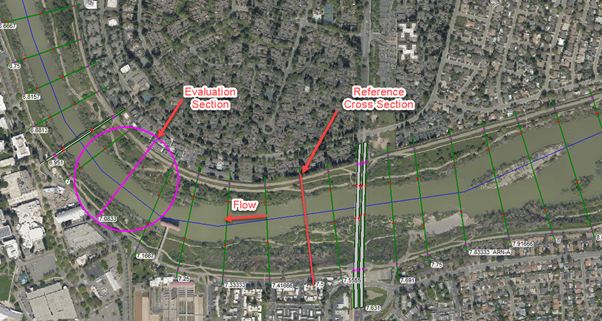
Most of these equations were based on flows at or below bankfull. Maynord 1996 (from Thorne) notes empirical methods are valid up until significant interaction between main-channel and overbank flow. Overbank depth should not exceed 20% of channel depth.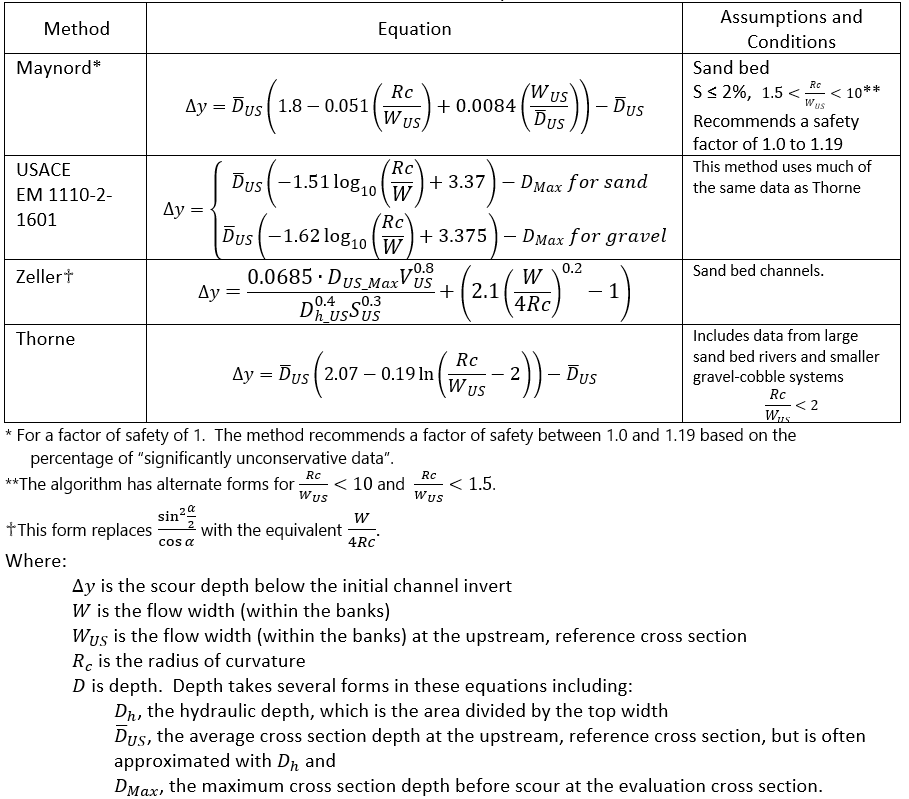
Warning and Error Messages
The Scour calculator will display a warning icon ![]() next to the computed value if it is problematic. Hover the cursor over the warning icon for a description of the error.
next to the computed value if it is problematic. Hover the cursor over the warning icon for a description of the error. Negative Scour:
Negative Scour:
In the current version, negative scour values will be the main reason for the warning icon. Because these equations are simple regressions of limited data sets, it is relatively common for them to report negative scour. But negative scour should never be included in a statistical analysis or interpreted as deposition. A negative scour is just a numerical artifact of a simple regression equation pushed outside its limits. Some practitioners and calculators report negative scour as 0, interpreting everything in the negative range as stable. In some cases, it may be appropriate to consider negative results part of a larger body of evidence that scour will be low. But the HEC-RAS scour calculator intentionally leaves these values negative to signal that the equation is outside the range of the equation and should be interpreted with care.
Outside the Equation Range:
Some equations will also show an error button if the calculator is applying the equation outside the stated range of the equation. The user can decide if the results are still valuable outside this range but should consider these warnings when selecting an applicable suite of equations.
In future versions HEC will add warnings for equations that are applied outside of their intended range. But for now, it is the user's responsibility to figure out which equations are site-appropriate.