Example 7. User Overrides (Low Outliers and Confidence Limits) – Rapid Creek above Canyon Lake near Rapid City, SD

Example 7 illustrates the computation of a peak flow frequency curve using EMA and Bulletin 17C procedures when a low outlier threshold and confidence limits are specified by the user. The data for this example comes from the USGS gage 06412500 Rapid Creek above Canyon Lake near Rapid City, South Dakota. Pactola Dam, which is located upstream of this stream gage, controls approximately 321 sq mi. As such, regulation effects were removed from the period of record. The annual maximum series for this example contains 90 peaks beginning in 1878 and ending in 2009. Information pertaining to 27 events not contained within the systematic record were sourced from a USGS report (Harden, O'Connor, Driscoll, & Stamm, 2011). Within this record, the June 1972 flood is by far the largest observed event. In fact, the June 1972 flood event is nearly 2.5 times larger than the next largest historical flood event and approximately 12 times larger than the next largest systematic (i.e. gaged) flood event at this location (Schwarz, Hughes, Hansen, Petersen, & Kelly, 1975). The annual maximum series is plotted in Figure 1 and tabulated in Table 1.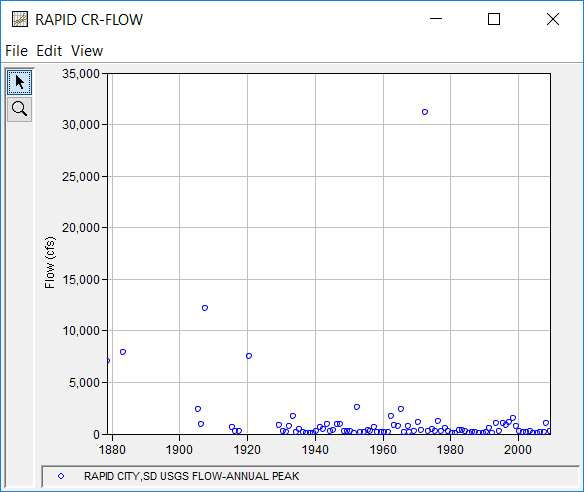


Table 1. Rapid Creek above Canyon Lake near Rapid City, SD Annual Peak Flow Record.

A Bulletin 17 Analysis using EMA and Bulletin 17C procedures has been developed for this example. To open the analysis, either double-click on the analysis labeled "B17C Example 7" from the Study Explorer or from the Analysis menu select open, then select "B17C Example 7" from the list of available analyses. When "B17C Example 7" is selected, the Bulletin 17 analysis editor will appear as shown in Figure 2. As shown, the Skew option was set to use the Station Skew and the default confidence limits were modified to 0.025 and 0.975 to produce a 95% confidence interval.

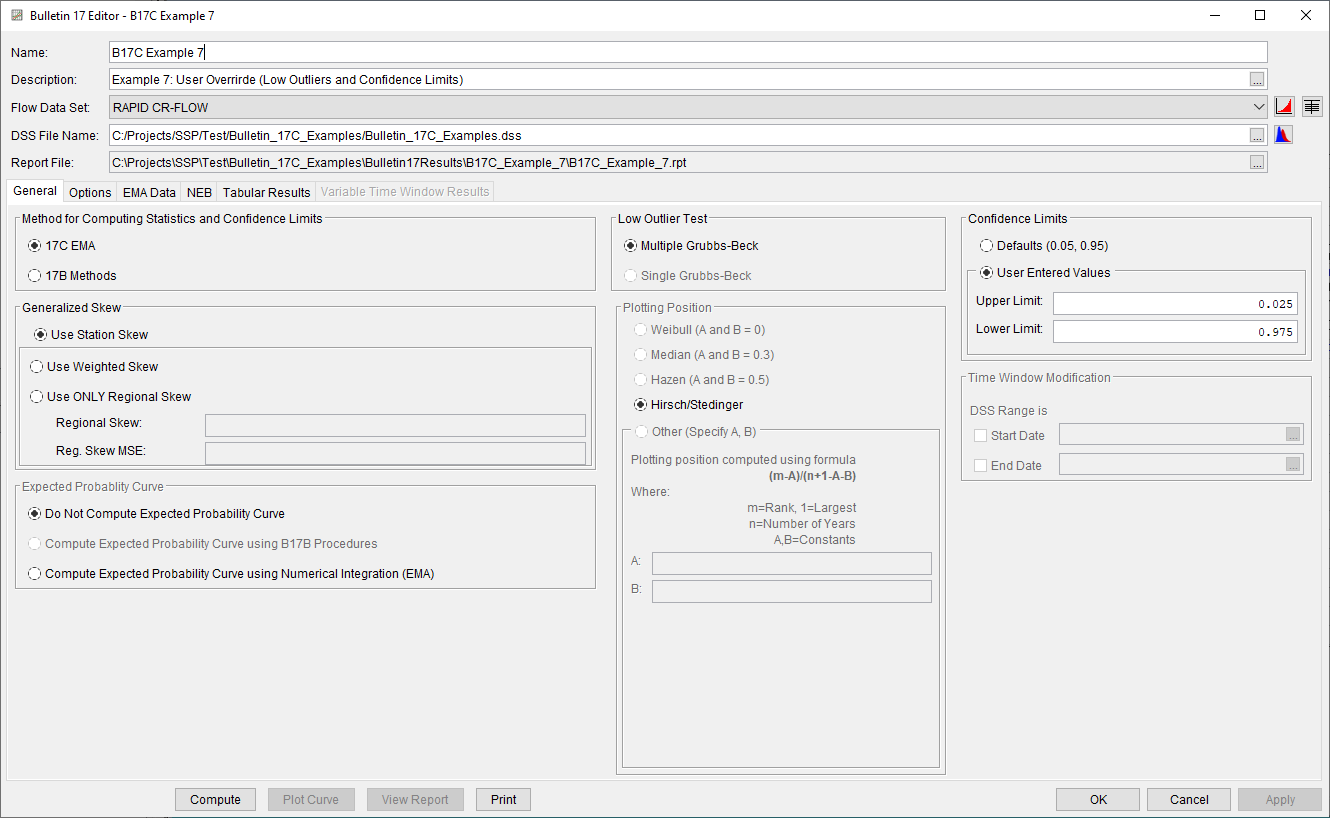
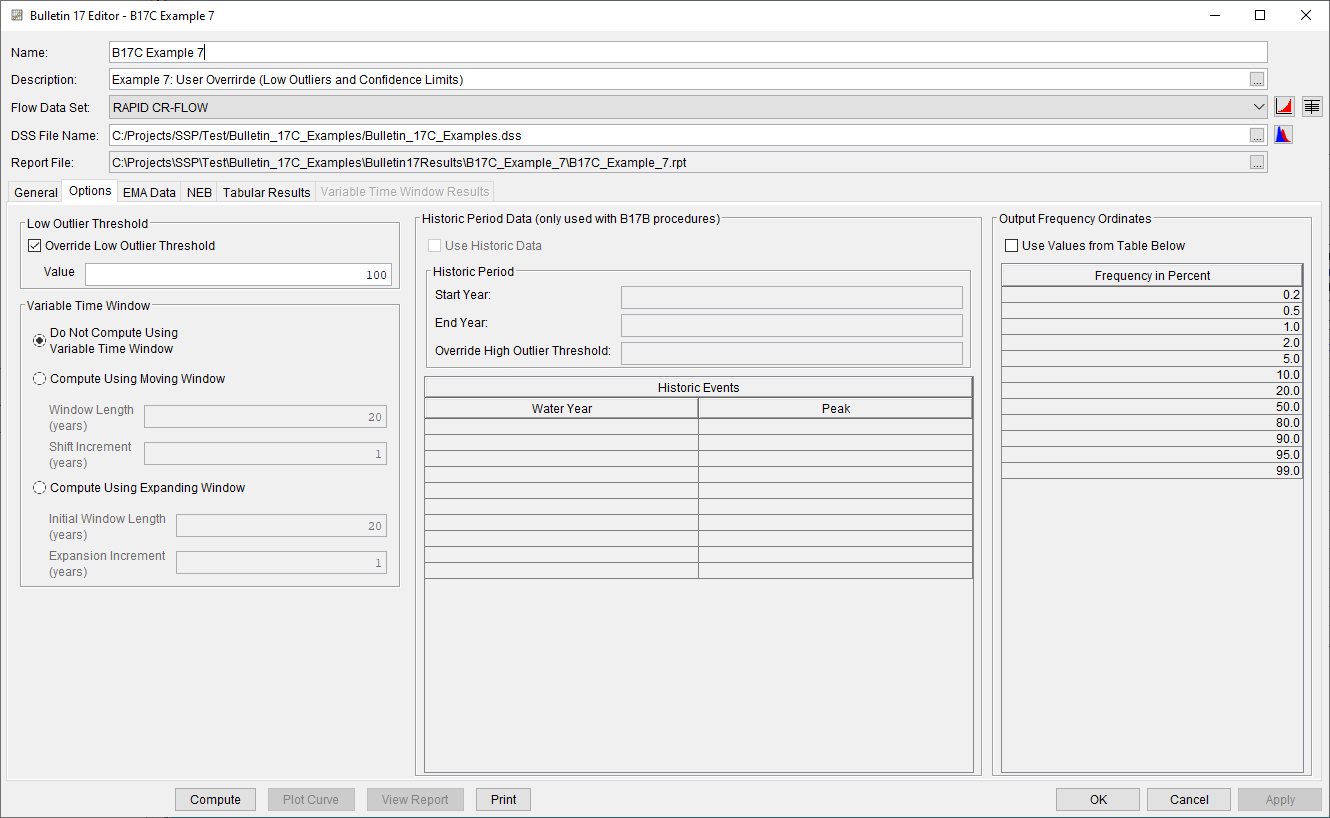
A low outlier threshold of 100 cfs was specified on the Options tab, as shown in Figure 3. This low outlier threshold was selected to censor more information than the default Grubbs-Beck critical value. When using this option, careful attention should be paid to the selection of the specified low outlier threshold as the resultant parameter estimation can be heavily impacted.

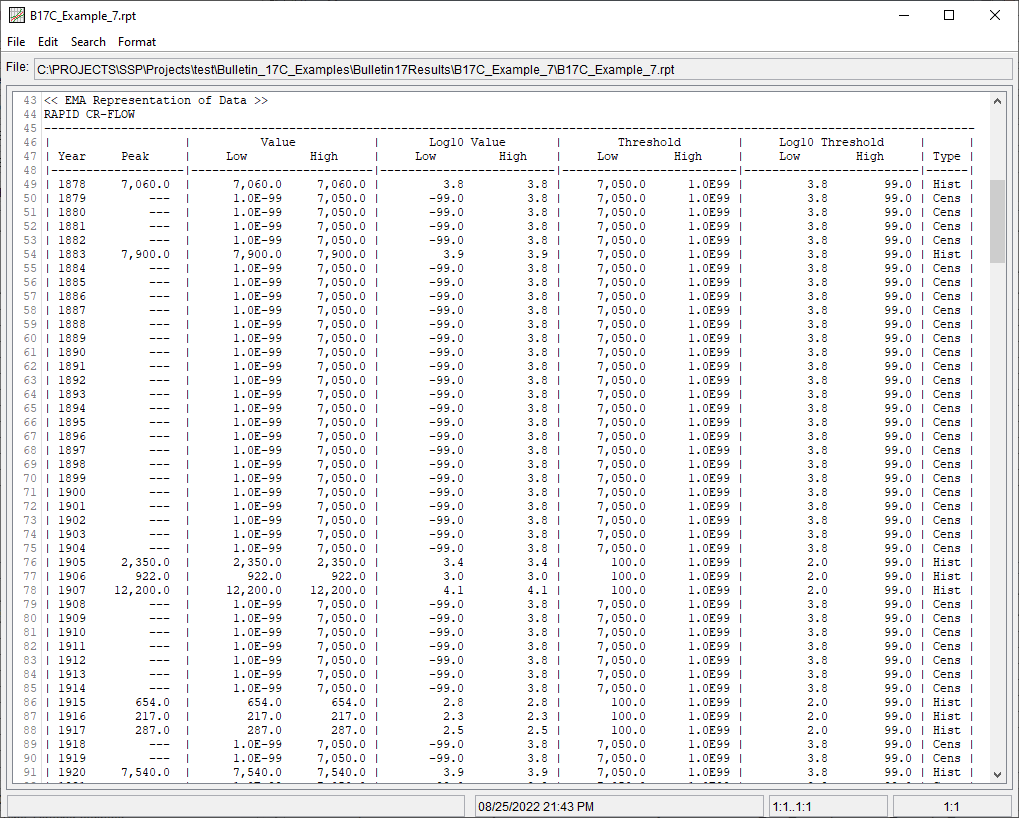
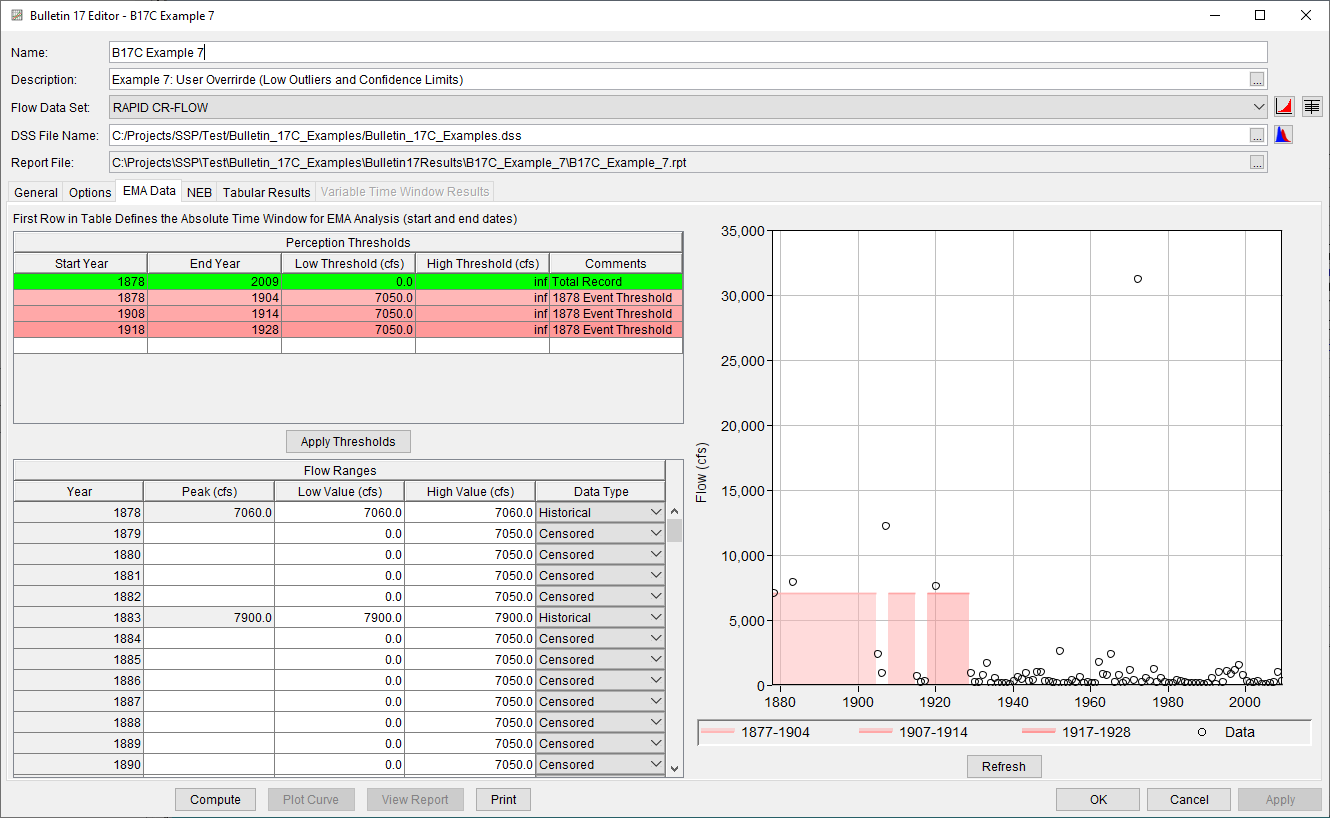
The EMA Data tab for this example is shown in Figure 4. This example uses an annual maximum series consisting of systematic and historical data with several missing periods. The missing periods span 1879 – 1882, 1884 – 1904, 1908 – 1914, 1918 – 1919, and 1921 – 1928. Since 17C EMA requires a non zero – inf perception threshold for all periods of missing data, a total of four perception thresholds are required. In this example, the June 1878 event can be used to inform the perception threshold for the missing periods of annual peak flow data. The use of a perception threshold of 7050 – inf for this period implies that had a flood event occurred with a peak flow greater than 7050 cfs, someone would have measured and recorded it. This value was chosen because historical events of this magnitude were in fact recorded. Once all four perception thresholds have been entered as shown in Figure 4, click the Apply Thresholds button to assign the complementary flow ranges for the periods of missing data.

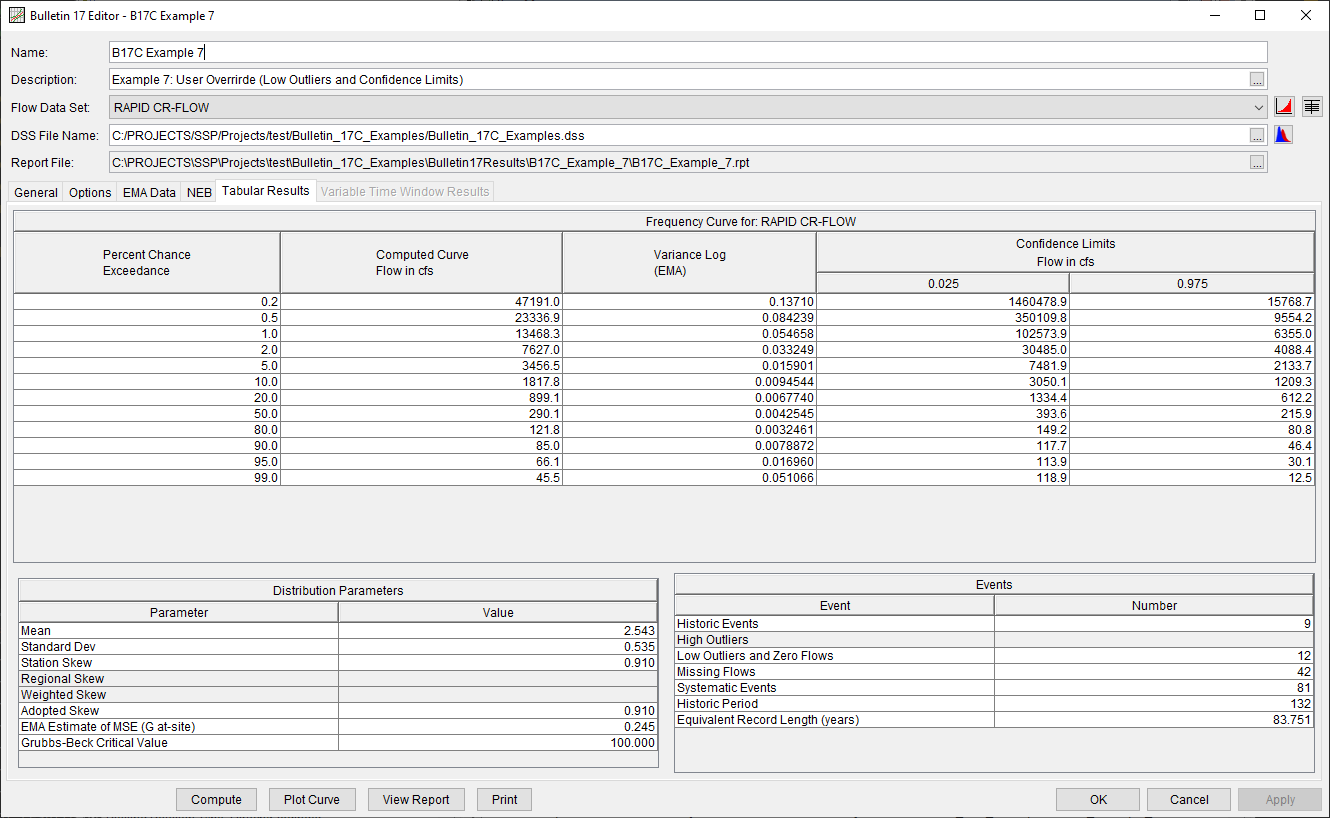
Once all of the General and EMA Data tab settings are set or selected, the user can press the Compute button to perform the analysis. Once the computations have been completed, a message window will open stating Compute Complete. Close this window and then select the Tabular Results tab. The analysis window should resemble Figure 5.

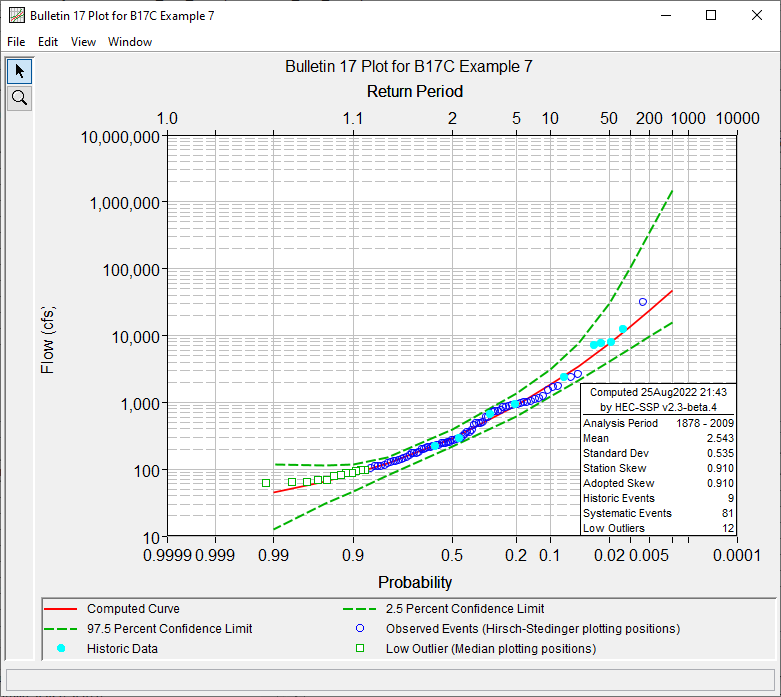
In addition to the tabular results, a graphical plot of the computed frequency curves can be obtained by pressing the Plot Curve button at the bottom of the analysis window. The Log Pearson Type III distribution fit using EMA to the input annual maximum flow data set, the 2.5% and 97.5% confidence limits, and the computed plotting positions are shown in Figure 6.

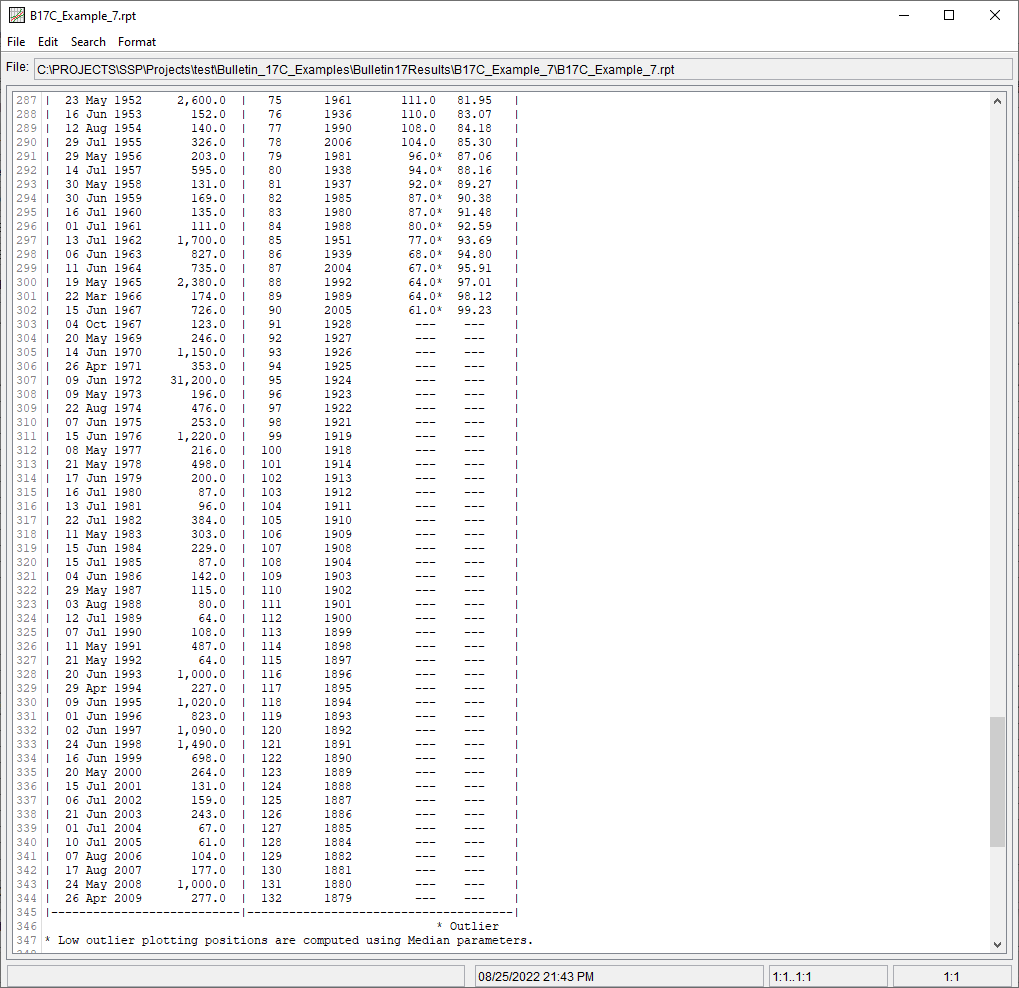
As shown in Figure 7, twelve values less than the defined low outlier threshold of 100 cfs were identified. These annual peak flows were then recoded to have a flow interval of zero – 100. The perception threshold for all systematic observations were also adjusted to correspond with the Multiple Grubbs-Beck Test low outlier threshold (i.e. 100 – inf), as shown in Figure 8.