Download PDF
Download page Peaks Over Threshold Frequently Asked Questions.
Peaks Over Threshold Frequently Asked Questions
When and why should I consider using a peaks over threshold model?
A peaks over threshold approach to frequency analysis should be considered when:
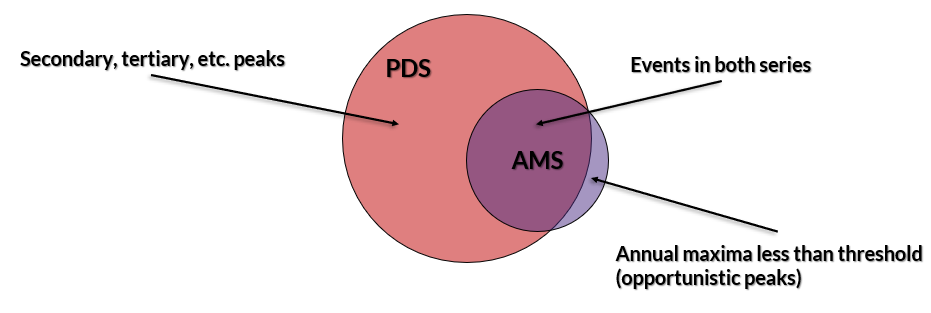
- The site experiences multiple flood events in some years.
- The annual maximum series contains events that aren't really extreme but happened to be the largest in a year ("opportunistic peaks") and/or low outliers.
- Sites where a suitable threshod corresponds to an average rate of > 1 event per year. An average rate exceeding 1 event per year means that the partial duration series (PDS) sample size is larger than the annual maximum series (AMS) sample size. A larger sample size has the potential to increase the predictive capability of the frequency curve.
- Sites that experience flood events caused by multiple flood-generating mechanisms (e.g. rainfall, rain-on-snow, and snowmelt), especially if the annual peaks are caused by different mechanisms. See the "How can a peaks over threshold model be used to model a mixed population?" question for additional information.
- The station skew computed using Bulletin 17C procedures is very negative (on the order of -0.5 or less). A very negative station skew could indicate that Bulletin 17C procedures are attempting to fit a distribution to a flood series that contains many small annual peak flow events.
The following plot shows a comparison of the AMS and PDS for Arroyo Seco at Pasadena, CA (11098000). The samples were extracted from 34 years (WY 1990-2024) of 15-minute streamflow data. Arroyo Seco is an ephemeral stream located in southern California. The Pasadena gage has a drainage area of 16 square miles and recorded a number of very low annual peak flows. Two of the largest six flow events (indicated by red arrows) are not included in the AMS because these events were secondary peaks.

The following table lists some of the advantages and disadvantages of block maxima and peaks over threshold modeling.
| Block Maxima | Peaks Over Threshold | |
|---|---|---|
| Advantages |
|
|
| Disadvantages |
|
|
Is a peaks over threshold model appropriate to use for hydrometeorological variables other than flow?
Yes. The peaks over threshold model is based on Extreme Value Theorem II, which states that the distribution of exceedances over a sufficiently high threshold will converge to the Generalized Pareto distribution. Hydrologists are often interested in extreme events and a peaks over threshold model can be used for frequency analyses of these variables. The Peaks Over Threshold Analysis in HEC-SSP can be used to perform a frequency analysis on many hydrometeorological variables (flow, precipitation, wind speed, etc.).
What does U.S. Army Corps of Engineers and U.S. federal guidance say about peaks over threshold modeling?
Engineer Manual (EM) 1110-2-1415 Hydrologic Frequency Analysis, published in 1993, provides guidance and procedures for frequency analysis of flood flows, low flows, precipitation, water surface elevation, and flood damage. In Chapter 2: Frequency Analysis, a discussion of annual maximum series and partial duration series is provided:
Annual Series Versus Partial Duration Series. There are two basic types of frequency curves used to estimate flood damage. A curve of annual maximum events is ordinarily used when the primary interest lies in the larger events or when the second largest event in any year is of little concern in the analysis. The partial-duration curve represents the frequency of all independent events of interest, regardless of whether two or more occurred in the same year. This type of curve is sometimes used in economic analysis, where there is considerable damage associated with the second largest and third largest floods that occurred in some of the years. Caution must be exercised in selecting events because they must be both hydrologically and economically independent. The selected series type should be established early in the study in coordination with the planner and/or economist. The time interval between flood events must be sufficient for recovery from the earlier flood. Otherwise damage from the later flood would not be as large as computed. When both the frequency curve of annual floods and the partial-duration curve are used, care must be exercised to assure that the two are consistent.
Selection of an appropriate threshold and ensuring independence between events in a partial duration series are discussed in later questions within this document.
EM 1110-2-1415 also describes the plotting positions of events in the partial duration series. When there are more events in the partial duration series than there are years in the record, the partial duration plotting positions provide the average number of exceedances of X in a year. The plotting positions computed from an annual maximum series provide the probability that the largest flood in a year will exceed the quantile.

Federal flood frequency guidance, Bulletin 17C, recommends partial duration series when minor floods, corresponding to annual exceedance probabilities greater than or equal to 1/10, are of interest. Bulletin 17C also states that analysts should follow the procedures detailed in the guidance "unless there are compelling technical reasons for departing from these Guidelines" and that "(n)o specific guidelines are recommended herein for conducting a partial-duration frequency analysis." Compelling technical reasons for using a peaks over threshold model in frequency analysis are described in the "When and why should I consider using a peaks over threshold model?" section.
How do I ensure that the events in my partial duration series are independent?
First, the threshold used to extract the partial duration series should be sufficiently high that the time series does not contain multiple values in a row above the threshold magnitude.
Time separation and/or magnitude differential criteria should be used to ensure that events in a partial duration series are independent. A time separation criterion means that a user-defined number of days must pass between events in order for them to be considered independent.
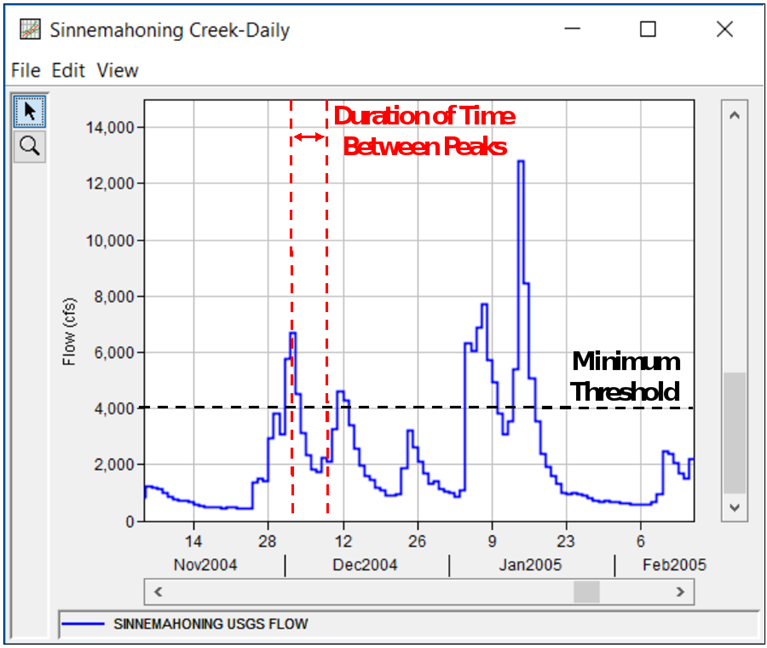
Application of agnitude differential criteria means that the variable must decrease by a user-defined magnitude or recede below a user-defined value between events. If the variable does not decrease by a user-defined amount, the time period is considered a single event. Three methods for computing magnitude differential are provided in HEC-SSP: Defined Threshold Value, Differential of Peak, and Percent of Peak. Users should investigate typical baseflow magnitudes (if flow is the variable of interest) to apply an appropriate magnitude differential criterion.



How do I select an appropriate threshold in a peaks over threshold analysis?
The threshold value differentiates between values that are considered extreme and those that are not. Selection of an appropriate threshold is critical for peaks over threshold modeling because the exceedances above the threshold converge to the Generalized Pareto distribution if the threshold is sufficiently high (Extreme Value Theorem II). If the threshold is too low, convergence does not occur. If the threshold is too high, the sample size of the partial duration series will be small.
For flows, bankfull discharge is a good a priori assumption since flows that stay within the river channel are not important in a flood frequency analysis. Methods for determining bankfull discharge are discussed in the next question. Bankfull discharge estimates in incised channels will be artificially high and should not be used as a starting point for determining a range of thresholds to investigate for a peaks over threshold analysis. For hydrometeorological variables other than flow (such as precipitation and wind speed), the minimum value in the annual maximum series or a value that produces an average rate of events of 1 can serve as starting estimates. Selecting a threshold that corresponds to an average rate of 1 event per year ensures that the partial duration series sample size and the annual maximum series sample size are equivalent. However, an average rate of 1 event per year does not have any special meaning beyond that and may correspond to a threshold value that is too low (or even too high). A weight of evidence approach should be used to select a threshold for peaks over threshold modeling.
HEC-SSP allows users to visualize diagnostic data for multiple threshold values to make an informed decision. For each threshold value (and other filtering criteria), HEC-SSP extracts the partial duration series and computes the following: (1) number of exceedances, (2) rate of exceedances, (3) Generalized Pareto distribution shape parameter, (4) mean excess, and (5) right-tail weighted Anderson Darling test statistic. The range of thresholds that are investigated can and should be refined iteratively. For example, a user could select a wide range of thresholds and then narrow the range as they get closer to an appropriate threshold value.
Five diagnostic data plots are produced in HEC-SSP: (1) number of exceedances, (2) rate of exceedances, (3) Generalized Pareto distribution shape parameter, (4) mean excess, and (5) Anderson Darling right tail weighted test statistic. Each of these quantities is plotted against threshold value.
The number of exceedances is the sample size of the partial duration series. For example, 50 exceedances of the threshold means that there are 50 events in the PDS.
The rate of exceedances is computed as the number of exceedances divided by the number of years of record. This is an average rate over the period of record.
The Generalized Pareto distribution is a three-parameter (location, scale, and shape) distribution. The shape parameter controls the tail behavior of the distribution. The smallest threshold value corresponding to a stable shape parameter is selected (Naghettini, 2017).
The mean excess plot shows the mean of the exceedances in the partial duration series. The threshold value corresponding to nonlinearity or a break in slope of the mean excess plot should be selected (Naghettini, 2017).
The right-tail weighted Anderson Darling test statistic is a goodness of fit test that assigns more weight to the upper tail of the distribution (Sinclair et al., 1990) and has been used as a threshold selection method in peaks over threhsold modeling (Solari et al., 2017). The Generalized Pareto shape and mean excess plots both evaluate the response of the shape parameter to the threshold value. The right-tail weighted Anderson Darling statistic evalutes the fit of the Generalized Pareto distribution to the partial duration series more holistically. In other words, the right-tail weighted Anderson Darling test statistic evaluates all three parameters (location, scale, and shape) because it quantifies the difference between the empirical distribution and the Generalized Pareto distribution.
The threshold value is the most important parameter in a peaks over threshold model. Selection of an appropriate threshold is an iterative process. The sensitivity of the results to the threshold value should be investigated.
How do I determine bankfull discharge?
Bankfull discharge is the flow rate that just fills the channel. Typically, flows that stay in bank are not of interest in flood frequency analysis wheras flows that exceed the channel capacity are considered floods.
Bankfull discharge is typically estimated from physical evidence. The following methods can be used to estimate bankfull discharge:
- Channel cross-section and Manning's equation
- A HEC-RAS model
- Inflection point(s) on a rating curve
- From sediment data (HEC-RAS Sediment Rating Curve Analysis Tool)
- Regional regression equations (e.g. Equations for estimating bankfull channel geometry and discharge for streams in Massachusetts)

How can a peaks over threshold model be used to model a mixed population (a flood series that is produced by multiple flood-generating mechanisms such as snowmelt, rain-on-snow, and rainfall)?
Using a peaks over threshold analysis, rather than a block maxima approach, to model a mixed population has advantages. The annual peak flows at a site might have been caused by multiple causal mechanisms, such as rainfall, rain-on-snow, and snowmelt. To develop independent and identically distributed ("IID") samples, the gage's annual maximum series should be divided by flood causal mechanism. However, dividing a gage's annual maximum series by flood type reduces an already small sample size. In addition, a site's annual peak flows might be dominated by one flood causal mechanism but secondary peaks, caused by another causal mechanism, could still be significant in magnitude. Since the block maxima approach considers only one flood per year, secondary peaks are omitted from the sample. An analyst could develop an annual maximum series for each flood causal mechanism (e.g. for a gage with 100 years of record, the analyst uses the 100 largest snowmelt floods and the 100 largest rainfall floods). However, this block maxima approach only works for flood causal mechanisms that produce a flood every year.
A peaks over threshold model allows for varying rate parameters to describe the average number of flood types per year (e.g. a gage has an average of 1 snowmelt flood per year, 0.75 rain-on-snow floods per year, and 1.5 rainfall floods per year over the period of record). A peaks over threshold model can also be used to model floods produced by meteorologic mechanisms that do not occur every year or do not produce significant flow events every year. One important exception is flood causal mechanisms that produce very small sample sizes (i.e. the flood causal mechanism only occurs in a small percentage of the years of record). Fitting an analytical distribution to a very small sample size is not appropriate.
When producing a flood frequency curve caused by multiple flood generating mechanisms:
- Use the same threshold value to develop a partial duration series for each flood generating mechanism. The threshold should be a physically-based value (i.e. corresponding to bankfull discharge) and should not vary based on the type of flood.
- Consider time separation criteria. For example, rainfall-driven hydrographs will recede more quickly than snowmelt-driven hydrographs. A time separation that ensures independence between events should be used.
- Once you develop a partial duration series for each flood type, compute an annualized frequency curve for each flood type.
- Use probability of union to compute the resultant frequency curve.
A single partial duration series was developed and used in the example below. The mixed frequency curve was obtained by treating all events in the PDS as identically distributed (i.e. disregarding flood causal mechanisms). Then, rainfall and snowmelt driven events were classified based on melting SWE in the days preceding each event. A Generalized Pareto distribution was fit to the rain events and to the snowmelt events. Finally, the combined frequency curve was computed from the rain and snowmelt curves using probability of union.

Which annualization method should I use and why?
Annualization refers to the conversion or adjustment of probabilities in partial duration space to probabilities in annual maximum space (i.e. annual exceedance probabilities, AEPs). When modeling exceedances above a threshold, the Generalized Pareto distribution is used. The Generalized Pareto distribution is the only analytical probability distribution that should be fit to a partial duration series. The Generalized Pareto distribution produces conditional probabilities, rather than AEPs. For analyses that require AEPs, such as flood risk management studies, annualization is a necessary step.
HEC-SSP provides users with two annualization methods. The first, the Langbein adjustment, is an empirical method (Langbein, 1949). The adjustment uses the average rate of events to convert the empirical partial duration probabilities to empirical AEPs. Since the Langbein adjustment is empirical, the procedure cannot extrapolate to probabilities beyond the observed values. As a result, the frequency curve cannot be extrapolated to frequencies more common than the threshold value or to frequencies that are rarer than the largest observed value.
The second annualization method available in HEC-SSP was developed by Madsen et al. (1997). This method converts the average rate of events and the Generalized Pareto distribution, computed from the partial duration series, to an equivalent Generalized Extreme Value (GEV) distribution. The GEV distribution is used to model the maximum of repeated samples of a homogeneous population (Extreme Value Theorem 1). Since the analytical annualization produces a fully parameterized GEV distribution, the frequency curve can be extrapolated to all probabilities. If quantiles beyond the range of observed values are required, analytical annualization should be used. Analytical annualization is the default annualization method in HEC-SSP.
I need to predict instantaneous/peak flow quantiles and want to use a peaks over threshold model. However, I don't have instantaneous data or my instantaneous flow record is short. What should I do?
Since off-the-shelf partial duration series are not readily available and instantaneous flow records tend to be short, analysts will likely use mean daily flow records for a peaks over threshold analysis. However, flood frequency analyses typically leverage instantaneous or peak flow data. As a result, conversion from mean daily to peak flow is needed.

There are many methods for converting mean daily flow values to instantaneous flow values. In addition, analysts can choose to apply the daily to instantaneous conversion to the sample values or to the computed quantile values. The relationship between mean daily and instantaneous flow values should be determined from observed flow events. Therefore, applying the adjustment to rare quantiles that are beyond the range of observed flow values is less defensible than applying the adjustment to the sample events.
Computing an instantaneous flow from mean daily flow is an area of active research. Two possible methods are: (1) linear regression and (2) quantile mapping.
More information on linear regression can be found in the Statistical Methods in Hydrology PROSPECT course material.

Quantile mapping adjusts the probability distribution of the modeled behavior (in this case, instantaneous values) such that it matches the probability distribution of the observed data (in this case, mean daily values). The quantile-quantile relation can be used to model parametric or non-parametric transformations and the distributions can be empirical or analytical.

Pairs of mean daily and instantaneous flows should correspond to the same event. For example, an instantaneous peak flow that occurred on 01 March 1938 should be paired with the mean daily discharge value that occurred on the same date. In addition, flow values should reflect unregulated conditions.
