Last Modified: 2023-07-14 11:28:10.031

Software Version

HEC-HMS version 4.11 was used to create this example. You can open the example project with HEC-HMS v4.11 or a newer version.

Project Files

Download the initial project files here:

SwampAngel_HMS_Start.zip

Introduction

The Energy Budget snowmelt method was introduced to HEC-HMS in version 4.11. Information on the Energy Budget method can be found in the HEC-HMS User's Manual and the HEC-HMS Technical Reference Manual.

The following parameters are required to use this method:

Rain Threshold Air Temperature
Snow Threshold Air Temperature
New Snow Albedo
Minimum Snow Albedo
Albedo Refresh Depth
Albedo Decay Coefficient Method
Albedo Decay Coefficient
Snow Thermal Conductivity
Liquid Water Retention Fraction
Snow Hydraulic Conductivity
Soil Depth for Energy Balance

In this tutorial, a parameter sensitivity analysis will be performed using the Uncertainy Analysis compute option in HEC-HMS and a regression analysis in Microsoft Excel. In evaluating parameter sensitivity, we are trying to answer the following questions:

Which parameters play the largest role in the outputs of interest?
Which parameter should be investigated (and uncertainty reduced) in future efforts?

Study Area

The Swamp Angel Study Plot (SASP) is located in the San Juan Mountains in southwestern Colorado. SASP is located at an elevation of 11,060 ft (3,370 m) and is located in meadow sheltered by the surrouding terrain and subalpine forest. The location of SASP allows for snowpack and precipitation measurements under minimal wind influence. SASP was used in the Earth System Model-Snow Model Intercomparison Project (ESM-SnowMIP). ESM SnowMIP is an international modeling effort that evaluates snow modeling schemes (Krinner et al. 2018).

For this tutorial, the study plot is treated as a point location. A simple HEC-HMS model with a single subbasin element was developed. The study plot has an area of 0.22 acres (0.0009 square kilometers).

Location of Swamp Angel Study Plot

Finish Model Set-up

Create a Meteorologic Model

Before performing a parameter sensitivity analysis, a meteorologic model must be created. Boundary conditions that are required to use the Energy Budget snowmelt method include:

Shortwave Radiation
Longwave Radiation
Precipitation
Air Temperature
Wind Speed
Atmospheric Pressure
Relative Humidity

Meteorological data used in this tutorial was obtained from the ESM SnowMIP data repository. Metric units are used in this tutorial to be consistent with the meteorological data.

Download the SwampAngel_HMS_Start project and unzip the file.
Start HEC-HMS (version 4.11 or newer) and open the SwampAngel project.
Expand the Basin Model folder in the Watershed Explorer and select the SwampAngel basin model. Notice that the basin model contains a single subbasin named SWA.
Create a Meteorologic Model by selecting Components | Meteorologic Model Manager. Click the New... button. Name the meteorologic model InSitu and click the Create button.
Close the Meteorologic Model Manager window.
Expand the Meteorologic Model folder in the Watershed Explorer and select the InSitu meteorologic model.
From the Component Editor, select the following:
- Unit System: Metric
- Shortwave: Specified Pyranograph
- Longwave: Specified Pyrgeograph
- Precipitation: Specified Hyetograph
- Temperature: Specified Thermograph
- Windspeed: Specified Anemograph
- Pressure: Specified Barograph
- Dew Point: Specified Humidograph
- Evapotranspiration: --None--
- Replace Missing: Set To Default
  
  The Meteorologic Model component editor should appear as in the figure below.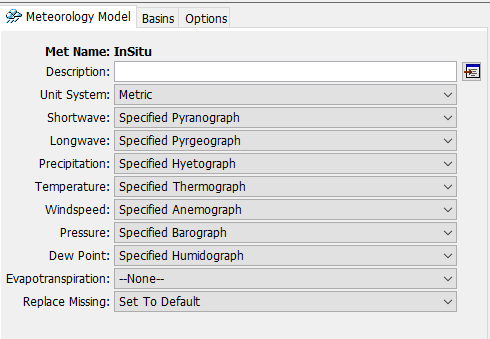
Within the Meteorologic Model Component Editor, navigate to the Basins tab. Under the Include Subbasins header, select Yes from the drop-down menu to link the SwampAngel basin model to the InSitu meteorologic model.
Select the Specified Pyranograph from the Watershed Explorer. Under the Gage header, select InSitu-Shortwave from the drop-down menu.
Repeat the previous step and make the following selections:
- Specified Pyrgeograph: InSitu-Longwave
- Specified Hyetograph: InSitu
- Specified Thermograph: InSitu
  - Lapse Method: --None--
- Specified Anemograph: InSitu
- Specified Barograph: InSitu
- Specified Humidograph: InSitu_humidity
Save the project.

Create and Compute a Simulation Run

Create a Simulation Run by selecting Compute | Create Compute | Simulation Run.... Name the run WY2006 and select the Next button. Select the SwampAngel basin model, the InSitu meteorologic model, and the WY2006 control specifications on the following screens. Select the Finish button.
Select the WY2006 simulation from the Compute Selection Box in the Toolbar.
Click the Compute button to run the simulation.
Navigate to the Results tab and expand the Simulation Runs folder.
Select the WY2006 simulation and expand the SWA subbasin.
Hold the keyboard Ctrl button and select the Observed SWE and Snow Water Equivalent output variables, as shown in the figure below.
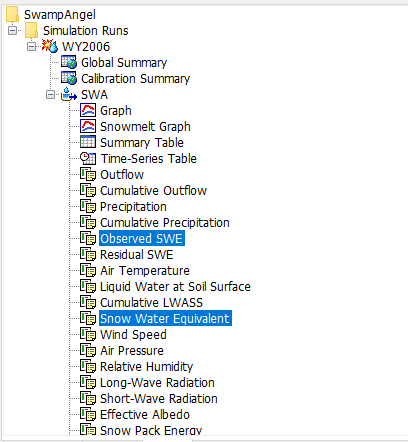
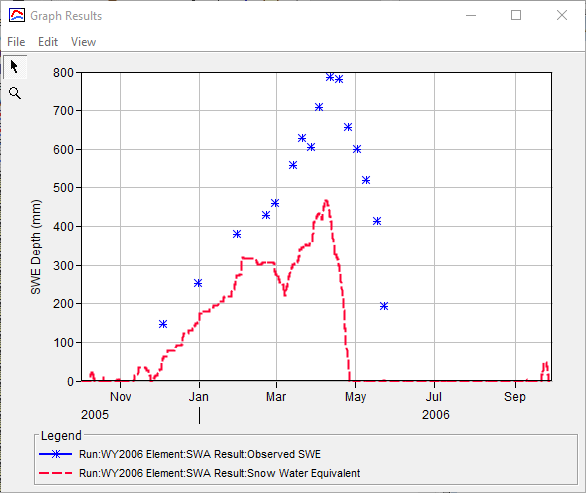
Select the Plot button from the Toolbar. The results should appear similar to the below.

You can edit the linestyle (e.g. color, symbol, etc) of a time series by clicking Edit | Plot Properties.

Create and Compute an Uncertainty Analysis

Create an Uncertainty Analysis by selecting Compute | Create Compute | Uncertainty Analysis....
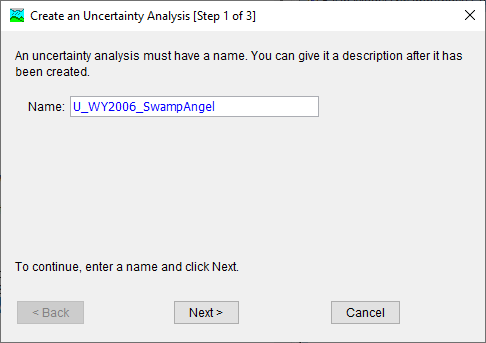
Name the Uncertainty Analysis U_WY2006_SwampAngel as shown in the figure below. Click the Next> button.
Select the SwampAngel basin model. Click the Next> button.
Select the InSitu meteorologic model. Click the Finish button.
Navigate to the Compute tab. A few folder titled Uncertainty Analyses was created. Expand the folder and select the U_WY2006_SwampAngel analysis.
In the Component Editor, select the gear icon next to the Analysis Points field. Click the checkbox next to the Snow Water Equivalent time series as shown in the figure below.
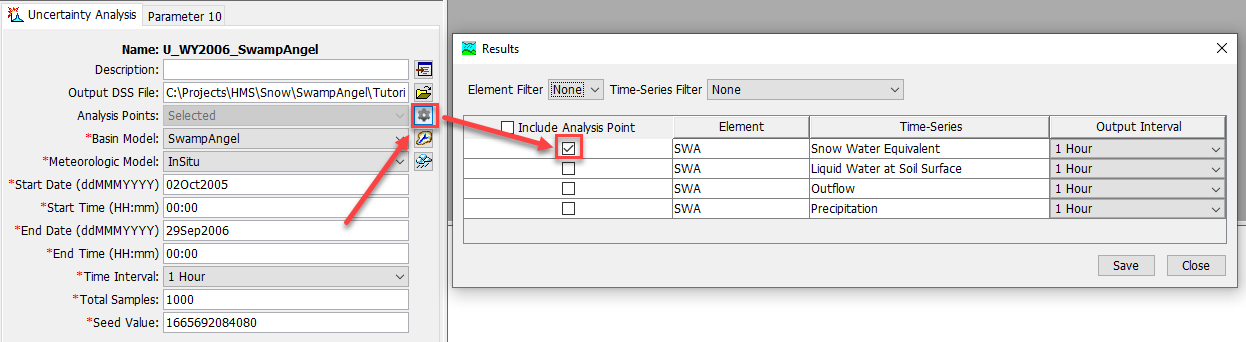
Click the Save and Close buttons.
In the Component Editor, enter the following for the Start Date/Time and End Date/Time:
- Start Date: 02Oct2005
- Start Time: 0000
- End Date: 29Sep2006
- End Time: 0000
Select a Time Interval of 1 Hour from the drop-down menu.
Enter 1000 in the Total Samples field. The Total Samples refers to the number of times the program will sample new parameter values and run a simulation.
Right click on the uncertainty analysis and select Add Parameter.
Repeat the above step 9 more times to add a total of 10 parameters.
For each parameter, select subbasin SWA in the Element drop-down menu.
On the Parameter tab, select Simple Distribution from the Method drop-down menu and Uniform from the Distribution drop-down menu. The uniform distribution was used for this parameter sensitivity analysis because no information about parameter distributions was available.

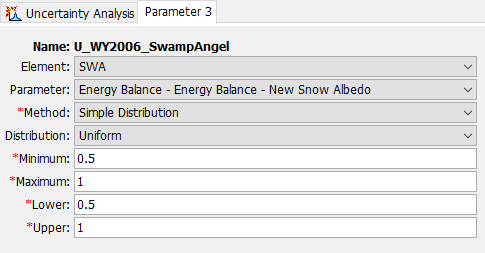
Enter the Minimum and Maximum for each parameter using the values in the table below. For the uniform distribution, the Minimum and Lower values are the same and the Maximum and Upper values are the same. Do not enter the units in HEC-HMS; they are provided for clarity. The Parameter tab for New Snow Albedo is shown in the figure below.

Parameter	Distribution	Minimum	Maximum	Units
Rain Threshold Temperature	Uniform	-3	3	deg C
Snow Threshold Temperature	Uniform	-3	3	deg C
New Snow Albedo	Uniform	0.5	1	-
Minimum Snow Albedo	Uniform	0.1	0.5	-
Albedo Refresh Depth	Uniform	0.01	10	mm
Albedo Decay Coefficient	Uniform	10	600	hr
Snow Thermal Conductivity	Uniform	100	1100	J/m/deg C/hr
Snow Capillary Retention	Uniform	0.001	0.25	-
Snow Hydraulic Conductivity	Uniform	0.0001	0.1	m/s
Effective Thermal Ground Depth	Uniform	0.001	0.5	m

Uncertainty Analysis parameter component editor

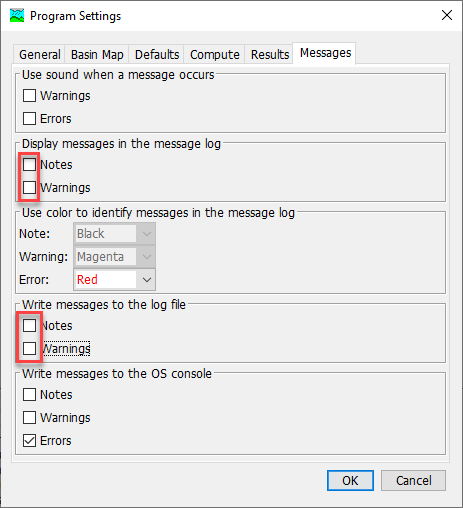
Turn off notes and warnings in the Message Log by selecting Tools | Program Settings.... Navigate to the Messages tab. Under the Display messages in the message log and Write messages to the log file sections, uncheck the boxes next to Notes and Warnings, as shown in the figure below. Displaying and saving messages increases the run time of the Uncertainty Analysis.
Compute the Uncertainty Analysis.

The simulation will take approximately 35 minutes to compute.

Extract Sampled Parameter Values

Navigate to the Results tab. Expand the Uncertainty Analyses folder and select the U_WY2006_SwampAngel uncertainty analysis. The Results tab should resemble the figure below.
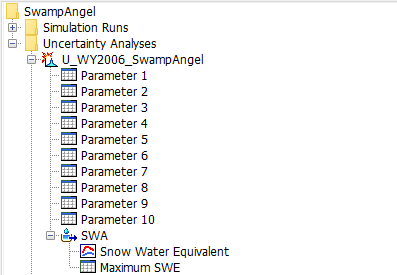
HEC-HMS provides the sampled parameter values for each realization. In addition, the SWE time series and maximum SWE value for each realization are provided. Select a Parameter node to view the sampled parameter values, as in the figure below.
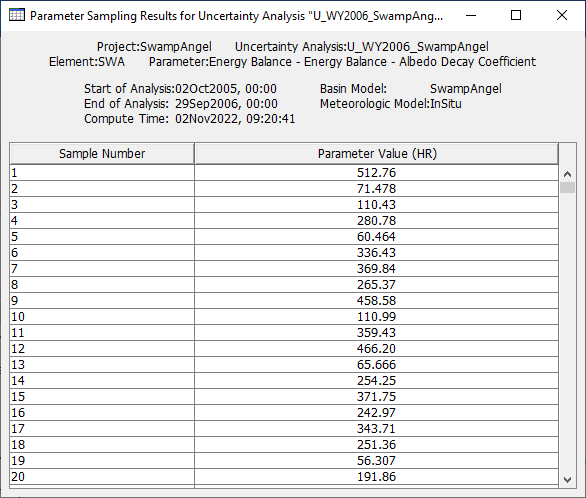
Open each Parameter node and copy the sampled parameter values to an Excel spreadsheet. Include a data label for each parameter (e.g. "Albedo Decay Coefficient").
Expand the SWA subbasin node and select the Maximum SWE time series node. Copy the output to Excel. Include a data label for the maximum SWE output.

Perform a Multiple Linear Regression Analysis in Excel

The parameter values are generated through random sampling. Your parameter values will be different from the values shown in this section unless the same Seed Value is used in the HEC-HMS Uncertainty Analysis. The Seed Value is used to itialize the random number generator. In general, it is not advisable to change the Seed Value unless you are trying to duplicate results.

Compute the mean and standard deviation of each parameter and the maximum SWE using Excel functions AVERAGE and STDEV.S. The Excel spreadsheet should look similar to the figure below.
Before performing a regression analysis, the sampled parameters and maximum SWE output must be standardized. The 10 parameters have different units and scales. Standardization is needed so that parameters with larger standard deviations do not have greater influence on the regression results. In addition, standardization ensures that the regression coefficients have uniform units. The parameters and output were standardized by subtracting the mean and dividing by the standard deviation:

$\begin{array}{l}Z_i = \frac{X_i - \bar{X}}{\hat{\sigma}}\end{array}$
The mean and standard deviation for each standardized variable should be 0 and 1, respectively. The results of the standardization should look similar to the figure below.
Multiple linear regression can be performed in Excel using the Analysis ToolPak. Select File | Options. Navigate to the Add-ins tab on the left side of the Excel Options dialog box. On the bottom of the dialog box, select Excel Add-ins from the Manage drop-down menu and click the Go... button. Select the check box next to the Analysis Toolpack add-in, as in the figure below. Click the OK button to close the dialog box.
Navigate to the Data tab | Analyze section | Data Analysis option.
Select Regression in the Data Analysis dialog box. Click the OK button.
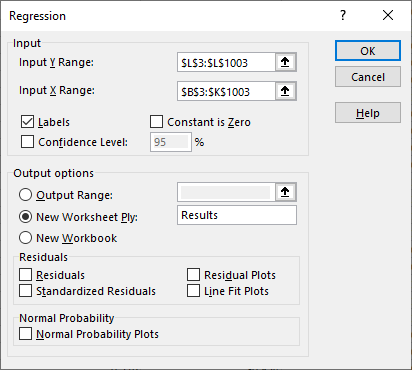
In the Regression dialog box, make the following selections:
1. The Input Y Range is the range of cells containing the maximum SWE data (including the data label).
2. The Input X Range is the range of cells containing the standardized sampled parameters (including the data labels).
3. Check the Labels box to indicate that data labels were included in the Y and X ranges.
4. Under the Output Options, enter Results in the field next to New Worksheet Ply to save the regression analysis results in a new tab named Results.
The Regression dialog box should resemble the figure below. Click the OK button perform the regression analysis.

Analyze Results

Navigate to the Results tab in Excel. The bottom table (boxed in red in the figure below) shows the results of the regression analysis. The coefficients are used to develop a linear regression of the general form:

$\begin{array}{l}y = ax + b\end{array}$

where $\begin{array}{l}a\end{array}$ is the regression coefficient and $\begin{array}{l}b\end{array}$ is the intercept. In this tutorial, 10 parameters were evaluated. Therefore, the linear regression takes the following form:

$\begin{array}{l}y = a_1x_1 + a_2x_2 + a_3x_3 + a_4x_4 + a_5x_5 + a_6x_6 + a_7x_7 + a_8x_8 + a_9x_9 + a_1_0x_1_0 + b\end{array}$

A negative regression coefficient means that smaller parameter values increase the maximum SWE and a positive regression coefficient means that larger parameter values increase the maximum SWE. The P-value indicates whether the dependent variable is statistically significant. Low P-values and high coefficient values indicate that the parameter has a significant impact on the dependent variable, or model output.

Excel regression analysis results

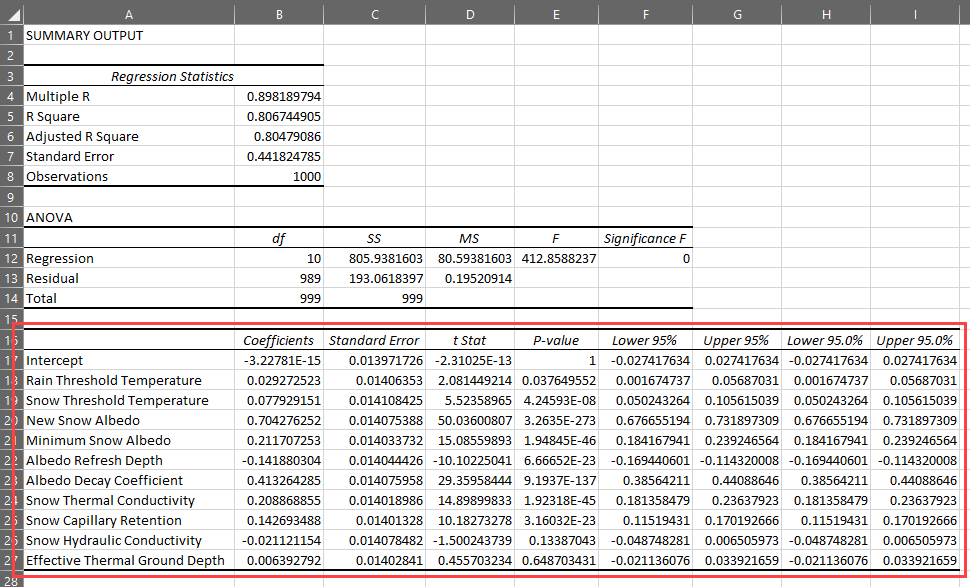
Select the 10 parameter labels and the corresponding regression coefficients.
Navigate to the Insert tab and select Recommended Charts in the Charts section. Select the Clustered Bar option. Click the OK button. The plot should look similar to the figure below.

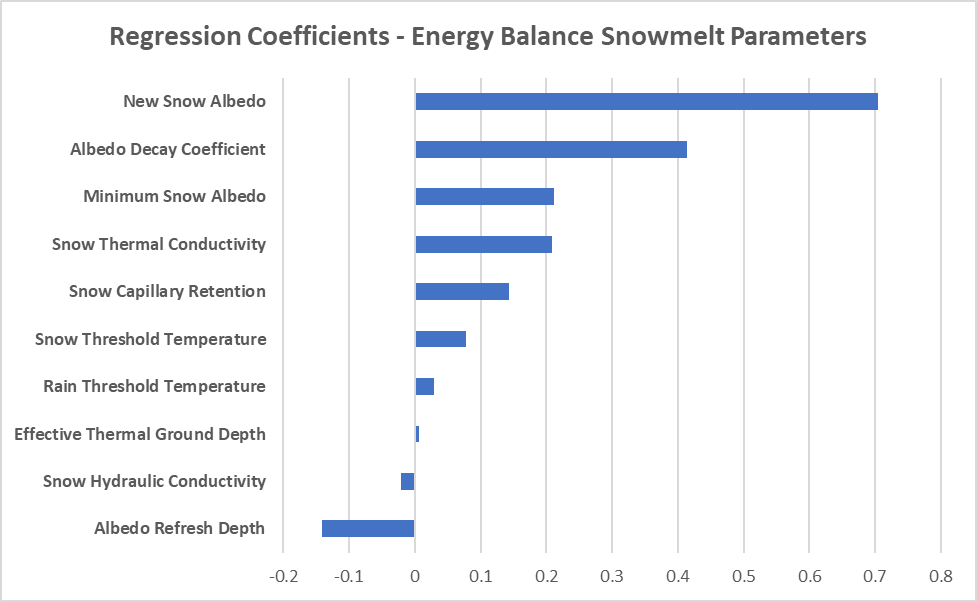
The results of this parameter sensitivity analysis are specific to the Swamp Angel Study Plot. The regression coefficients for Energy Budget snowmelt parameters will vary by location. A site-specific parameter sensitivity analysis should be performed for your modeling domain.

From the tornado chart above, it is easy to tell that the parameters with the greatest impact on the maximum SWE output relate to the albedo of the snowpack. Albedo is the reflectivity of a surface to short-wave radiation. A high albedo value means that more incident energy is reflected by the snowpack. The New Snow Albedo has the largest positive regression coefficient. A large New Snow Albedo means that more incident energy is reflected, resulting in less snowmelt. The Albedo Decay Coefficient also has a large positive regression coefficient. The Albedo Decay is the coefficient used in an exponential decay function to describe the decrease in albedo as the snowpack ages. A large Albedo Decay Coefficient means that the snowpack albedo decays slowly. The Albedo Refresh Depth has a negative regression coefficient. The Albedo Refresh Depth is the depth of fresh snow required to reset the albedo to the New Snow Albedo value. A small Albedo Refresh Depth means that a small depth of freshly accumulated snow is required to reset the snowpack albedo to the New Snow Albedo.
Another way to evaluate model results is to compare individual model parameters to maximum SWE. Two parameters were selected for further analysis: Snow Hydraulic Conductivity and New Snow Albedo. The first plot is a comparison between the standardized Snow Hydraulic Conductivity and standardized Maximum SWE. The second plot is a comparison between the standardized New Snow Albedo and standardized Maximum SWE. The figures show that New Snow Albedo has a large impact on maximum SWE while Snow Hydraulic Conductivity has very little impact on maximum SWE.

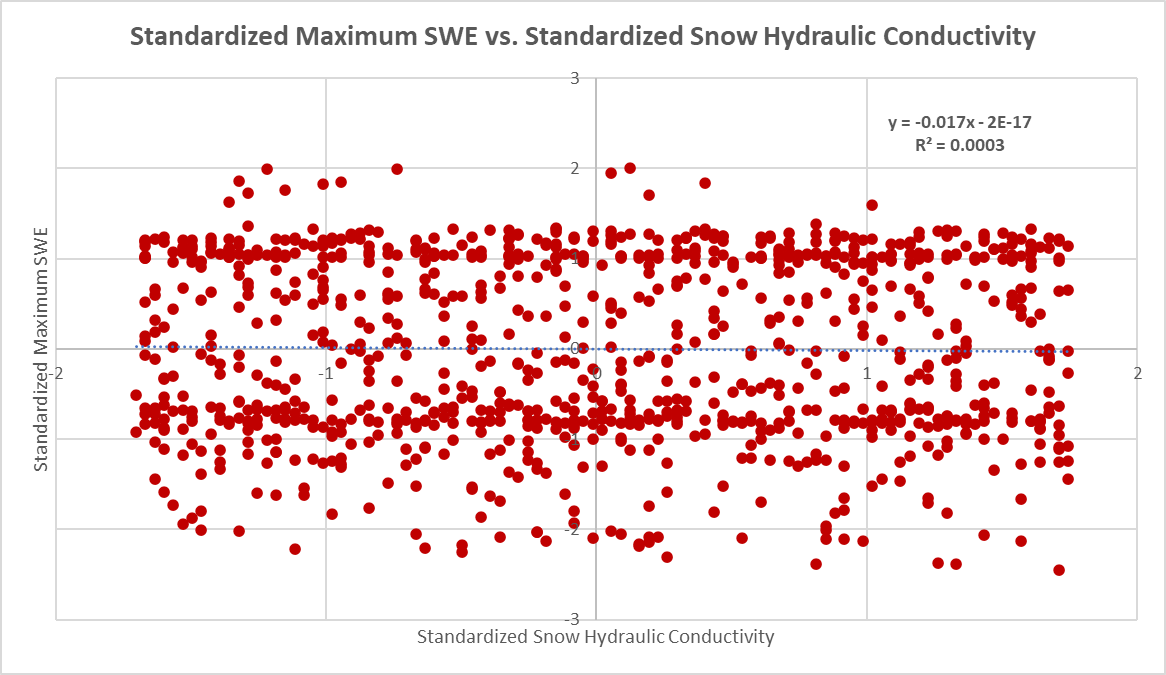
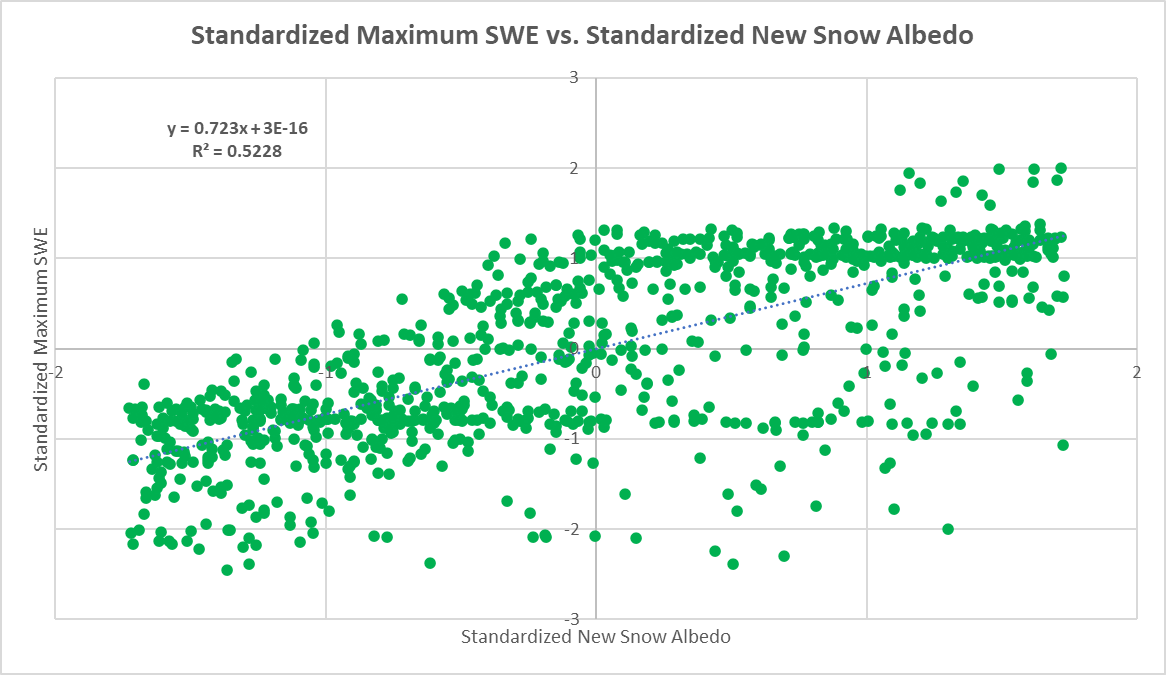
The results of the regression analysis can inform calibration efforts. In calibrating the Swamp Angel model, the focus should be on parameters related to albedo, such as New Snow Albedo, Minimum Snow Albedo, Albedo Refresh Depth, and Albedo Decay Coefficient. In addition, Snow Thermal Conductivity has a relatively large impact on the SWE results. The Excel spreadsheet used to perform the regression analysis is included below.