Download PDF
Download page Introduction to Applying the Differential Evolution Optimization Search Method.
Introduction to Applying the Differential Evolution Optimization Search Method
Last Modified: 2025-04-11 05:05:49.409
HEC-HMS version 4.13-alpha was used to create this example. You can open the example project with HEC-HMS v4.13-alpha or a newer version.
Project Files
 Bald_Eagle_Creek_Initial.zip
Bald_Eagle_Creek_Initial.zip Bald_Eagle_Creek_Final.zip
Bald_Eagle_Creek_Final.zip
Return to Applying the Differential Evolution Optimization Search Method for Single Event Calibration.
Background
Automated optimization can be a valuable tool, but it should not replace an understanding of the software, modeling methods and assumptions, impacts from individual model parameters, and knowledge of the watershed. A modeler should not rely solely on an automated optimization tool, otherwise unrealistic parameter values or parameter combinations are possible. Understanding the runoff response for a watershed, parameter impacts, and reasonable range of parameter values are required to successfully set up an optimization trial and critically evaluate results. An optimization routine relies on an objective function to evaluate how well the simulated model results meet the modeling goal, which is in general to accurately reproduce a historical event. Objective functions reduce the judgement of the model's performance to a single number. Different objective functions summarize the model performance in different ways, and emphasize different things, but no objective function can reproduce the judgment of an expert modeler.
An HEC-HMS Optimization Trial is a simulation type that can be used to identify reasonable model parameters which improve the ability of a model application to predict the precipitation runoff response. An Optimization Trial includes a Basin Model, Meteorological Model, and information about the simulation time window and time step. The trial also includes selections for the objective function, search method, and parameter adjustments. Optimization involves automated parameter adjustments that improves the objective function. The objective functions measure the goodness of fit between the simulated results and observed data. The search method is responsible making parameter adjustment as the trial searches for an optimal parameter set.
The Differential Evolution search method was added in HEC-HMS version 4.9. This search method is more robust than the Univariate gradient and Simplex search methods. The Differential Evolution search has more parameter sets that span the parameter space and the search varies in a random method, instead of the deterministic approach the other search methods follow. It is more likely that the Differential Evolution search method will find a global optimum parameter set due to the increased number of parameter sets (referred to as samples within the population) and random search component.
In this tutorial, you will see different options for applying the Differential Evolution search method and how to evaluate results from the optimization trial.
Bald Eagle Creek watershed
The Bald Eagle Creek watershed is used throughout the tutorial. Foster Joseph Sayers Dam is located on Bald Eagle Creek in Centre County, PA (shown below). Sayers Dam is about 14 miles upstream of the confluence of Bald Eagle Creek and the West Branch Susquehanna River at Lock Haven, PA.
 Location of Bald Eagle Creek Watershed
Location of Bald Eagle Creek Watershed
You will see two Basin Models when you open the example project. The BaldEagleCk_Sept2004 basin model is the uncalibrated model and the BaldEagleCk_Sept_Calib is the calibrated basin model. The drainage area upstream of Sayers Dam (336.8 square miles) was divided into three subbasins, SpringCk_S10, BaldEagleCk_S40, and BaldEagleCk_S30. The original model was simplified for this workshop to only include the SpringCk_S10 subbasin and the observed flow at the SpringCk_gage, as shown in the figure below.
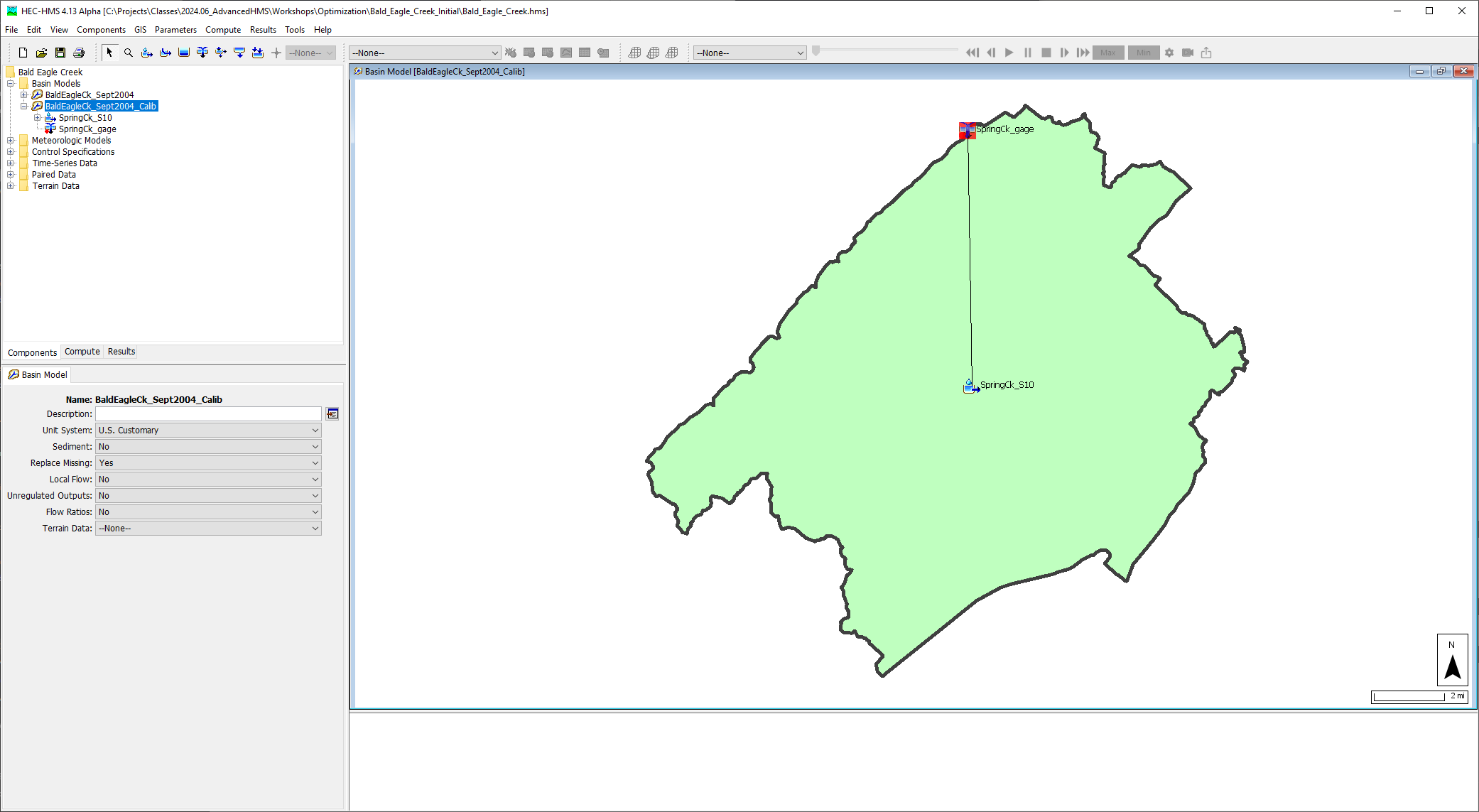 Bold Eagle Creek HMS Project
Bold Eagle Creek HMS Project
The September 2004 flood event was selected for this example. The figure below shows preliminary results and observed flow at the SpringCk_gage junction in the BaldEagleCk_Sept2004 basin model (Sept2004 simulation run). Results were generated by an uncalibrated model. Based on differences in the computed flow magnitude, time, and shape, the loss, transform and baseflow parameters needed to be adjusted from initial estimates.
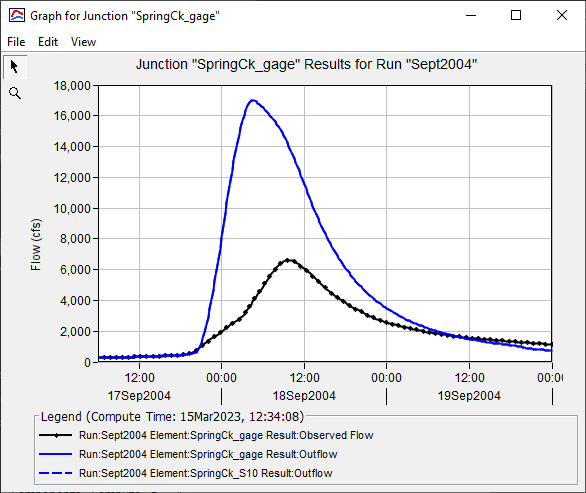 Uncalibrated Model Results
Uncalibrated Model Results
The figure below shows modeled and computed results from the BaldEagleCk_Sept2004_Calib basin model after manual calibration (Sept2004 Calibrate simulation run). Parameter values were adjusted within reason to improve the simulated peak flow, total runoff volume, and time of peak flow.
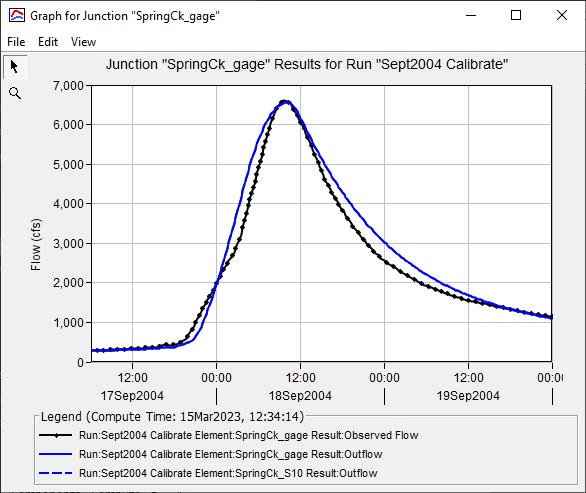 Calibrated Model Results
Calibrated Model Results
The figures below show the calibration summaries for both the Sept2004 and Sept2004 Calibrate simulation runs. Model performance is in the very good range after the model was calibrated to the flood event.
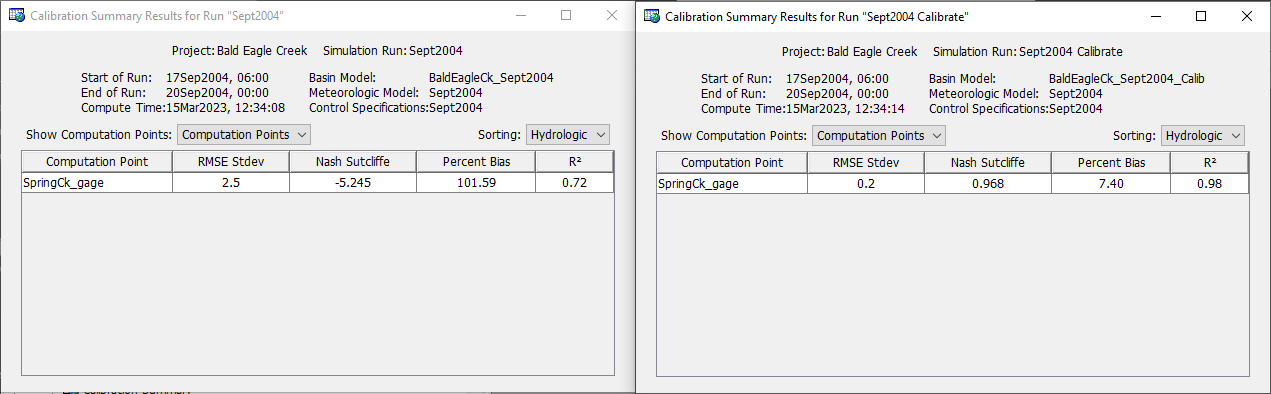 Calibration Summay Results for Uncalibrated and Calibrated Models
Calibration Summay Results for Uncalibrated and Calibrated Models
The following table contains the initial parameter estimates and final parameter values after manual calibration of the SpringCk_S10 subbasin. Notice the initial loss and initial baseflow values did not change. Initial states were determined by running a few iterations of the model and setting the values so that the model results matched the initial baseflow and the initiation of runoff. There are parameter interactions as some parameter impact similar aspects of the runoff response. For example, the constant loss rate, Clark storage coefficient, and some groundwater parameters impact the magnitude of the computed hydrograph. The model can be simplified by relating model parameter to one another. For this example, the GW 1 coefficient was set to be equal to the Clark storage coefficient. The GW 1 Reservoir parameter (number of linear reservoirs in series with the same GW 1 coefficient) was adjusted to control the magnitude and timing of the baseflow hydrograph.
| Initial Loss (in) | 2 | 2 |
| Constant Rate (in/hr) | 0.1 | 0.38 |
| Impervious (%) | 2.3 | 2.3 |
| Time of Concentration (hr) | 8.09 | 15 |
| Storage Coefficient (hr) | 8.09 | 14 |
| GW 1 Initial Flow (cfs/mi2) | 0 | 0 |
| GW 1 Fraction | 0.1 | 0.05 |
| GW 1 Coefficient (hr) | 8.09 | 14 |
| GW 1 Reservoirs | 5 | 5 |
| GW 2 Initial Flow (cfs/mi2) | 2 | 2 |
| GW 2 Fraction | 0.1 | 0.1 |
| GW 2 Coefficient (hr) | 100 | 100 |
| GW 2 Reservoirs | 1 | 1 |
Continue to The Differential Evolution Search Method.