Momentum Equation

Conservation of momentum is expressed by Newton's second law as:

1)	$\begin{array}{l}\displaystyle \displaystyle \sum{F_x}=\frac{d\vec{M}}{dt}\end{array}$

Conservation of momentum for a control volume states that the net rate of momentum entering the volume (momentum flux) plus the sum of all external forces acting on the volume be equal to the rate of accumulation of momentum. This is a vector equation applied in the x‑direction. The momentum flux (MV) is the fluid mass times the velocity vector in the direction of flow. Three forces will be considered: (1) pressure, (2) gravity and (3) boundary drag, or friction force.

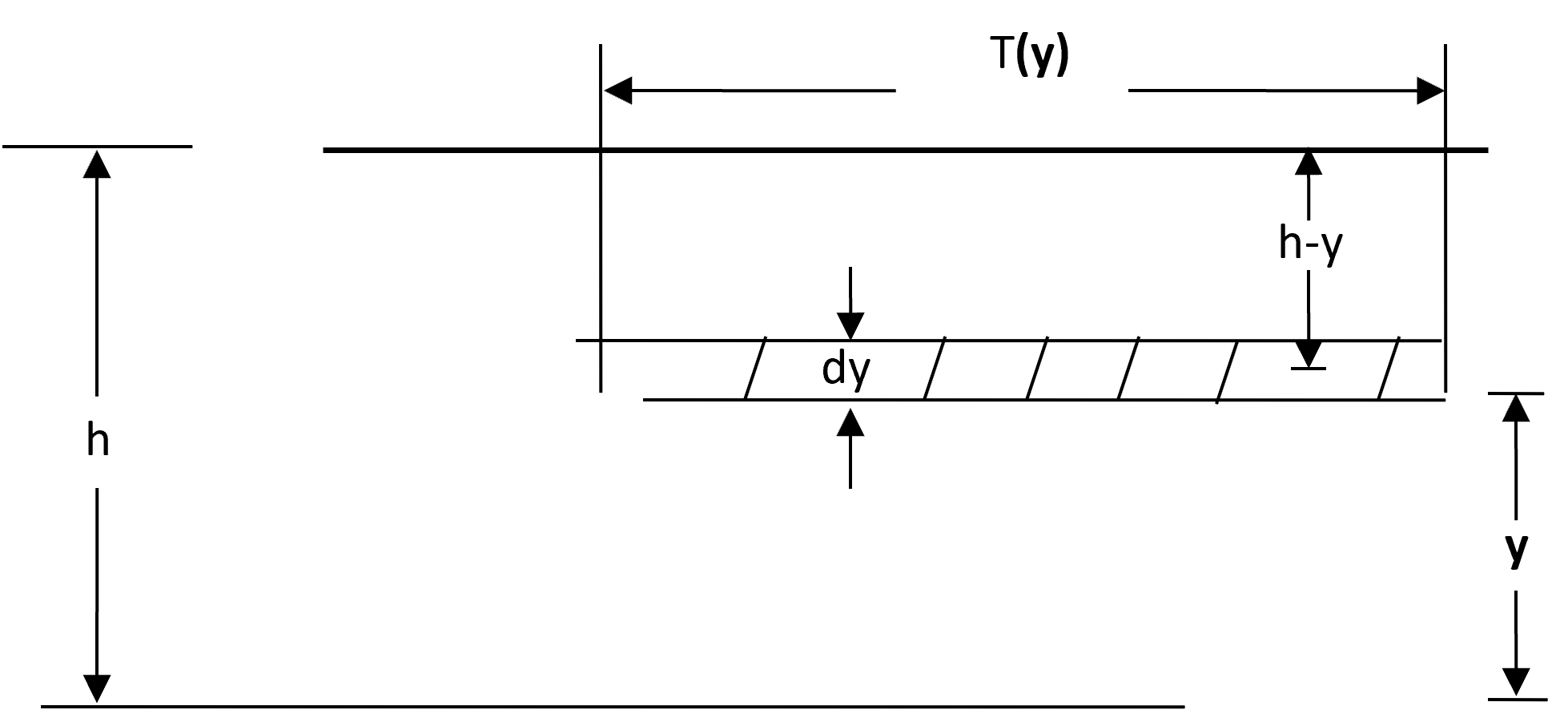
Pressure forces: The figure below illustrates the general case of an irregular cross section. The pressure distribution is assumed to be hydrostatic (pressure varies linearly with depth) and the total pressure force is the integral of the pressure-area product over the cross section. After Shames (1962), the pressure force at any point may be written as:

2)	$\begin{array}{l}\displaystyle \displaystyle F_p = \int_0^h \rho g(h-y)T(y)dy\end{array}$

Symbol	Description	Units
$\begin{array}{l}h\end{array}$	depth
$\begin{array}{l}y\end{array}$	distance above the channel invert
$\begin{array}{l}T(y)\end{array}$	width function which relates the cross section width to the distance above the channel invert

If $\begin{array}{l}F_p\end{array}$ is the pressure force in the x-direction at the midpoint of the control volume, the force at the upstream end of the control volume may be written as

3)	$\begin{array}{l}\displaystyle \displaystyle F_p - \frac{\partial F_p}{\partial x}\frac{\Delta x}{2}\end{array}$

and at the downstream end as:

4)	$\begin{array}{l}\displaystyle \displaystyle F_p + \frac{\partial F_p}{\partial x}\frac{\Delta x}{2}\end{array}$

Illustration of Terms Associated with Definition of Pressure Force

The sum of the pressure forces for the control volume may therefore be written as:

5)	$\begin{array}{l}\displaystyle \displaystyle F_{Pn}= \left\| F_P - \frac{\partial F_P}{\partial x} \frac{\Delta x}{2} \right\| - \left\| F_P + \frac{\partial F_P}{\partial x} \frac{\Delta x}{2} \right\| + F_B\end{array}$

Where $\begin{array}{l}F_{Pn}\end{array}$ is the net pressure force for the control volume, and $\begin{array}{l}F_B\end{array}$ is the force exerted by the banks in the x-direction on the fluid. This may be simplified to:

6)	$\begin{array}{l}\displaystyle \displaystyle F_{Pn}=- \frac{\partial F_P}{\partial x} \Delta x + F_B\end{array}$

Differentiating (2) using Leibnitz's Rule and then substituting in (6) results in:

7)	$\begin{array}{l}\displaystyle \displaystyle F_{Pn}=- \rho g \Delta x \left[ \frac{\partial h}{\partial x} \int_0^hT(y)dy + \int_0^h (h-y) \frac{\partial T(y)}{\partial x}dy \right] +F_B\end{array}$

The first integral in (7) is the cross-sectional area, $\begin{array}{l}A\end{array}$ . The second integral (multiplied by $\begin{array}{l}-\rho g \Delta x\end{array}$ ) is the pressure force exerted by the fluid on the banks, which is exactly equal in magnitude, but opposite in direction to $\begin{array}{l}F_B\end{array}$ . Hence the net pressure force may be written as:

8)	$\begin{array}{l}\displaystyle \displaystyle F_{Pn}=- \rho gA\frac{\partial h}{\partial x} \Delta x\end{array}$

Gravitational force: The force due to gravity on the fluid in the control volume in the x-direction is:

9)	$\begin{array}{l}\displaystyle \displaystyle F_g = \rho gAsin\theta \Delta x\end{array}$

here $\begin{array}{l}\theta\end{array}$ is the angle that the channel invert makes with the horizontal. For natural rivers $\begin{array}{l}\theta\end{array}$ is small and $\begin{array}{l}sin \theta \approx tan \theta = -\frac{\delta Z_0}{\delta X}\end{array}$ , where $\begin{array}{l}z_0\end{array}$ is the invert elevation. Therefore the gravitational force may be written as

10)	$\begin{array}{l}\displaystyle \displaystyle F_g =-\rho gA\frac{\partial z_0}{\partial x} \Delta x\end{array}$

This force will be positive for negative bed slopes.

Boundary drag (friction force): Frictional forces between the channel and the fluid may be written as:

11)	$\begin{array}{l}\displaystyle F_f=- \tau _0 P \Delta x\end{array}$

where $\begin{array}{l}\tau _0\end{array}$ is the average boundary shear stress (force/unit area) acting on the fluid boundaries, and $\begin{array}{l}P\end{array}$ is the wetted perimeter. The negative sign indicates that, with flow in the positive x-direction, the force acts in the negative x-direction. From dimensional analysis, $\begin{array}{l}\tau _0\end{array}$ may be expressed in terms of a drag coefficient, $\begin{array}{l}C_D\end{array}$ , as follows:

12)	$\begin{array}{l}\displaystyle \tau _0 =\rho C_D V^2\end{array}$

The drag coefficient may be related to the Chezy coefficient, $\begin{array}{l}C\end{array}$ , by the following:

13)	$\begin{array}{l}\displaystyle C_D = \frac{g}{C^2}\end{array}$

Further, the Chezy equation may be written as:

14)	$\begin{array}{l}\displaystyle V=C \sqrt{RS_f}\end{array}$

Substituting (12), (13), and (14) into (11), and simplifying, yields the following expression for the boundary drag force:

15)	$\begin{array}{l}\displaystyle F_f =-\rho g AS_f \Delta x\end{array}$

where $\begin{array}{l}S_f\end{array}$ is the friction slope, which is positive for flow in the positive x-direction. The friction slope must be related to flow and stage. Traditionally, the Manning and Chezy friction equations have been used. Since the Manning equation is predominantly used in the United States, it is also used in HEC-RAS. The Manning equation is written as:

16)	$\begin{array}{l}\displaystyle \displaystyle S_f=\frac{Q \left\| Q \right\| n^2}{2.208 R^{4/3} A^2}\end{array}$

Symbol	Description	Units
$\begin{array}{l}R\end{array}$	hydraulic radius and n is the Manning friction coefficient

Momentum flux: With the three force terms defined, only the momentum flux remains. The flux entering the control volume may be written as:

17)	$\begin{array}{l}\displaystyle \displaystyle \rho \left[ QV - \frac{\partial QV}{\partial x} \frac{\Delta x}{2} \right]\end{array}$

and the flux leaving the volume may be written as:

18)	$\begin{array}{l}\displaystyle \displaystyle \rho \left[ QV + \frac{\partial QV}{\partial x} \frac{\Delta x}{2} \right]\end{array}$

Therefore the net rate of momentum (momentum flux) entering the control volume is:

19)	$\begin{array}{l}\displaystyle \displaystyle -\rho \frac{\partial (QV)}{\partial x} \Delta x\end{array}$

Since the momentum of the fluid in the control volume is $\begin{array}{l}\rho Q \Delta x\end{array}$ , the rate of accumulation of momentum may be written as:

20)	$\begin{array}{l}\displaystyle \displaystyle \frac{\partial}{\partial t} \left( \rho Q \Delta x \right) = \rho \Delta x \frac{\partial Q}{\partial t}\end{array}$

Restating the principle of conservation of momentum:

The net rate of momentum (momentum flux) entering the volume (19) plus the sum of all external forces acting on the volume [(8) + (10) + (15)] is equal to the rate of accumulation of momentum (20). Hence:

21)	$\begin{array}{l}\displaystyle \displaystyle \rho \Delta x \frac{\partial Q}{\partial t} =-\rho \frac{\partial (QV) }{\partial x} \Delta x - \rho gA \frac{\partial h}{\partial x} \Delta x - \rho gA\frac{\partial z_0}{\partial x}\Delta x - \rho gAS_f \Delta x\end{array}$

The elevation of the water surface, $\begin{array}{l}z\end{array}$ , is equal to $\begin{array}{l}z_0 +h\end{array}$ . Therefore:

22)	$\begin{array}{l}\displaystyle \displaystyle \frac{\partial z_z}{\partial x} = \frac{\partial h}{\partial x} + \frac{\partial z_0}{\partial x}\end{array}$

where $\begin{array}{l}\partial z / \partial x\end{array}$ is the water surface slope. Substituting (22) into (21), dividing through by $\begin{array}{l}\rho \Delta x\end{array}$ and moving all terms to the left yields the final form of the momentum equation:

23)	$\begin{array}{l}\displaystyle \displaystyle \frac{\partial Q}{\partial t} + \frac{\partial (QV) }{\partial x} +gA \left( \frac{\partial z_s}{\partial x} + S_f \right) =0\end{array}$