Low Flow Computations

Low flow exists when the flow going through the bridge opening is open channel flow (water surface below the highest point on the low chord of the bridge opening). For low flow computations, the program first uses the momentum equation to identify the class of flow. This is accomplished by first calculating the momentum at critical depth inside the bridge at the upstream and downstream ends. The end with the higher momentum (therefore most constricted section) will be the controlling section in the bridge. If the two sections are identical, the program selects the upstream bridge section as the controlling section. The momentum at critical depth in the controlling section is then compared to the momentum of the flow downstream of the bridge when performing a subcritical profile (upstream of the bridge for a supercritical profile). If the momentum downstream is greater than the critical depth momentum inside the bridge, the class of flow is considered to be completely subcritical (i.e., class A low flow). If the momentum downstream is less than the momentum at critical depth, in the controlling bridge section, then it is assumed that the constriction will cause the flow to pass through critical depth and a hydraulic jump will occur at some distance downstream (i.e., class B low flow). If the profile is completely supercritical through the bridge, then this is considered class C low flow.

Class A Low Flow

Class A low flow exists when the water surface through the bridge is completely subcritical (i.e., above critical depth). Energy losses through the expansion (sections 2 to 1) are calculated as friction losses and expansion losses. Friction losses are based on a weighted friction slope times a weighted reach length between sections 1 and 2. The weighted friction slope is based on one of the four available alternatives in the HEC-RAS, with the average-conveyance method being the default. This option is user selectable. The average length used in the calculation is based on a discharge-weighted reach length. Energy losses through the contraction (sections 3 to 4) are calculated as friction losses and contraction losses. Friction and contraction losses between sections 3 and 4 are calculated in the same way as friction and expansion losses between sections 1 and 2.

There are four methods available for computing losses through the bridge (sections 2 to 3):

Energy Equation (standard step method)
Momentum (Prismatic) Method
Momentum (General) Method
Yarnell Equation
FHWA WSPRO method

The user can select any or all of these methods to be computed. This allows the modeler to compare the answers from several techniques all in a single execution of the program. If more than one method is selected, the user must choose either a single method as the final solution or direct the program to use the method that computes the greatest energy loss through the bridge as the final solution at section 3. Minimal results are available for all the methods computed, but detailed results are available for the method that is selected as the final answer. A detailed discussion of each method follows:

Energy Equation (Standard Step Method)

The energy-based method treats a bridge in the same manner as a natural river cross-section, except the area of the bridge below the water surface is subtracted from the total area, and the wetted perimeter is increased where the water is in contact with the bridge structure. As described previously, the program formulates two cross-sections inside the bridge by combining the ground information of sections 2 and 3 with the bridge geometry. As shown in the figure below, for the purposes of discussion, these cross-sections will be referred to as sections BD (Bridge Downstream) and BU (Bridge Upstream).

The sequence of calculations starts with a standard step calculation from just downstream of the bridge (section 2) to just inside of the bridge (section BD) at the downstream end. The program then performs a standard step through the bridge (from section BD to section BU). The last calculation is to step out of the bridge (from section BU to section 3).

The energy-based method requires Manning's n values for friction losses and contraction and expansion coefficients for transition losses. The estimate of Manning's n values is well documented in many hydraulics text books, as well as several research studies. Basic guidance for estimating roughness coefficients is provided in "Basic Data Requirements" of this manual. Contraction and expansion coefficients are also provided in "Basic Data Requirements", as well as in earlier sections of this chapter. Detailed output is available for cross-sections inside the bridge (sections BD and BU) as well as the user entered cross-sections (sections 2 and 3).

Momentum (Prismatic) Method

The Momentum (Prismatic) method is based on performing a momentum balance from cross-section 2 to cross-section 3. The momentum balance is performed in three steps going from 2 to BD, BD to BU, and BU to 3. The first step is to perform a momentum balance from cross-section 2 to cross-section BD inside the bridge. The discrete momentum balance can be written as

1)	$\begin{array}{l}\displaystyle \displaystyle A_{BD} \overline{Y}_{BD} + \frac{\beta _{BD} Q^2_{BD}}{g A_{BD}} = A_2 \overline{Y}_2 + \frac{\beta _2 Q^2_2}{gA_2} -A_{P_{BD}} \overline{P}_{BD} + F_f - W_x\end{array}$

Symbol	Description	Units
$\begin{array}{l}A_2, A_{BD}\end{array}$	Active flow area at section 2 and BD, respectively	L²
$\begin{array}{l}A_{P_{BD}}\end{array}$	Obstructed area of the pier on downstream side	L²
$\begin{array}{l}\overline{Y}_2 , \overline{Y}_{BD}\end{array}$	Vertical distance from water surface to center of gravity of flow area A₂ and A_BD, respectively	L
$\begin{array}{l}\overline{Y}_{P_{BD}}\end{array}$	Vertical distance from water surface to center gravity of wetted pier area on downstream side	L
$\begin{array}{l}\beta _2, \beta _{BD}\end{array}$	Velocity weighting coefficients for momentum equation	-
$\begin{array}{l}Q_2, Q_{BD}\end{array}$	Discharge	L³/T
$\begin{array}{l}g\end{array}$	Gravitational acceleration
$\begin{array}{l}F_f\end{array}$	External force due to friction, per unit weight of water
$\begin{array}{l}W_x\end{array}$	Force due to weight of water n the direction of flow, per unit weight of water

The second step is a momentum balance from section BD to BU (see figure above). The equation for this step is as follows:

2)	$\begin{array}{l}\displaystyle \displaystyle A_{BU} \overline{Y} _{BU} + \frac{\beta _{BU} Q^2_{BU}}{gA_{BU}} = A_{BD} \overline{Y}_{BD} + \frac{\beta _{BD} Q^2_{BD}}{gA_{BD}} + F_f -W_x\end{array}$

The final step is a momentum balance from section BU to section 3 (see figure above). The equation for this step is as follows:

3)	$\begin{array}{l}\displaystyle \displaystyle A_3 \overline{Y} _3 + \frac{\beta _3 Q^2_3}{gA_3} = A_{BU} \overline{Y}_{BU} + \frac{\beta _{BD} Q^2_{BD}}{gA_{BD}} +A_{P_{BU}} \overline{Y}_{P_{BU}} + \frac{1}{2} C_D \frac{A_{P_{BU}} Q^2_3}{gA^2_3} + F_f -W_x\end{array}$

where $\begin{array}{l}C_D\end{array}$ is a coefficient for flow going around the piers. Guidance on selecting drag coefficients can be found under the table below.

The momentum balance method requires the use of roughness coefficients for the estimation of the friction force and a drag coefficient for the force of drag on piers. As mentioned previously, roughness coefficients are described in "Basic Data Requirements" of this manual. Drag coefficients are used to estimate the force due to the water moving around the piers, the separation of the flow, and the resulting wake that occurs downstream. Drag coefficients for various cylindrical shapes have been derived from experimental data (Lindsey 1938). Typical drag coefficients that can be used for piers are shown in the table below.

Pier Shape Drag Coefficients

Pier Shape	Drag Coefficient C_D
Circular pier	1.20
Elongated piers with semi-circular ends	1.33
Elliptical piers with 2:1 length to width	0.60
Elliptical piers with 4:1 length to width	0.32
Elliptical piers with 8:1 length to width	0.29
Square nose piers	2.00
Triangular nose with 30 degree angle	1.00
Triangular nose with 60 degree angle	1.39
Triangular nose with 90 degree angle	1.60
Triangular nose with 120 degree angle	1.72

The Momentum (Prismatic) method is the legacy approach and may give incorrect results if the bounding cross-sections are significantly different (this method is sensitive to bed slope). The hydraulic properties should be verified for consistency for the low flow portion of the hydraulic property curves. In the figure below, an example shows an erroneous head loss for all of the low flow curves starting with the first computed flow and shift subsequent points on the curve upward. This will happen if the flow areas are significantly different for the headwater and tailwater for the bridge.

The Momentum (General) method was implemented in HEC-RAS 6.7 and is recommended. This method computes the losses in a steady-state implementation of the general 1D momentum approach and works on both natural and prismatic channels. The Prismatic (Legacy) method steps though a structure and solves by a force/momentum balance (traditional approach for modeling hydraulic jumps) and can be overly sensitive to cross-section shape and bed slope. Both the Momentum (General) and Prismatic (Legacy) methods account for pier impact losses. A comparison of bridge curves for the two methods is shown in the figure below.

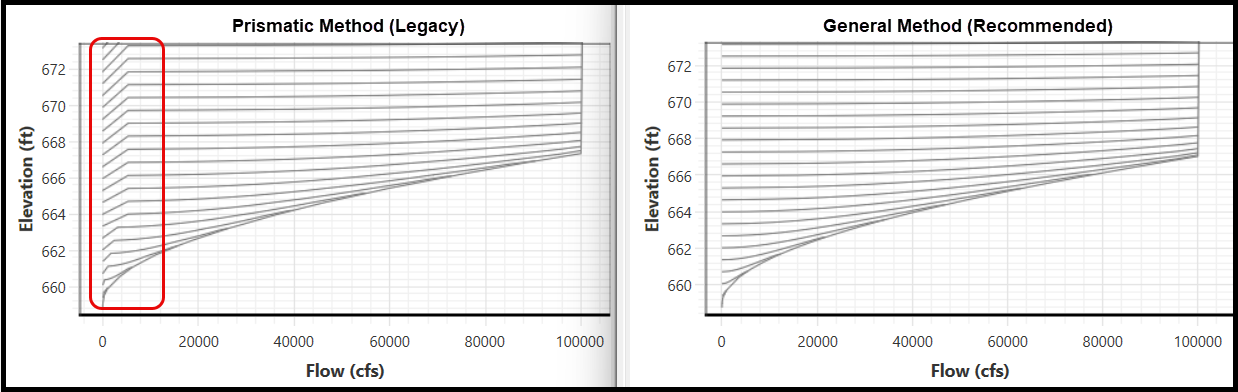
The momentum method provides detailed output for the cross-sections inside the bridge (BU and BD) as well as outside the bridge (2 and 3). The user has the option of turning the friction and weight force components on or off. The default is to include the friction force but not the weight component. The computation of the weight force is dependent upon computing a mean bed slope through the bridge. Estimating a mean bed slope can be very difficult with irregular cross-section data. A bad estimate of the bed slope can lead to large errors in the momentum solution. The user can turn this force on if they feel that the bed slope through the bridge is well behaved for their application.

During the momentum calculations, if the water surface (at sections BD and BU) comes into contact with the maximum low chord of the bridge, the momentum balance is assumed to be invalid and the results are not used.

Momentum (General) Method

The Momentum (General) Method is the preferred momentum method. The method is based on a steady form of the 1D unsteady flow momentum equation. The Momentum (Prismatic) Method is legacy method and is only recommended for prismatic channels.

The momentum method is based on performing a momentum balance from cross-section 2 to cross-section 3. The momentum balance is performed in three steps. From BD to 2, 2 to BU, and BU to 3. The first step is to perform a momentum balance from cross-section 2 to cross-section BD inside the bridge. The discrete momentum balance can be written as

4)	$\begin{array}{l}\displaystyle \displaystyle Q \left( \beta_{BD} V_{BD} - \beta_{2} V_{2} \right) + g \overline{A} \left(Z_{BD} - Z_2 \right) = -g \overline{A} \overline{S}_f L\end{array}$

Symbol	Description	Units
$\begin{array}{l}\beta_{BD}, \beta_{2}\end{array}$	Velocity weighting coefficients at cross-sections BD and 2	-
$\begin{array}{l}V_{BD}, V_{2}\end{array}$	Velocities at cross-sections BD and 2	L/T
$\begin{array}{l}Z_{BD}, Z_2\end{array}$	Water surfaces at cross-sections BD and 2	L
$\begin{array}{l}\overline{S}_f\end{array}$	Cross-sectionally averaged friction slope	-
$\begin{array}{l}\beta _2, \beta _{BD}\end{array}$	Velocity weighting coefficients for momentum equation.	-
$\begin{array}{l}Q\end{array}$	Discharge	L³/T
$\begin{array}{l}g\end{array}$	Gravitational acceleration

The second step of the general momentum method is from cross-sections BD to BU. The discrete momentum balance is same as the previous

5)	$\begin{array}{l}\displaystyle \displaystyle Q \left( \beta_{BU} V_{BU} - \beta_{BD} V_{BD} \right) + g \overline{A} \left(Z_{BU} - Z_{BD} \right) = -g \overline{A} \overline{S}_f L\end{array}$

The final and third step of the general momentum method is cross-sections BU to 3. This step includes is similar to the previous two steps but includes an pier loss term

6)	$\begin{array}{l}\displaystyle \displaystyle Q \left( \beta_{3} V_{3} - \beta_{BU} V_{BU} \right) + g \overline{A} \left(Z_{3} - Z_{BU} \right) = -g \overline{A} \overline{S}_f L - \frac{1}{2} C_D A_{P_{BU}} V_3^2\end{array}$

where $\begin{array}{l}C_D\end{array}$ is the pier drag coefficient. Guidance on selecting drag coefficients is the same as in the Momentum (Prismatic) method described above.

Yarnell Equation

The Yarnell method is only appropriate for trapezoidal channels with piers.

The Yarnell equation is an empirical equation that is used to predict the change in water surface from just downstream of the bridge (section 2 of the figure above) to just upstream of the bridge (section 3). The equation is based on approximately 2600 lab experiments in which the researchers varied the shape of the piers, the width, the length, the angle, and the flow rate. The Yarnell equation is as follows (Yarnell, 1934):

7)	$\begin{array}{l}\displaystyle \displaystyle H_{3-2} = 2K(K+10 \omega -0.6)( \alpha +15 \alpha ^4) \frac{V^2}{2g}\end{array}$

Symbol	Description	Units
$\begin{array}{l}H_{3-2}\end{array}$	Drop in water surface elevation from section 3 to 2
$\begin{array}{l}K\end{array}$	Yarnell's pier shape coefficients
$\begin{array}{l}\omega\end{array}$	Ratio of velocity head to depth at section 2
$\begin{array}{l}\alpha\end{array}$	Obstructed area of the piers divided by the total unobstructed area at section 2
$\begin{array}{l}V^2\end{array}$	Velocity downstream at section 2

The computed upstream water surface elevation (section 3) is simply the downstream water surface elevation plus $\begin{array}{l}H_{3-2}\end{array}$ . With the upstream water surface known the program computes the corresponding velocity head and energy elevation for the upstream section (section 3). When the Yarnell method is used, hydraulic information is only provided at cross-sections 2 and 3 (no information is provided for sections BU and BD).

The Yarnell equation is sensitive to the pier shape (K coefficient), the pier obstructed area, and the velocity of the water. The method is not sensitive to the shape of the bridge opening, the shape of the abutments, or the width of the bridge. Because of these limitations, the Yarnell method should only be used at bridges where the majority of the energy losses are associated with the piers. When Yarnell's equation is used for computing the change in water surface through the bridge, the user must supply the Yarnell pier shape coefficient, K. The following table gives values for Yarnell's pier coefficient, K, for various pier shapes:

Pier Shape Yarnell K Coefficients

Pier Shape	Yarnell K Coefficient
Semi-circular nose and tail	0.90
Twin-cylinder piers with connecting diaphragm	0.95
Twin-cylinder piers without diaphragm	1.05
90 degree triangular nose and tail	1.05
Square nose and tail	1.25
Ten pile trestle bent	2.50

FHWA WSPRO Method

The low flow hydraulic computations of the Federal Highway Administration's (FHWA) WSPRO computer program, has been adapted as an option for low flow hydraulics in HEC-RAS. The WSPRO methodology had to be modified slightly in order to fit into the HEC-RAS concept of cross-section locations around and through a bridge.

The WSPRO method computes the water surface profile through a bridge by solving the energy equation. The method is an iterative solution performed from the exit cross-section (1) to the approach cross-section (4). The energy balance is performed in steps from the exit section (1) to the cross-section just downstream of the bridge (2); from just downstream of the bridge (2) to inside of the bridge at the downstream end (BD); from inside of the bridge at the downstream end (BD) to inside of the bridge at the upstream end (BU); From inside of the bridge at the upstream end (BU) to just upstream of the bridge (3); and from just upstream of the bridge (3) to the approach section (4). A general energy balance equation from the exit section to the approach section can be written as follows:

8)	$\begin{array}{l}\displaystyle \displaystyle h_4 + \frac{a_4 V^2_4}{2g} = h_1 + \frac{a_1 V^2_1}{2g} +h_f +h_e\end{array}$

Symbol	Description	Units
$\begin{array}{l}h_1\end{array}$	Water surface elevation at section 1
$\begin{array}{l}V_1\end{array}$	Velocity at section 1
$\begin{array}{l}h_4\end{array}$	Water surface elevation at section 4
$\begin{array}{l}V_4\end{array}$	Velocity at section 4
$\begin{array}{l}h_L\end{array}$	Energy losses from section 4 to 1

The incremental energy losses from section 4 to 1 are calculated as follows:

From Section 1 to 2

Losses from section 1 to section 2 are based on friction losses and an expansion loss. Friction losses are calculated using the geometric mean friction slope times the flow weighted distance between sections 1 and 2. The following equation is used for friction losses from 1 to 2:

9)	$\begin{array}{l}\displaystyle \displaystyle h_{f_{1-2}} = \frac{BQ^2}{K_2K_1}\end{array}$

Where B is the flow weighted distance between sections 1 and 2, and K₁ and K₂ are the total conveyance at sections 1 and 2 respectively. The expansion loss from section 2 to section 1 is computed by the following equation:

10)	$\begin{array}{l}\displaystyle \displaystyle h_e = \frac{Q^2}{2gA^2_1} \left[ 2 \beta _1 -a_1 -2 \beta _2 \left( \frac{A_1}{A_2} \right) + a_2 \left( \frac{A_1}{A_2} \right) ^2 \right]\end{array}$

Where α and β are energy and momentum correction factors for non-uniform flow. and β₁ are computed as follows:

11)	$\begin{array}{l}\displaystyle \displaystyle a_1 = \frac{\sum (K^3_i / A^2_i )}{K^3_T / A^2_T}\end{array}$

12)	$\begin{array}{l}\displaystyle \displaystyle \beta _1 = \frac{\sum (K^2_i / A_i )}{K^2_T / A_T}\end{array}$

$\begin{array}{l}a_2\end{array}$ and $\begin{array}{l}\beta _2\end{array}$ are related to the bridge geometry and are defined as follows:

13)	$\begin{array}{l}\displaystyle \displaystyle a_2 = \frac{1}{C^2}\end{array}$

14)	$\begin{array}{l}\displaystyle \displaystyle \beta _2 = \frac{1}{C}\end{array}$

where C is an empirical discharge coefficient for the bridge, which was originally developed as part of the Contracted Opening method by Kindswater, Carter, and Tracy (USGS, 1953), and subsequently modified by Matthai (USGS, 1968). The computation of the discharge coefficient, C, is explained in detail in appendix D of this manual.

Cross-Sections 2 to 3

Losses from section 2 to section 3 are based on friction losses only. The energy balance is performed in three steps: from section 2 to BD; BD to BU; and BU to 3. Friction losses are calculated using the geometric mean friction slope times the flow weighted distance between sections. The following equation is used for friction losses from BD to BU:

15)	$\begin{array}{l}\displaystyle \displaystyle h_{f_{(BU-BD)}} = \frac{L_BQ^2}{K_{BU}K_{BD}}\end{array}$

Where K_BU and K_BD are the total conveyance at sections BU and BD respectively, and L_B is the length through the bridge. Similar equations are used for the friction losses from section 2 to BD and BU to 3.

Cross-Sections 3 to 4

Energy losses from section 3 to 4 are based on friction losses only. The equation for computing the friction loss is as follows:

16)	$\begin{array}{l}\displaystyle \displaystyle h_{f_{(3-4)}} = \frac{L_{av}Q^2}{K_3K_4}\end{array}$

Where L_av is the effective flow length in the approach reach, and K₃ and K₄ are the total conveyances at sections 3 and 4. The effective flow length is computed as the average length of 20 equal conveyance stream tubes (FHWA, 1986). The computation of the effective flow length by the stream tube method is explained in appendix D of this manual.

Class B Low Flow

Class B low flow can exist for either subcritical or supercritical profiles. For either profile, class B flow occurs when the profile passes through critical depth in the bridge constriction. For a subcritical profile, the momentum equation is used to compute an upstream water surface (section 3 of the figure above) above critical depth and a downstream water surface (section 2) below critical depth. For a supercritical profile, the bridge is acting as a control and is causing the upstream water surface elevation to be above critical depth. Momentum is used to calculate an upstream water surface above critical depth and a downstream water surface below critical depth. If for some reason the momentum equation fails to converge on an answer during the class B flow computations, the program will automatically switch to an energy-based method for calculating the class B profile through the bridge.

Whenever class B flow is found to exist, the user should run the program in a mixed flow regime mode. If the user is running a mixed flow regime profile the program will proceed with backwater calculations upstream, and later with forewater calculations downstream from the bridge. Also, any hydraulic jumps that may occur upstream and downstream of the bridge can be located if they exist.

Class C Low Flow

Class C low flow exists when the water surface through the bridge is completely supercritical. The program can use either the energy equation or the momentum equation to compute the water surface through the bridge for this class of flow.