Copeland Method

User Guide
Video
The Copeland Method for stable channel design was developed by Dr. Ronald Copeland at the Waterways Experiment Station for use in the SAM software package (Copeland, 1994). This approach is primarily analytical on a foundation of empirically-derived equations and it uses the sediment discharge and flow depth prediction methods of Brownlie (1981) to ultimately solve for stable depth and slope, for a given channel bottom width for trapezoidal cross sections. This method assumes bed load movement occurs above the bed, not the banks, and separates hydraulic roughness into bed and bank components.

To determine the level of stability of the design channel, an inflowing sediment discharge must be established. This can be done simply by entering the upstream sediment concentration, or by entering a supply reach bottom width and slope and allowing the program to calculate the sediment discharge. Sediment concentration is given by the following:

1)	$\begin{array}{l}\displaystyle \displaystyle C=9022(F_g - F_{g0} )^{1.978} S^{0.6601} \left( \frac{R_b}{d_{50}} \right) ^{-0.3301}\end{array}$

Symbol	Description	Units
$\begin{array}{l}C\end{array}$	Sediment concentration over the bed	ppm
$\begin{array}{l}F_g\end{array}$	Grain-related Froude number
$\begin{array}{l}F_{g0}\end{array}$	Critical grain-related Froude number
$\begin{array}{l}S\end{array}$	Slope
$\begin{array}{l}R_b\end{array}$	Bed hydraulic radius
$\begin{array}{l}d_{50}\end{array}$	Median grain size

Where:

2)	$\begin{array}{l}\displaystyle \displaystyle F_g = \frac{V}{\sqrt{(s_s -1)gd_{50}}}\end{array}$

Symbol	Description	Units
$\begin{array}{l}V\end{array}$	Average channel velocity (this method assumes the average velocity for the total cross section is representative of the average velocity in each sub section).
$\begin{array}{l}s_s\end{array}$	Specific Gravity of sediment particles.

Where:

3)	$\begin{array}{l}\displaystyle \displaystyle F_{g0} = \frac{4.596 \tau ^{0.5293}_{*_0}}{S^{0.1405} \sigma ^{0.1606}}\end{array}$

4)	$\begin{array}{l}\displaystyle \tau _{*_0} =0.22Y+0.06(10)^{-7.7Y}\end{array}$

5)	$\begin{array}{l}\displaystyle Y= \left( \sqrt{s_s-1} R_g \right) ^{-0.6}\end{array}$

6)	$\begin{array}{l}\displaystyle \displaystyle R_g = \sqrt{\frac{gd^3_{50}}{v}}\end{array}$

7)	$\begin{array}{l}\displaystyle \displaystyle \sigma = \frac{1}{2} \left( \frac{d_{84}}{d_{50}} + \frac{d_{50}}{d_{16}} \right)\end{array}$

Symbol	Description	Units
$\begin{array}{l}\tau _{*_0}\end{array}$	Critical shear stress
$\begin{array}{l}R_g\end{array}$	Grain Reynolds Number
$\begin{array}{l}V\end{array}$	Kinematic viscosity
$\begin{array}{l}\sigma\end{array}$	Sediment gradation coefficient

Brownlie uses the above regression equations to equate critical shear from Shield's diagram with critical Froude number, which can ultimately be used to represent a critical velocity by substituting $\begin{array}{l}F_{g0}\end{array}$ into (2).

For the case where the Grain-related Froude Number is less than or equal to the Critical Grain-related Froude Number, the sediment concentration, C, will automatically be returned as zero, indicating no sediment bed movement.

Once the inflowing sediment concentration over the bed is determined, the total sediment concentration for the entire channel is used to size stable channel dimensions for various channel bottom widths. To do this, Brownlie's resistance equations are used:

8)	$\begin{array}{l}\displaystyle \begin{array} 1 R_b =0.2836 d_{50} q^{0.6248}_* S^{-0.2877} \sigma ^{0.08013} & , \;for \;Upper \;Regime \\ R_b =0.3724 d_{50} q^{0.6539}_* S^{-0.2542} \sigma ^{0.1050} & , \;for \;Lower \;Regime \end{array}\end{array}$

Symbol	Description	Units
$\begin{array}{l}q_*\end{array}$	dimensionless unit discharge
$\begin{array}{l}\sigma\end{array}$	sediment gradation coefficient

Where:

9)	$\begin{array}{l}\displaystyle \displaystyle q_* = \frac{VD}{\sqrt{gd^3_{50}}}\end{array}$

Upper or lower transport regime is determined using the relationship expressed in (Bed Roughness Functions:15). However, if the Grain-related Froude Number is within 0.8 to 1.25 of 1.74/S1/3, then it is considered to be in the transitional regime. Currently, a definition for a function describing the transitional transport regime is not available. The user has the choice of applying either the upper or lower regime equations in this circumstance. In the lower regime, the bed form can be composed of ribbons or ridges, ripples, dunes, bars, or simply a flat bed with transportation mostly as bed load. The transitional regime consists of washed-out dunes and sand waves, with particles transported mostly by suspension. The upper regime develops symmetrical sand waves in subcritical flow and plane bed and/or anti dunes for supercritical flow. Particles are almost entirely in suspension. If a transitional regime is realized in one or more of the solutions, recompute the stable channel dimensions using the other transport regime and compare results. Typically the upper regime is found on the rising end of a flood wave and the lower regime is found on the falling end. It is suggested that the more conservative results be used for design if the regime is not known.

Because the roughness of the side slopes is accounted for in this solution method, an assumption has to be made as to their hydraulic parameters. It is assumed that the average velocity over the side slopes is equal to the average channel velocity. With that,

10)	$\begin{array}{l}\displaystyle \displaystyle R_s = \left( \frac{Vn_s}{1.486S^{0.5}} \right)\end{array}$

and the channel area, $\begin{array}{l}A\end{array}$ , can be determined by

11)	$\begin{array}{l}\displaystyle A=R_b P_b + R_s P_s\end{array}$

Symbol	Description	Units
$\begin{array}{l}R_s\end{array}$	Hydraulic radius of the side slopes
$\begin{array}{l}n_s\end{array}$	Manning's n value of the side slopes
$\begin{array}{l}P_s\end{array}$	Wetted perimeter of the side slopes
$\begin{array}{l}R_b\end{array}$	Hydraulic radius of the bed
$\begin{array}{l}P_b\end{array}$	Bed width

The bed roughness is calculated using Brownlie's roughness predictor (Bed Roughness Functions:17).

The user can enter a median channel width to bracket the desired results or this value can be left empty, in which case, HEC-RAS will automatically compute a median channel width from the following regime equation, which is proposed in EM 1110-2-1418:

12)	$\begin{array}{l}\displaystyle B=2.0Q^{0.5}\end{array}$

Using the median channel width, HEC-RAS determines 19 other channel widths at increments of 0.1B. Stable channel geometry is then solved for each channel width. A stability curve can be analyzed by plotting the array of base widths and their corresponding stable slopes within HEC-RAS by pressing the "Stability Curve" command button after computations have been run. As shown in the figure below, it is easy to see for what slope/width channel geometries degradation, aggradation, or stabilization can be expected. It is important to note that the further away from the stability curve, the more aggradation of degradation can be expected. A second-order Lagrangian interpolation scheme is used to find the minimum stream power solution that will transport the inflowing sediment load.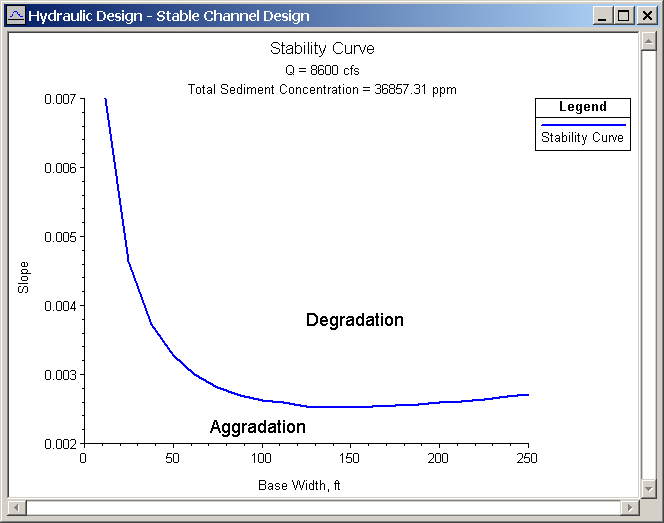

The use of k values to define roughness on the side slopes is permitted for the Copeland Method. HEC-RAS simply converts the k value to an associated Manning's n value using Strickler's equation (Bed Roughness Functions:13) with a value of 0.039 for the Strickler function, as suggested by Copeland. The bank roughness should be an accurate representation of everything that contributes to roughness on the banks. This includes channel irregularities, variations of channel cross-section shape, channel sinuosity, and vegetation. It is important to run the computations using a range of roughness values to test the sensitivity. Because, in this method, all sediment transport is assumed to occur over the bed, and not over the banks, flow distribution is very important for accuracy. This is accounted for in the bank steepness and roughness. For maximum transport, use a very steep bank with low roughness.

Sound judgment must be used when selecting the appropriate design discharge for performing a stability analysis. To date, no generally accepted discharge for stable channel design is agreed upon, therefore the use of a range of discharges is recommended. Suggested design discharges that may represent the channel forming discharge are:

2-year frequency flood (perennial streams)
10-year frequency flood (ephemeral streams)
Bankfull discharge
Effective discharge (Q that carries the most bed load sediment)

Selection of the design discharge should be made after considering the general physical characteristics of the stream, the temporal characteristics of the stream, what is the desired outcome (channel stabilization?), and any other applicable factor. It would be wise to run the calculations using a range of discharges as well as sediment inflows for a sensitivity analysis to understand how the channel reacts to different sediment and water inflow events.

As in the SAM package, HEC-RAS calculates a range of widths and slopes, and their unique solution for depth. This makes it possible to easily analyze or design stable channels. If a given slope is desired, the channel width through that reach can be adjusted to a value on the stability curve. Likewise, if a particular channel width is desired, the channel slope can be adjusted to achieve stability. If, for a given width, the slope is greater than the input valley slope, which is the maximum possible slope for the channel invert, this creates a sediment trap, which is indicate by the results. However, if the slope is less than the valley slope, the stability curve can be used to aid in adding sinuosity or the spacing of drop structures.

Because the Brownlie equations were developed from an analysis of field and laboratory data, there are limits of applicability that should be adhered to. At the least, the user needs to be aware if the limits are being exceeded. Table 12-3 presents the ranges of selected parameters of field and laboratory data used in Brownlie's research.

Table 12-3 Data Range and Applicabilities of Copeland Method

Velocity (fps)

Depth (ft)

Slope x 10³

d₅₀ x 10^-3 (ft)

Conc. (ppm)

Min

Max

Min

Max

Min

Max

Min

Max

Min

Max

Lab

0.73

6.61

0.11

1.91

0.269

16.950

0.28

4.42

10.95

39263

Field

1.20

7.95

0.35

56.7

0.010

1.799

0.28

4.72

11.70

5830

In addition, Brownlie suggests input data be restricted to the following

Table 12-4 Suggested Input Restrictions for Copeland Method

Parameter	Symbol	Restriction	Reason
Median Grain Size (ft x 10^-3)	d₅₀	0.203<d₅₀<6.56	Sand only
Geometric Standard Deviation of Bed Particles	$\begin{array}{l}\sigma\end{array}$ _g	_{$\begin{array}{l}\sigma\end{array}$ g} < 5	Eliminate bimodal grain distributions
Width to Depth Ratio	B/D	B/D > 4	Reduce sidewall effects
Relative Roughness	R_b/d₅₀	R_b/d₅₀ > 100	Eliminate shallow water effects
Concentration (ppm)	C	C>10	Accuracy problems associated with low concentration