Wind Surface Stress

The wind surface stress vector is calculated as:

1)	$\begin{array}{l}\displaystyle \tau _s = \rho _{\alpha} C_D \left\| \boldsymbol{W} _{10} \right\| \boldsymbol{W} _{10}\end{array}$

where $\begin{array}{l}\rho _{\alpha}\end{array}$ is the air density at sea level (~1.29 kg/m³), $\begin{array}{l}C_D\end{array}$ is the wind drag coefficient, $\begin{array}{l}W_{10}\end{array}$ is the 10-m height wind speed vector, $\begin{array}{l}\left| W_{10} \right|\end{array}$ is the 10-m wind velocity magnitude. The wind speed is calculated using either an Eulerian or Lagrangian reference frame as:

2)	$\begin{array}{l}\displaystyle \boldsymbol{W} _{10} = \boldsymbol{W} _{10}^E - \gamma _W \boldsymbol{V}\end{array}$

where $\begin{array}{l}\boldsymbol{W} _{10}\end{array}$ is the 10-m atmospheric wind speed relative to the solid earth (Eulerian wind speed), $\begin{array}{l}\gamma _W\end{array}$ is equal to zero for the Eulerian reference frame or one for the Lagrangian reference frame, and $\begin{array}{l}\boldsymbol{V}\end{array}$ = current velocity vector.

Winds are specified in an Eulerian reference frame with respect to the solid Earth. The Lagrangian reference frame is with respect to the moving surface water. Using the Lagrangian reference frame (see figure below), or relative wind speed, is more accurate and realistic for field applications (Bye 1985; Pacanowski 1987; Dawe and Thompson 2006), however, the option to use the Eulerian wind speed is provided for idealized cases. In addition, the Lagrangian reference frame is more stable since it introduces a drag or friction term. When the wind in the same direction of the currents the wind shear stress is lowered. When the wind and currents are in opposing directions, the wind shear stress is increased. For example, in the case of a current velocity of 1 m/s, with an opposing wind speed of 5 m/s, the Eulerian reference frame will give a surface stress proportional to (5 m/s)² = 25 m²/s², while the Lagrangian reference frame will produce a surface proportional to (5-(-1) m/s)² = 36 m²/s², which is an increase of 44%.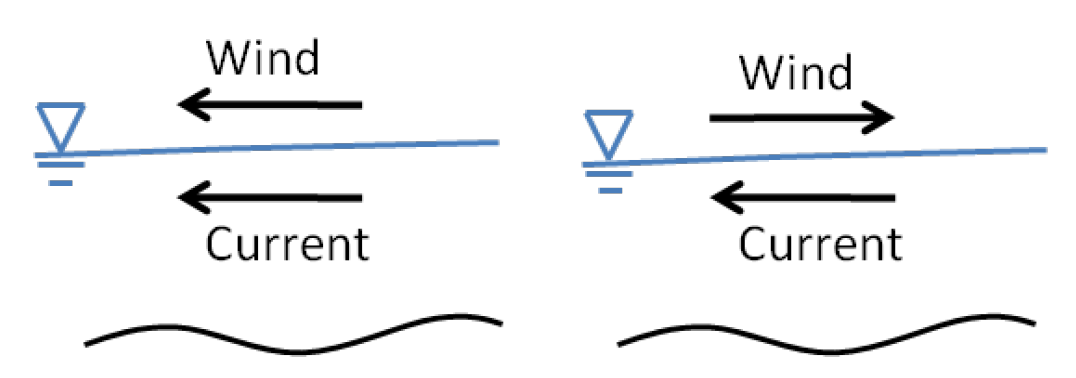

Schematic of wind and currents in same (left) and opposing directions (right).

Drag Coefficient

There are a wide variety of drag coefficient formulas in literature. Within HEC-RAS, four drag coefficient formulations are available for use that provide a reasonable range of options.

The Hsu (1988) formula is written as:

3)	$\begin{array}{l}\displaystyle \displaystyle C_D = \left( \frac{\kappa}{14.56 -2 ln W_{10}} \right) ^2\end{array}$

where $\begin{array}{l}W_{10} = \left| \textbf{W} _{10} \right|\end{array}$ is the 10-m wind speed [m/s]. The Hsu formula was developed by assuming a logarithmic wind velocity profile and substituting an expression for the aerodynamic roughness length based on fully developed ocean waves. Several linear formulas have been proposed in literature for the drag coefficient. Here two are implemented and available in HEC-RAS. Garratt (1977) proposed:

4)	$\begin{array}{l}\displaystyle \displaystyle C_D = 0.001(0.75 + 0.067 W_{10})\end{array}$

Large and Pond (1981) proposed a similar expression:

5)	$\begin{array}{l}\displaystyle \displaystyle C_D = 0.001(0.49+0.065W_{10})\end{array}$

In HEC-RAS the Garrat (1977) and Large and Pond (1981) methods are limited within the range of 0.75x10^-3 and 2.64x10^-3.

Andreas et al. (2012) utilized almost 7,000 measurements over the sea to fit an empirical expression for the water surface shear velocity, which is applicable to both smooth and rough turbulent flow:

6)	$\begin{array}{l}\displaystyle \displaystyle w_* = 0.239+0.0433 \left\{ (W_{10} - 8.271)+ \left[ 0.120 (W_{10} -8.271)^2+0.181 \right] ^{1/2} \right\}\end{array}$

where $\begin{array}{l}w_*\end{array}$ = wind shear velocity [m/s]. The drag coefficient is then calculated as:

7)	$\begin{array}{l}\displaystyle \displaystyle C_D = \left( \frac{w_*}{W_{10}} \right) ^2\end{array}$

A comparison of the four wind drag coefficient formulations is provided in the figure below. The four methods differ significantly at weak wind speeds but especially strong wind speeds. For strong wind speeds above 30 m/s, only the Andreas et al. (2012) method is recommended, since it is the only method which has been compared to measurements at high wind speeds. The other methods were not calibrated for high wind speeds.

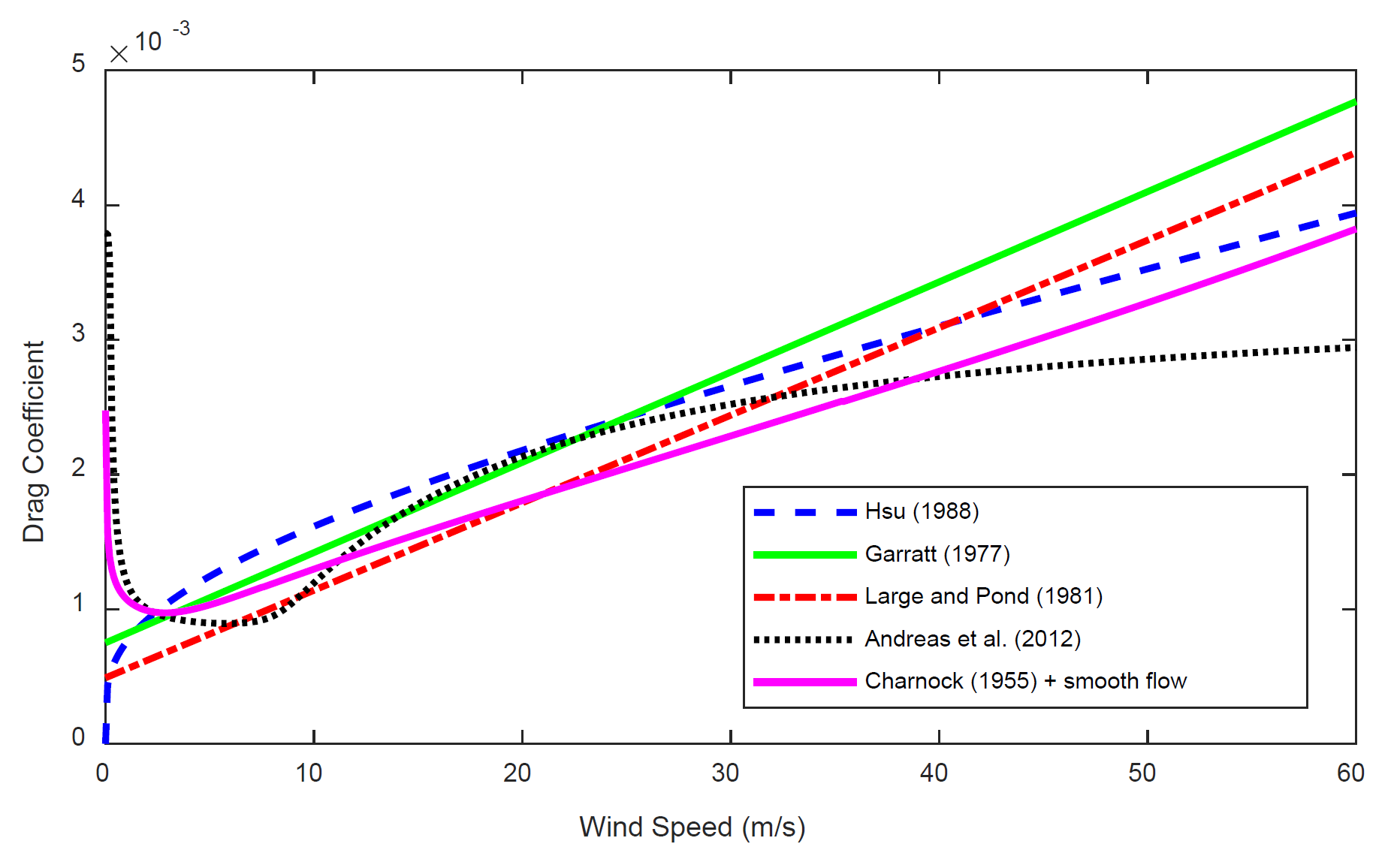Wind drag coefficient. Figure 1. Comparison of four wind drag coefficient formulations.

It is important to mention that each of the expressions were derived assuming fully developed sea states. That is, they do not consider the wind/wave variables such as wave height and period or swell direction and height. More importantly, for fetch limited water bodies, such as reservoirs and rivers, the above expressions may overestimate the drag coefficient.

Wind Ratio

The wind ratio is directly multiplied by the input wind velocities. It may be used to scale the wind, to convert the input wind velocity units, or to convert between different wind velocity definitions. Wind measurements are usually obtained as mean or “maximum sustained” wind in a certain time period. Generally, for hydrodynamic modeling, mean wind speeds should be used (e.g., 10-min or 30-min averages). Maximum sustained winds, may be converted to mean values using the wind ratio.