The downstream cross section is a mandatory hydraulic model boundary location, so the Quasi-Unsteady flow editor automatically populates a row for the downstream cross section. HEC-RAS has three quasi-unsteady, downstream boundary conditions.

Stage Time Series

Quasi-unsteady flow has three downstream boundary conditions, all specifying downstream stages for each steady flow backwater computation. If stage data are available or projected for the simulation period, the Stage Time Series can set the downstream boundary (below).

This editor follows the standard irregular time series format of a duration associated with a stage. No computation increment is required for a Stage Time Series.

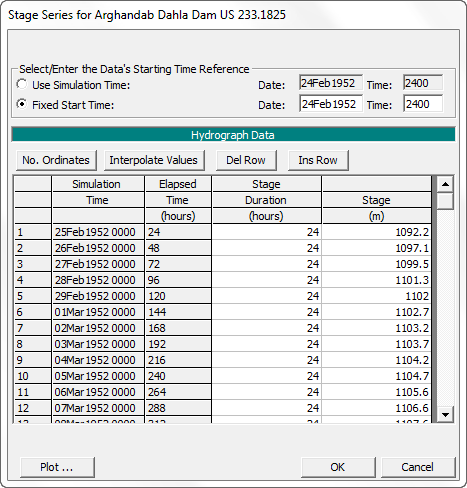
The stage time series is usually the best option for historical analysis. When using this feature for to predict future time series, however, be careful to set it at a reach in morphological quasi-equilibrium (e.g. a reach that is not actively aggrading or degrading on the decadal time scale).

Rating Curve

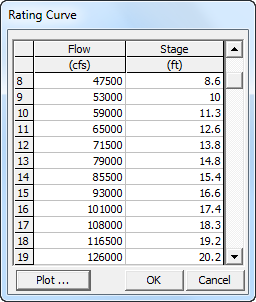
In the absence of time series data, a rating curve can define a downstream relationship between stage and flow, computing downstream boundary stages in response to the simulation flow series. The Rating Curve button launches a dialogue where users can enter a flow-stage rating curve for the downstream cross section (below). Be careful to place flow and stage in the correct columns (they are inverted from other editors). HEC-RAS will interpolate a boundary stage from the rating curve for each time step based on the flow. Like the stage time series, applying a rating curve boundary condition to predictive analyses assumes the downstream boundary condition is essentially in morphological quasi-equilibrium (i.e. not expecting long term deposition or erosion trends).

Normal Depth

The final downstream boundary option is Normal depth. The Normal Depth button launches a simple window requesting a single parameter: the Friction Slope. The friction slope (S_f in Manning's equation) is the slope of the energy grade line and can be estimated a prior by measuring the slope of the bed (press the Alt key in the HEC-RAS Water Surface Profile output view to get a tool that will measure the slope). With the friction slope, the flow, the n-value and the cross-section shape specified, HEC-RAS can back-calculate stage from Manning's Equation.

Modeling Note: Downstream Boundary Condition – Depth vs. Stage

Normal Depth is a popular boundary condition in steady and unsteady flow because it requires so little data. However, it also introduces more uncertainty than the stage series or the rating curve options. It is also popular in quasi-unsteady sediment analysis, for the same reasons. However Normal Depth can introduce troubling numerical feedback in the sediment model in addition to hydraulic uncertainties and should be used with caution.

Setting a downstream depth rather than stage, makes the water surface elevation independent of the computed channel elevation. There is no feedback between bed change and water surface elevation. For stage boundary conditions, if the bed aggrades, shear will increase, and the rate of aggradation will drop until the cross-section approaches equilibrium. Erosion will introduce the opposite feedback, settling similarly on an equilibrium geometry. Therefore, stage boundary conditions should be specified in quasi-equilibrium reaches.

A depth boundary condition will continue to aggrade or degrade without water surface feedbacks. The next time step will simply compute a new depth on the new cross section shape. This can introduce numerical artifacts, where normal depth boundary conditions aggrade or degrade unrealistically over the simulation. Therefore, while convenient, normal depth is often a poorly posed boundary condition for sediment transport models, unless the downstream cross section is in equilibrium. The user can force equilibrium by setting the downstream boundary condition as a Pass Through Node, however, this sometimes just pushes the numerical problem one cross section upstream.