Download PDF
Download page Vertical Mixing.
Vertical Mixing
Three methods are available in HEC-ResSim to estimate reservoir vertical diffusion coefficients (D_z).
Stability Method
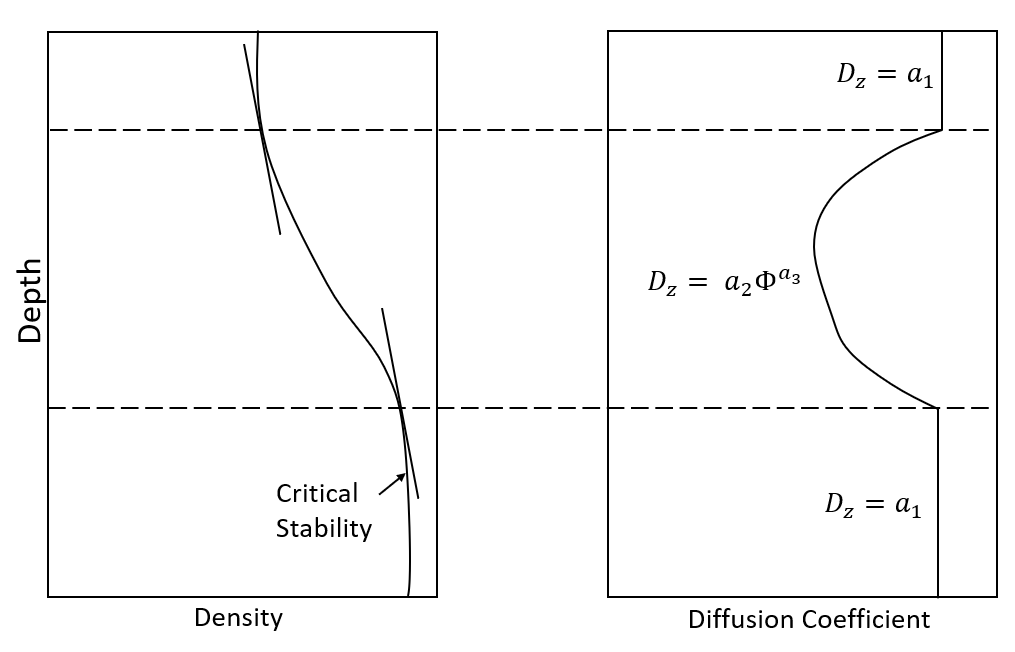
The stability method calculates diffusion coefficients as a function of the water column stability (\Phi). Stability is defined by the reservoir's normalized vertical density gradient.
| \Phi = \frac{1}{\rho} \frac{\partial\rho}{\partial z} |
A minimum water column stability \Phi_{\textrm{crit}} is defined by the user (default value 0.2×10-6 1/m). Below this value, the water column is considered well-mixed and the diffusion coefficient is set at a maximum value. Above, density stratification limits mixing, and the diffusion coefficients are calculated using a power law relationship.
| \[ D_z = \begin{cases} a_1 & \quad \textrm{if } \Phi \leq \Phi_{\textrm{crit}}\\ a_2 \Phi^{a_3} & \quad \textrm{otherwise} \end{cases} \] |
where
a_1 is a user-defined maximum vertical diffusion coefficient [m2/s],
a_2 is an empirical constant, calculated to ensure a continuous function at the point E = E_{\textrm{crit}} [m2/s], and
a_3 is an empirical constant [unitless, default value 0.7].
A density profile and the resulting diffusion coefficients for this method are shown below.
Wind Method
The wind method estimates reservoir vertical diffusion coefficients as a function of wind speed and depth relative to the thermocline.
| D_z = D_{z,\textrm{min}} + a_1 \, U_{\textrm{wind}} \, \textrm{exp}\left( -a_2 \frac{d_i}{d_\textrm{therm}} \right)} |
where
D_{z,\textrm{min}} is a user-entered minimum vertical diffusion coefficient [m2/s],
a_1 is an empirical constant (default value ),
U_{\textrm{wind}} is the wind speed measured at (default value ),
a_2 is an empirical constant (default value ),
d_i is the depth of reservoir layer i [m], and
d_{\textrm{therm}} is the depth of the thermocline [m].
Munk and Anderson Method
| D_z = \textrm{max} \left(D_{z,\textrm{min}} \frac{D_{z,\textrm{max}}}{\left(1+aR_i\right)^b} \right) |
where
D_{z,\textrm{min}} is a user-entered minimum vertical diffusion coefficient [m2/s],
D_{z,\textrm{max}} = c \omega_{\theta} is the maximum vertical diffusion coefficient [m2/s],
\omega_{\theta} = \sqrt{\tau_s / \rho} is the wind shear velocity [m/s],
\tau_s is the wind induced shear stress at the water surface [],
\rho is the density of the surface water [kg/m3],
R_i is the Richardson number [unitless], and
a, b, c are empirical coefficients.
The Richardson number quantifies the opposing influences of wind-induced shear stress, which drives vertical mixing, and water column stability, which inhibits mixing.
| R_i = \frac{\frac{g}{\rho}\frac{\partial \rho}{\partial z}}{\omega^2_{\theta}/(\eta-z)^2} |
where
g is gravitational accelaration,
\eta is the water surface elevation [m], and
z is the elevation where D_z is computed [m].
Additional Mixing
Separate logic is required in reservoir simulations in order to mix vertical layers and achieve stable stratification profiles. Stable stratification profiles are required for the correct functioning of the inflow and outflow allocation routines. Unstable profiles may result from convective cooling at the reservoir surface layer. In a physical reservoir, this instability would result in "penetrative convection" which would physically mix the layers. In the water quality engine, the same approach is taken as is used in HEC-5Q, whereby a filter is applied following the solution to the constituent transport equation. Starting from the water surface, the density of the current layer is checked against the density of the layer immediately below it. If an instability is present, the layers are mixed by redistributing the constituent masses to achieve equal concentrations in both layers. The process is repeated, mixing more total layers, until a stable density profile is achieved.
Additional sources of energy (other than penetrative convection) act to mix layers in a reservoir. These include (Fisher, et al.)
- mixing from momentum transfer of wind energy at the water surface
- inflow and outflow mixing
- mixing of internal layers due to seiching
Future development of the water quality engine may take these sources of mixing into account.