Nutrient Simulation Module I

The Nutrient Simulation Module I (NSMI) is capable of simulating algae, nutrient, and oxygen cycling. NSMI can model up to 15 water quality constituents (state variables) in the water column, as listed in List of water quality state variables included in NSMI. This module allows users to selectively activate or deactivate any state variable, providing flexibility in its application. When a state variable is activated (on), NSMI computes associated pathway fluxes, when deactivated (off), no pathway fluxes are computed for that variable. If a state variable is bypassed, the user does not need to provide input parameters, boundary conditions, or initial conditions. However, the water quality model results may not be reasonable when some of these state variables are deactivated due to interactions among them. Therefore, care must be taken when turning off these state variables.

Concentrations of constituents are expressed in milligrams per liter (mg L^-1). Symbols abbreviated as Chl, D, C, N, P and O₂ refer to the weights of chlorophyll-a, dry biomass, carbon, nitrogen, phosphorus, and oxygen, respectively.

 List of water quality state variables included in NSMI.

Schematic of the state variables and kinetic processes in NSMI provides an overview of the state variables and processes modeled by NSMI. Aquatic plants are divided into two broad categories: (1) those that move freely with water (floating algae) and (2) those that remain fixed or attached to the bottom (benthic algae). Both forms of algae are included in NSMI. Organic nitrogen, phosphorous and carbon are simulated as a single type of detrital organic matter, each with different parameters for decomposition and settling. In NSMI, Alkalinity (Alk) and Pathogen (PX) do not affect the other water quality state variables in the water column. Carbonaceous Biological Oxygen Demand (CBOD) impacts dissolved oxygen (DO), while the remaining water quality state variables interact with one another.

Schematic of the state variables and kinetic processes in NSMI

Algae

In NSMI, algae encompass microscopic phytoplankton, free-floating weeds, and certain types of other plants.  Algal biomass is computed in µg-Chl L^-1 of phytoplankton. The net change in algal biomass at each time step is calculated as the difference between the increase due to primary production and the losses from respiration, mortality, and sedimentation. Photosynthesis is the process by which algae use sunlight to convert carbon dioxide (CO₂) into a food source while releasing oxygen as a by-product. Respiration, the reverse of photosynthesis, indicates that the products of photosynthesis become the reactants in respiration, and vice-versa. Since photosynthesis requires light, it occurs only during daylight hours, while respiration occurs continuously, 24 hours a day. Algal mortality produces organic matter that eventually decays, further consuming DO. Both algal respiration and decomposition contribute to high oxygen demands. The kinetic source (+) and sink (-) rate equation for algal biomass in the water column is expressed as:

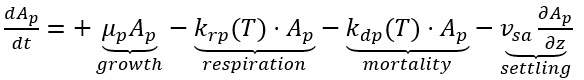                                    (23)

where

           A_p = algae (µg-Chl L^-1)

           m_p = algal growth rate (d^-1)

       k_rp(T) = algal respiration rate (d^-1)

       k_dp(T) = algal mortality rate (d^-1)

           v_sa = algal settling velocity (m d^-1).

Chlorophyll-a represents the total concentration of chlorophyll-a, expressed in units of µg-Chl L^-1 or mg-Chl m^-3. To obtain algal biomass, the chlorophyll-a concentration is multiplied by r_da (D:Chl ratio).

                                                                                                       (24)

where

           r_da = D:Chl ratio for algae (mg-D µg-Chl^-1)

          A_pd = algal biomass (dry weight) (mg-D L^-1).

In the model, r_da is a fixed value; however, in a natural setting, this rate is not constant and varies based on light and nutrient availability.

Factors that limit the growth and abundance of algae include light, temperature, nutrients, and discharge. Like other water quality models, the algal growth rate is calculated based on the maximum growth rate under optimal conditions of temperature, light and nutrients. This maximum growth rate is then adjusted using temperature, light intensity, and a single limiting nutrient under ambient conditions (Kiffney and Bull 2000, Weckstrom and Korhola 2001, Cascallar et al. 2003). NSMI includes three options for calculating the algal growth rate: (1) multiplicative; (2) limiting nutrient; and (3) harmonic mean.

(1) Multiplicative option

This option has its biological basis in the multiplicative effects of the enzymatic processes involved in photosynthesis. The multiplicative formulation combines the growth limiting factors for light, nitrogen, and phosphorus to determine their net effect on the local algal growth rate. Each of these factors operates independently, and under optimal conditions, each limiting factor is assigned a value of one. When conditions are not optimal, these factors are given fractional values.

                                                                                   (25)

where

      m_mxp(T) = maximum algal growth rate (d^-1)

          FL = light limiting factor for algal growth (0–1.0)

          FN = N limiting factor for algal growth (0–1.0)

          FP = P limiting factor for algal growth (0–1.0).

(2) Nutrient limiting option

This approach reflects Liebig’s law of the minimum. The nutrient-limiting formulation calculates  an algal growth rate that is constrained by light and either nitrogen or phosphorus. While the effects of nutrient and light effects are multiplicative, the nutrient effects serve as an alternative to using the smaller limiting factors.

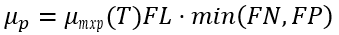                                                                    (26)

(3) Harmonic mean option

The harmonic mean is mathematically analogous to the total resistance of two resistors in parallel, serving as a compromise between the previous two options. In this formulation, the algal growth rate is governed by a multiplicative relationship between light and nutrients, while nutrient limitations are represented using the harmonic mean.

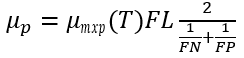                                                                                        (27)

The light limiting factor for algal growth is calculated based on photosynthetically active radiation (PAR) intensity. Photosynthesis occurs at varying depths throughout the water column. Light attenuation is simulated as an exponential decrease in light intensity with depth, following the Beer-Lambert law. NSMI includes three light functions: (1) Half-saturation function (Baly 1935), (2) Smith’s function (Smith 1936), and (3) Steele’s function (Steele 1962).

(1) Half-saturation light function

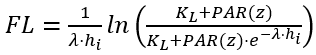                                                                        (28)

(2) Smith’s light function

                                           (29)

(3) Steele’s light function

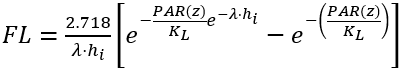                                           (30)

and

                                                                                              (31)

where

    PAR(Z) = PAR at depth z below the water surface (W m^-2)

             λ = light attenuation coefficient (m^-1)

            h_i = thickness of layer i (m)

           K_L =  light limiting constant for the algal growth (W m^-2).

The light attenuation (also called extinction) rate describes the decrease in light intensity with depth in the water column. It is calculated as the sum of several partial attenuation coefficients, which depend on the concentration of suspended solids and their optical properties. This includes the baseline attenuation rate for water, self-shading by plants, and attenuation due to suspended sediment, particulate organic matter, and algae. In NSMI, the light attenuation coefficient is estimated by:

                                                   (32)

where

            λ₀ = background light attenuation (m^-1)

            λ_s = light attenuation by inorganic suspended solids (L mg^-1 m^-1)

           λ_m = light attenuation by organic matter (L mg^-1 m^-1)

            λ₁  = linear light attenuation by algae (m^-1 (µg-Chl L^-1)^-1)

            λ₂  = nonlinear light attenuation by algae (m^-1 (µg-Chl L^-1)^-2/3)

      POM = particulate organic matter (mg-D L^-1)

           m_n = inorganic suspended solid “n” (mg L^-1).

The baseline attenuation accounts for light reduction due to color and other factors not related to suspended solids and algae. The impact of organic matter on the light attenuation is considered based on the concentration of particulate organic carbon (POC) in the water column. In the equation above, m_n does not include organic material. If the values for suspended solids have been adjusted to include both organic and inorganic materials in the water column, the default values of λ_s and λ_m must also be modified. The percentages of organic and inorganic material in water-quality samples are determined using various methodologies (APHA 1992).

The half-saturation function is commonly used to assess nutrient limitation and primary productivity in aquatic systems. This function relates the growth rates of aquatic plants and algae to the availability of dissolved nutrients. In NSMI, the half-saturation function is evaluated for both inorganic nitrogen and phosphorous, with the minimum value chosen to adjust the algal growth rate. Carbon is typically available in excess, so carbon limitation is not included as a  nutrient limiting factor. The limiting factor for the effect of nitrogen on the algal growth rate is calculated by:

                                                                                                   (33)

Similarly, the limiting factor for the effect of phosphorus on the algal growth rate is calculated by:

                                                                                                                      (34)

where

       NH4 = ammonium (mg-N L^-1)

       NO3 = nitrate (mg-N L^-1)

         DIP = dissolved inorganic phosphorous (mg-P L^-1)

           K_sN = half-saturation N constant for algal growth (mg-N L^-1)

           K_sP = half-saturation P constant for algal growth (mg-P L^-1).

Algal respiration is the reverse of the photosynthesis process and contributes to the reduction in the phytoplankton biomass. If the respiration rate of phytoplankton exceeds the growth rate, there is a net loss of phytoplankton carbon or biomass.

Algal mortality is divided among detritus, sediment, and labile dissolved organic matter. By appropriately choosing coefficients, calculated values for all terms can be zero. This mortality rate encompasses both natural and predator mortality.

The net settling rate of algae can be negative. If the settling velocity is positive, settled algae serve as a source for the layer below. If the settling velocity is negative, the settling term of algae for a given layer represents a loss.

Benthic Algae

The term periphyton is sometimes used to refer to benthic algae and at other times to the entire community of attached microorganism, including algae, bacteria, fungi, and protozoa. To avoid confusion, benthic algae are used in NSMI to designate the algal community attached to the substrate. The amount of benthic algae is expressed in terms of density per unit bottom area (g-D m^-2).  Factors that control benthic algae biomass include light, temperature, current, substrate type, scouring from high discharge, water chemistry, and grazing by invertebrates. Benthic algae biomass is computed by solving the following kinetic source (+) and sink (-) rate equations.

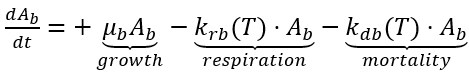                                                                       (35)

where

           A_b = benthic algae (g-D m^-2)

           m_b = benthic algae growth rate (d^-1)

      k_rb(T) = benthic algae base respiration rate (d^-1)

       k_db(T) = benthic algae mortality rate (d^-1).

Benthic algae biomass is converted to the areal concentration of chlorophyll-a using the following equation:

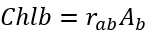                                                                                                                                               (36)

where

           r_ab = Chl:D ratio for benthic algae (µg-Chl mg-D^-1)

       Chlb = benthic chlorophyll-a (mg-Chl m^-2).

Respiration is the reverse of the photosynthesis process, and the mortality rate accounts for both natural and predator -related mortality. Both respiration and mortality are simulated using first-order kinetics.

The growth of benthic algae depends on the availability of certain limiting resources, including light intensity, nutrients, and bottom area density (space). These factors are simulated as limiting conditions that attenuate the maximum growth rate. Two sets of options are provided for calculating benthic algae growth: (1) multiplicative and (2) nutrient limiting. These options are similar to those used for algae, with the exception of the effect of space limitation on benthic algae growth.

(1) Multiplicative option

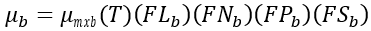                                                                    (37)

where

     m_mxb(T) = maximum benthic algae growth rate (d^-1)

         FL_b = light limiting factor for benthic algae growth (0–1.0)

        FN_b = N limiting factor for benthic algae growth (0–1.0)

         FP_b = P limiting factor for benthic algae growth (0–1.0)

         FS_b =  bottom area limiting factor for benthic algae growth (0–1.0).

(2) Nutrient limiting option

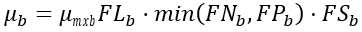                                                                     (38)

The temperature limiting factor is calculated using Arrhenius Equation. Light limiting factor is calculated using three optional functions. The light limiting factor for benthic algae growth is determined by the amount of PAR reaching the bottom of the water column. Three sets of functions are included to calculate the light limiting factor for benthic algae growth: (1) half-saturation, (2) Smith, and (3) Steele.

(1) Half-saturation function

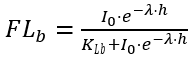                                                                                                              (39)

(2) Smith’s function

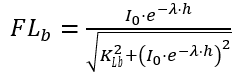                                                                                                     (40)

(3) Steele’s function

                                                                                             (41)

where

           K_Lb = light limiting constant for benthic algae growth (W m^-2).

Nutrient limitation depends on the concentrations of nitrogen and phosphorus in aquatic environments. Nitrogen and phosphorus limiting factors for benthic algae growth are calculated similarly to those for algae growth, with the exception that the user can supply different half-saturation constants for nitrogen and phosphorous specific to benthic algae.

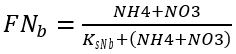                                                                                                 (42a)

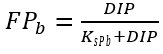                                                                                                                 (42b)

where

          K_sNb  = half-saturation N constant for benthic algae growth, (mg-N L^-1)

          K_sPb = half-saturation P constant for benthic algae growth (mg-P L^-1).

Benthic algae growth is further limited by the availability of substrate, which includes the littoral bottom and the available bottom area. Attached algae typically exhibit lateral heterogeneity, with higher densities observed at shallower depths. A half-saturation function is employed to attenuate the growth rate of benthic algae as their density on the bottom increases.

                                                                                                (43)

where

          K_Sb  = half-saturation density constant for benthic algae growth (g-D m^-2).

Nitrogen Constituents

In NSMI, the nitrogen cycle simulates the transformations of organic nitrogen (OrgN), ammonium (NH4), nitrite (NO2), and nitrate (NO3). In aerobic water, there is a stepwise transformation from OrgN to NH4, to NO2, and, finally, to NO3. The release of nutrients from sediments may also be significant, occurring as a result of a concentration gradient between the water column and the nutrient-rich pore water in the sediment. Algae uptake and release nutrients, and when they die, hydrolytic bacteria quickly recycle these nutrients into their respective compartments.

Particulate and aqueous fractions of organic nitrogen in the water column are combined as a single state variable. OrgN is produced as algae die and is lost due to decay and settling. The production of OrgN from  algae death is calculated using a stoichiometric ratio that represents the fraction of nitrogen content. The kinetic source (+) and sink (-) rate equation for the concentration of OrgN in the water column is expressed as:

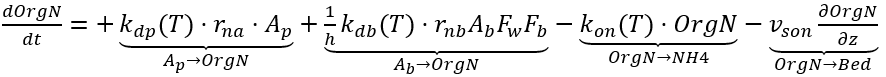       (44)

where

      OrgN = organic nitrogen (mg-N L^-1)

           r_na = N:Chl ratio for algae (mg-N µg-Chl^-1)

       k_on(T) = decay rate of organic N into NH4 (d^-1)

           v_son = organic N settling velocity (m d^-1)

           r_nb = N :D ratio for benthic algae (mg-N mg-D^-1)

           F_w = fraction of benthic algae mortality into the water column (0–1.0)

           F_b = fraction of bottom area available for benthic algae growth (0–1.0).

Sources of NH4 in the water column include the decay of organic nitrogen and releases from algal respiration and bottom sediments. Nitrification consumes oxygen and represents a loss process for NH4. The kinetic source (+) and sink (-) rate equation for the concentration of NH4 in the water column is expressed as:

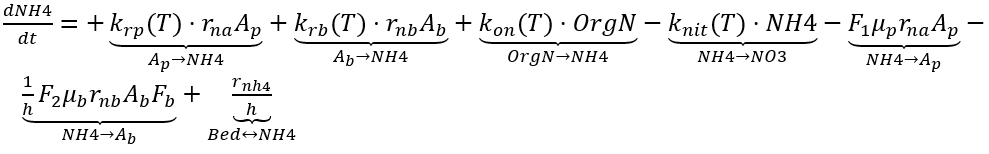      (45)

where

       k_nit (T)   = nitrification rate of NH4 to NO3 (d^-1)

           r_nh4   = sediment release rate of NH4 (g-N m^-2 d^-1)

           F₁ = preference fraction of algal uptake from NH4 (0–1.0)

           F₂  = preference fraction of benthic algae uptake from NH4 (0–1.0).

Nitrogen uptake rate is based on the fraction of NH4 available compared to NO3. For physiological reasons, the preferred form for algal uptake is NH4. The preference fractions of algae and benthic algae uptake from the water column NH4 are calculated using the following equations:

                                                                                     (46a)

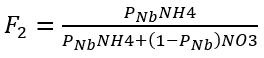                                                                                      (46b)

where

           P_N = NH4 preference factor for algal growth,

         P_Nb = NH4 preference factor for benthic algae growth.

The process of nitrification occurs in a two-step process. During nitrification, NH4 is oxidized first to NO2, and then to NO3. The nitrification rate decreases at low levels of DO, which can be adjusted using the inhibition correction factor (Brown and Barnwell 1987):

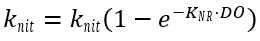                                                                                     (47)

where

          K_NR   = oxygen inhibition factor for nitrification (0.6 – 0.7) (mg-O₂ L^-1).

Nitrite in the water column is combined with nitrate, as it typically exists in much smaller quantities. The combined concentration of nitrate and nitrite is simulated as a state variable referred to as NO3. NO3 is formed through nitrification and removed via denitrification. Denitrifying bacteria thrive in the anaerobic surface layer of the sediment (Kusuda et al. 1994). Pauer and Auer (2000) noted that denitrification is generally a sediment-based phenomena rather than one occurring in the water column. However, denitrification can also take place in the water column where NO3 is present but oxygen is limited (Di Toro 2001). Optimum conditions for denitrification include high NO3 levels, sufficient degradable organic material, low DO, and elevated temperature. Denitrification is limited by the availability of NO3 and is inhibited by DO. Following the convention of other water quality models, denitrification in the water column is also included in NSMI. NO3 is consumed during photosynthesis.

The kinetic source (+) and sink (-) rate equation for the concentration of NO3 in the water column is expressed as:

         (48)

where

      k_dnit(T) = denitrification rate (d^-1)

        K_sOxdn = half-saturation oxygen constant for denitrification (mg-O₂ L^-1)

           v_no3 = sediment denitrification velocity (m d^-1).

Because organic nitrogen is a byproduct of algae, modeled organic nitrogen needs to be adjusted for algal composition and compared to total organic nitrogen (TON) measurements. Measured TON includes organic nitrogen along with the nitrogen incorporated into algal biomass. To facilitate comparison with measured TON, algal organic nitrogen is added to OrgN. The concentrations of Dissolved Inorganic Nitrogen (DIN), Total Organic Nitrogen (TON), Total Kjeldahl Nitrogen (TKN), Total Nitrogen (TN) in the water column are directly calculated from modeled state variables as follows.

                                                                                         (49a)

                                                                                     (49b)

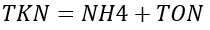                                                                                        (49c)

                                                                                             (49d)

where

        DIN = dissolved inorganic nitrogen (mg-N L^-1)

       TON = total organic nitrogen (mg-N L^-1)

       TKN = total Kjeldahl nitrogen (mg-N L^-1)

         TN = total nitrogen (mg-N L^-1).

Phosphorus Constituents

The phosphorus cycle is simpler than the nitrogen cycle. In NSMI, organic phosphorus, as well as dissolved and particulate inorganic phosphorus, are modeled. A key reaction in the phosphorus cycle is the adsorption and desorption of inorganic phosphorus. Inorganic phosphorus can exist in both dissolved forms and as adsorbed onto suspended sediment particles. Both algae and benthic algae are linked to the phosphorus cycle through the processes of growth, respiration, and death.

Organic phosphorus (OrgP), which includes both particulate and dissolved components in the water column, is simulated as a single state variable. OrgP is produced by both algae and benthic algae and is lost through mineralization and settling. The production of organic phosphorus from algal death is calculated using a stoichiometric ratio that represents the fraction of phosphorus content. The kinetic source (+) and sink (-) rate equation for the concentration of OrgP in the water column is expressed as:

            (50)

where

      OrgP = organic phosphorous (mg-P L^-1)

           r_pa   = P:Chl ratio for algae (mg-P µg-Chl^-1)

       k_op(T) = decay rate of organic P into DIP (d^-1)

           v_sop = organic P settling velocity (m d^-1)

           r_pb   = P:D ratio for benthic algae (mg-P mg-D^-1).

To compare modeled organic phosphorus to total organic phosphorus (TOP) measurements, it must be corrected for algal composition. Measured TOP includes organic phosphorus and the phosphorus incorporated into algal biomass. he phosphorus content from algae is added to the modeled OrgP for comparison with the measured TOP.

In NSMI, Total Inorganic Phosphorus (TIP) is included as a single state variable. In the water column, inorganic phosphorous serves as one of the primary nutrients for aquatic plants. In water quality reporting, inorganic phosphorous is typically referred to as Dissolved Inorganic Phosphorus (DIP) or by the technical term Filterable Reactive Phosphorus (FRP). Inorganic phosphorus is strongly adsorbed to solid particles, especially fine-grained, cohesive particles (e.g., clay, silt, organic matter), rendering it less available as a nutrient (Tate et al. 1995). Inorganic phosphorous is lost through uptake during algal growth and solids settling, when it is gained from sediment release and the decay of organic phosphorus. The kinetic source (+) and sink (-) rate equation for the concentration of TIP in the water column is expressed as:

         (51)

where

         TIP = total inorganic phosphorus (mg-P L^-1)

           v_sp = settling velocity of suspended sediments (m d^-1)

           r_po4 = sediment release rate of DIP (g-P m^-2 d^-1).

McGechan and Lewis (2002) present the empirical equations commonly used to represent phosphorus adsorption and desorption in soils. These equations are often adapted for use in water quality models, with modifications to account for factors such as pH, DO, and the concentrations of sediment aluminum and iron. In NSMI, the distribution of inorganic phosphorus between the aqueous and particulate phases is calculated using a linear sorption isotherm. The partitioning fractions of the inorganic phosphorus are determined as a function of the partition coefficients and the concentrations of solids.

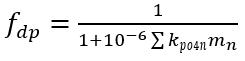                                                                                                                                        (52a)

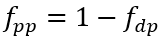                                                                                                                                                        (52b)

where

           f_dp   = dissolved fraction of inorganic P (0–1.0)

           f_pp   = particulate fraction of inorganic P (0–1.0)

         k_dpo4n = partition coefficient of inorganic P for solid “n” (L kg^-1).

The partitioning distribution coefficient (k_dpo4) is defined as the ratio of concentration of inorganic phosphorous adsorbed onto solids (mass chemical per mass solids) to the concentration of inorganic phosphorous dissolved in water, with units of L kg^-1. A wide range of partition coefficients for phosphate has been reported in the literature and also treated as a calibration parameter.

The concentrations of DIP, Total Organic Phosphorus (TOP), Total Phosphorus (TP) in the water column are directly computed from the modeled state variables as follows.

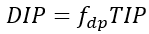                                                                                                                                                       (53a)

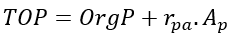                                                                                                                                 (53b)

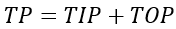                                                                                                                                                     (53c)

where

        TOP = total organic phosphorus (mg-P L^-1)

           TP = total phosphorus (mg-P L^-1).

As discussed previously for TON, algal phosphorous is included in the total organic phosphorous in Eq. 28b.

Carbon Constituents

In NSMI, organic carbon is divided into two fractions: particulate organic carbon (POC) and dissolved organic carbon (DOC). Both POC and DOC are primary products of aquatic primary production. POC represents non-living particulate detrital carbon, while DOC is the portion of total organic carbon (TOC) that is dissolved in water, in contrast to the portion that remains in suspension. Additionally, carbonaceous biochemical oxygen demand (CBOD), often expressed as O₂, is typically measured and reported in water quality data. NSMI models aquatic carbon cycle using four state variables: POC, DOC and dissolved inorganic carbon (DIC), and CBOD.

The behavior, reactivity, and fate of organic carbon in the water column strongly depend on whether it is present in dissolved or particulate phases. The only source of POC is algal contribution, and algal mortality is partitioned between POC and DOC. The kinetic source (+) and sink (-) rate equation for the concentration of POC in the water column is stated as:

           (54)

where

       POC = particulate organic carbon (mg-C L^-1)

       F_pocp = fraction of algal mortality into POC (0–1.0)

           r_ca = C:Chl ratio for algae (mg-C µg-Chl^-1)

           r_cb = C:D ratio for benthic algae (mg-C mg-D^-1)

           v_soc = POC settling velocity (m d^-1)

       k_poc(T) = POC hydrolysis rate (d^-1)

       F_pocb = fraction of benthic algae mortality into POC (0–1.0).

Significant components of DOC in water primarily originate from autochthonous production by algae and plant communities. Additionally, sediments can serve as an important source of DOC in the water column. The flux of pore-water DOC across the sediment–water interface has been shown to contribute significantly to the total DOC in estuaries (Burdige 2001, 2002; Maher and Eyre 2011). DOC oxidation occurs aerobically and is therefore reduced at low DO concentrations. Under these low DO conditions, the denitrification reaction consumes DOC. The kinetic source (+) and sink (-) rate equation for the concentration of DOC in the water column is expressed as:

     (55)

where

        K_sOxmc = half saturation oxygen constant for DOC oxidation rate (mg-O₂ L^-1)

      k_doc(T) = DOC oxidation rate (d^-1)

           f_com = fraction of carbon in organic matter (mg-C mg-D^-1).

Inorganic carbon constituents in waters include carbon dioxide (CO₂), bicarbonate (HCO₃^-), and carbonate (CO₃^2-). The sum of these constituents is referred to as Dissolved Inorganic Carbon (DIC).

                                                                (56)

where

        DIC = dissolved inorganic carbon (mol L^-1)

H2CO3* = sum of dissolved CO₂ and carbonic acid (mol L^-1)

    HCO₃^- = bicarbonate ion (mol L^-1)

     CO3^2- = carbonate ion (mol L^-1).

The proportions of the various ionic forms of DIC - H₂CO₃, HCO₃^-, CO₃^2- are largely controlled by pH. HCO₃^- is typically the dominant component of DIC in natural waters, especially when pH ranges between 6.35 and 10.33 with HCO₃^- being the most abundant form at pH 6-8. In contrast,  CO₂ and H₂CO₃ predominate at lower pH levels.

DIC is produced through decomposition and is assimilated by plants; it is also a by-product of respiration in aquatic plants. Additional sources and sinks of DIC arise from exchanges with the atmosphere and the oxidation of organic carbon (i.e., DOC, CBOD). DIC is modeled in units of mole or mol L^-1, where 1 mole of DIC is equal to 12 gram, and 1 mol L^-1 = 12000 mg-C L^-1.

The kinetic source (+) and sink (-) rate equation for the concentration of DIC in the water column is expressed as:

                                                                                                                                                                                                           (57)

where

      k_ac(T) = CO₂ reaeration rate (d^-1)

      K_H(T) =  Henry’s Law constant of CO₂ (mol L^-1 atm^-1)

          p_CO2  =  partial pressure of CO₂ in the atmosphere (ppm)

          F_CO2 = fraction of total inorganic carbon in CO₂ (0–1.0).

Atmospheric reaeration of CO₂ refers to the transfer of CO₂ across the air–water interface. The rate of CO₂ reaeration is proportional to the difference between CO₂ saturation and the actual dissolved CO₂ concentration. CO₂ saturation is primarily determined by the partial atmospheric CO₂ pressure (P_CO2) and water temperature.

The Henry’s Law constant (K_H) varies for each gas, temperature, and solvent. For CO₂, the K_H is calculated as a function of water temperature given by Edmond and Gieskes (1970).

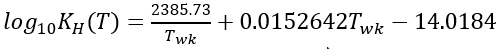                                                        (58)

where

          T_wk = water temperature in Kelvin.

The reaeration rate for CO₂ is derived from the oxygen reaeration rate using the following relationship.

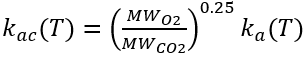                                                                                           (59)

where

        k_a(T) = oxygen reaeration rate (d^-1)

       MW_O2 = molecular weight of O₂ (= 32 g mol^-1)

     MW_CO2 = molecular weight of CO₂ (= 44 g mol^-1).

CBOD directly impacts the amount of dissolved oxygen in water bodies, with a positive correlation between CBOD and oxygen depletion. CBOD is subject to oxidation loss and removal through processes such as sedimentation, scour and flocculation, which exert an oxygen demand as described in QUAL2E (Brown and Barnwell 1987). The CBOD oxidation ceases if the water becomes anaerobic. Notably, the algal contribution to CBOD is not included in NSMI. The kinetic source (+) and sink (-) rate equation for the concentration of CBOD in the water column is expressed as:

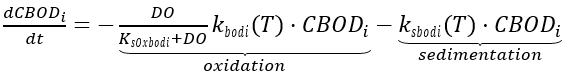                                  (60)

where

   CBOD_i = carbonaceous biochemical oxygen demand (mg-O₂ L^-1)

      k_bodi(T) = oxidation rate for CBOD i (d^-1)

     k_sbodi (T) = sedimentation rate for CBOD i (m d^-1)

       K_sOxbodi = half saturation oxygen constant for CBOD oxidation (mg-O₂ L^-1).

In Eq. 60, the subscript “i" denotes a specific type of CBOD. The model simulates ultimate CBOD, any CBOD input from boundary conditions or point sources must be in this same form. CBOD can also be determined by standard methods that measure the oxygen consumption of a filtered sample during laboratory incubation over a defined period. A commonly used water quality constituent is five-day CBOD (CBOD_5day) (mg-O₂ L^-1), which represents the amount of oxygen consumed when a sample is stored for five days in a dark environment at 20^oC. Consumption of organic carbon has been found to follow first-order exponential decay. CBOD_5day measurements are converted to CBOD based on individual CBOD decay rates as follows.

                                                                                                                  (61)

where

CBOD_5day = 5-day CBOD (mg-O₂ L^-1)

          k_bodi = oxidation rate for CBOD i at 20^oC (d^-1).

The conversion factor from CBOD_5day to CBOD varies depending on the source of the CBOD. Typical ratios for raw wastewater are 1.2 and 1.6 for primary or secondary wastewater (Thomann and Muller 1987). The concentrations of Total Organic Carbon (TOC) and Total Suspended Solids (TSS) in the water column are directly computed from the modeled carbon state variables. TOC represents the total amount of organic matter in natural water, encompassing both particulate (colloidal) and dissolved organic carbon forms, as well as CBOD and algal biomass. In NSMI, the concentration of TOC in the water column is calculated as follows.

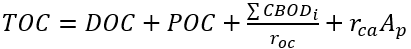                                                                          (62)

TSS encompass all inorganic suspended solids fractions as well as organic matter, including algae and particulate organic matter. The concentration of TSS in the water column is calculated as follows.

                                                                                                        (63)

The concentration of POM in the water column is calculated as:

                                                                                                                                (64)

where

       TOC = total organic carbon (mg-C L^-1)

         TSS = total suspended solids (mg L^-1).

Measurements of ultimate CBOD are rarely performed, making direct comparisons between CBOD_5day measurement and model outputs challenging. Therefore, it is essential to convert modeled CBOD into CBOD_5day or vice versa. The concentration of CBOD_5day in model outputs is calculated by aggregating contributions from dissolved organic matter, represented as both CBOD and DOC.

                                   (65)

where

           r_oc   = O₂:C ratio for carbon oxidation (mg-O₂ mg-C^-1)

       k_doc(T) = DOC oxidation rate (d^-1).

CBOD_5day reflects the oxidation of DOC and should be used for comparison with filtered laboratory CBOD_5day measurements. If CBOD_5day measurements are affected by algal respiration and the decay of algal carbon, a correction must be applied to the modeled CBOD to ensure a valid comparison with observed measurements.

Dissolved Oxygen

DO concentration is generally viewed as an indicator of the overall health of aquatic ecosystems. It is essential to account for all processes that exert an oxygen demand. Algae influence DO levels directly through photosynthesis and respiration, and indirectly through producing detrital organic carbon, which is subsequently dissolved and oxidized. Atmospheric reaeration can also contribute to DO levels when the concentration is below saturation. The sinks for DO include algal respiration, nitrification, oxidation of organic materials (particularly DOC, CBOD), sediment oxygen demand (SOD), and atmospheric reaeration when oxygen saturation is exceeded. When anaerobic conditions, the decay of organic materials significantly slows down, and organic decay rates are dependent on the amount of DO present in the water body.

In NSMI, the kinetic source (+) and sink (-) rate equation for the concentration of DO in the water column is as follows.

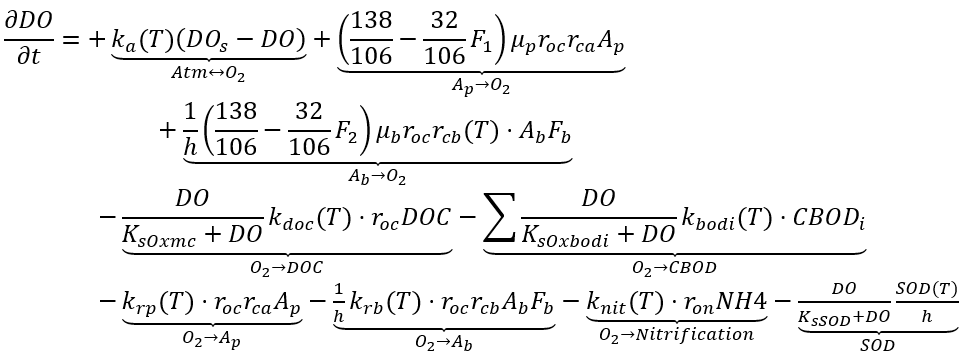                             (66)

where

         DO = dissolved oxygen (mg-O₂ L^-1)

        DO_s = dissolved oxygen saturation (mg-O₂ L^-1)

            k_a  = oxygen reaeration rate (d^-1)

           r_on = O₂:N ratio for nitrification (mg-O₂ mg-N^-1)

  SOD(T) = sediment oxygen demand (g-O₂ m^-2 d^-1)

         K_sSOD = half saturation oxygen constant for SOD (mg-O₂ L^-1).

When both CBOD and DOC are included in the model, it is crucial to to ensure that they are properly accounted for. CBOD, DOC, POC are commonly used to estimate the quantity of organic matter in natural waters. Typically, CBOD is specified as allochthonous inputs, while autochthonous organic matter is tracked of in the organic carbon compartments (DOC, POC). Care must be taken to avoid "double counting" organic matter, as this can affect DO levels when CBOD and organic carbon are included in the model simulation.

Various methods have been employed to estimate the DO saturation (DO_s) (Bowie et al. 1985). In NSMI, DO_s is calculated as a function of water temperature using the equation in APHA (1992).

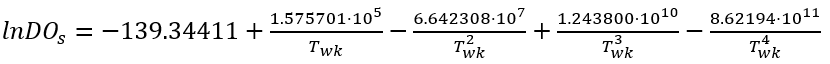                            (67)

In typical natural waters in temperate climates, the above equation shows that oxygen concentrations range from 14.621 mg/L at 0 ^oC to 6.413 mg/L at 40 ^oC.

DO saturation is also influenced by atmospheric pressure and salinity. The effect of atmospheric pressure on DO saturation is adjusted using a relationship developed by Benson and Krause (1984):

                                                                                                                       (68)

where

           p_atm = atmospheric pressure (atm)

          p_wv = vapor pressure (atm)

             α = correction coefficient.

The effect of salinity on DO saturation is adjusted according to the equation given in APHA (1992).

                                                              (69)

where

         Salt = salinity (ppt).

In Eq. 68, vapor pressure (p_wv) and the correction coefficient (α) depend on water temperature and are calculated using the equations provided in APHA (1992). If the concentration of DO exceeds the saturation level, it is referred to as oxygen supersaturation. The oxygen saturation level (DO%) is defined as follows:

                                                                                                                                                                    (70)

Oxygen reaeration refers to the transfer of oxygen across the air–water interface. This transfer is influenced by the difference in DO concentrations between the air and water, as well as the turbulence in the thin film of water adjacent to the surface. Such turbulence may be generated by wind shear or water currents. The oxygen reaeration rate (k_a) is typically estimated using hydraulic parameters and wind speed.

                                                                                                                                                   (71)

where

      k_aw(T) = wind derived oxygen reaeration velocity (m d^-1)

       k_ah(T) = flow derived oxygen reaeration rate (d^-1).

Numerous formulations have been developed to estimate oxygen reaeration rates. Most of these equations in the literature are derived from relatively small sets of laboratory or field data. NSMI includes eight flow derived oxygen reaeration equations (List of flow derived oxygen reaeration rate equations). The oxygen reaeration rate calculated from these equations is referenced to 20 ^oC and is subsequently adjusted to the local water temperature using an Arrhenius Equation.

List of flow derived oxygen reaeration rate equations

 u = water velocity (m s^-1), h = water depth (m), s_l = channel slope, B_t = top width of the channel (m), R_h = channel hydraulic radius (m), A_c = channel cross-sectional area (m²)

In addition, flow derived oxygen reaeration rates can be specified by the user and calculated in the model. NSMI includes thirteen equations or functions used for estimating wind derived oxygen reaeration (List of wind derived oxygen reaeration rate equations). These equations are commonly used to calculate oxygen reaeration for lakes and reservoirs. Wind speed is typically measured at an elevation of 10 m for the formulations listed in List of wind derived oxygen reaeration rate equations. To calculate the wind speed at this elevation in the middle of a water body, u_10m, an approach from Fang and Stefan (1994) can be applied to the wind speed measured at 10 m on land.

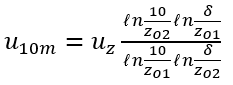                                                                                          (72)

where:

           W_z =  wind speed measured at 10 m height on land (m s^-1)   

           z_o1  =  roughness of land (assume 0.01 m)

           z_o2  =  roughness of water surface (assume 0.0001 m)

             d  =  thickness of wind boundary layer over smooth surface that is a function of the fetch length (m)

          u_w10 = wind speed measured 10 meters above the water surface (m s^-1).

List of wind derived oxygen reaeration rate equations

In Eq. 66, the SOD is a user specified zero-order rate at which DO is removed from the water column during the decomposition of organic material in bed sediment. Typical SOD estimates based on laboratory experiments range from 0.5 to 2.0 g-O₂ m^-2 d^-1 (USEPA 1985). A value of 0.5 g-O₂ m^-2 d^-1 is recommended for natural SOD, while 1.5 g-O₂ m^-2 d^-1 is suggested for the total oxygen demand (Manivanan 2008). However, these values may not apply to current studies.

In NSMI, user-specified sediment releases of nutrients include NH4, NO3 and DIP. These releases occur due to a gradient in nutrient concentration between the overlying water and the pore water of the benthic sediment. The impact of sediment nutrient release can be significant. The model assumes that positive fluxes indicate movement from sediment to water, while negative fluxes indicate movement from water to sediment. Sediment-water fluxes of NH4 and inorganic phosphorous most typically occur from sediment to water and are considered positive quantities. In contrast, the transfer of NO3 across the sediment-water interface is defined as a denitrification process, and NO3 can move in both directions, resulting in either positive or negative fluxes.

Dissolved Nitrogen Gas and Total Dissolved Gas

Dissolved nitrogen gas (N2) is primarily modeled to compute the total dissolved gas (TDG) in the water column. Nitrogen gas is the most abundant form of nitrogen in the atmosphere and can dissolve in water. The driving force behind this transfer process is the difference between the concentration of N2 in the water and its saturation level in the air. The kinetic rate equation for the concentration of N2 in the water column is expressed as:

                                                                               (73)

where

          N2  = dissolved nitrogen gas (mg L^-1)

         N2_s = nitrogen gas saturation (mg L^-1)

           k_aN2 = nitrogen gas reaeration coefficient (m d^-1).

The exchange process involves the coupled interaction of hydrodynamics and mass transfer between the atmosphere and the water column. Different constituents of air (e.g., N₂, O₂, CO₂) dissolve to varying degrees, with amounts that depend on temperature. At equilibrium, Henry’s Law describes the relationship between the amount of gas dissolved in water and the amount present in the atmosphere. The value of k_aN2 can be determined from the oxygen reaeration rate. The reaeration rate equations for N2 and DO are identical. The reaeration coefficient for N2 is scaled relative to oxygen reaeration rate by:

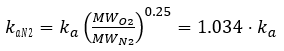                                                                        (74)

The oxygen reaeration rate (k_a) is either a user-defined parameter or estimated using hydraulic parameters and wind speed, as outlined in previous sections.

The N2 saturation in water (or solubility) is calculated using Henry's Law through the following processes. Air is a mixture of gases containing nitrogen, oxygen, carbon dioxide, and trace amounts of other gases. Assuming that only the major atmospheric gases are present, the total pressure of the dissolved gases is considered to be equal to the sum of the partial pressures of all gases dissolved in the water. According to Dalton's law of partial pressures, the total pressure exerted is calculated as the sum of the partial pressures of each individual gas (Colt 2012). 

                                                                                      (75)

where

           p_atm = atmospheric pressure (atm)

          p_wv = vapor pressure (atm)

         P_O2     = partial pressure of oxygen in the atmosphere (atm).

         P_N2    = partial pressure of N2 in the atmosphere (atm).

The actual vapor pressure can be derived from the known wet bulb temperature (T_wb), dew point temperature (T_d), or relative humidity (RH). Assuming that the mole fraction of N₂ in air is approximately 0.79, the partial pressure of N2 in air can then be calculated as:

                                                                                      (76)

Finally, the N2 saturation in water (or solubility) is determined using Henry's Law.

                                                                                                        (77)

where

         X_N2    = nitrogen gas saturation in molarity (mol L^-1)

       K_H(T)  =  Henry’s Law constant of N2 (mol L^-1 atm^-1)

         P_N2    = partial pressure of N2 in the atmosphere (atm).

                                          (78)

A variety of units have been used for K_H. In the above equation, the units of K_H are mol (L·atm)^-1 or M atm^-1. A typical value for the Henry’s law constant of N2 at 20°C is 7.1 ·10⁻⁴ M atm^-1.

While the units for gas solubility (X_N2) calculated from Henry's Law are mol L^-1, these are not commonly used in water quality modeling. In such modeling, the concentration of gases is typically represented in units like mg L^-1. The N2 saturation concentration in terms of mole is related to mass by the following relationship:

                                                                                                (79)

If the concentration of N2 exceeds its solubility, N2 becomes supersaturated. The N2 saturation level (N2%) is calculated using the following equation:

                                                                                                     (80)

Total Dissolved Gas (TDG) is often expressed in terms of the percent saturation or supersaturation. TDG saturation (TDG%) is determined by calculating the percent total dissolved gas pressure (TGP), based on the principle that the concentration of dissolved gas is proportional to its partial pressure.

                       (81)

In Eq. 81, only the partial pressures of DO and N2 are considered. The mole fraction of nitrogen in air is approximately 0.79, while the mole fraction of oxygen in air is approximately 0.21. Although the saturation of other minor gases, such as argon, carbon dioxide, may be important for understanding certain chemical and biological processes, they do not significantly contribute to TDG saturation.

The concentration of TDG in waters downstream of a reservoir or other hydraulic structures also depends on the geometric configuration of the spillway and the operating conditions. The effects of hydraulic structures, such as spillways and gates, on the reaeration of oxygen and nitrogen gases are not accounted for here. Otherwise, the concentrations of DO and N2 released from hydraulic structures need to be recalculated in the model.

Alkalinity and pH

Alkalinity measures the buffering capacity of a solution and is often referred to as water hardness. It is influenced by all the processes that yield or consume H⁺ or OH^- in the aquatic environment. In NSMI, the kinetic source (+) and sink (-) rate equation for the concentration of alkalinity in the water column is expressed as:

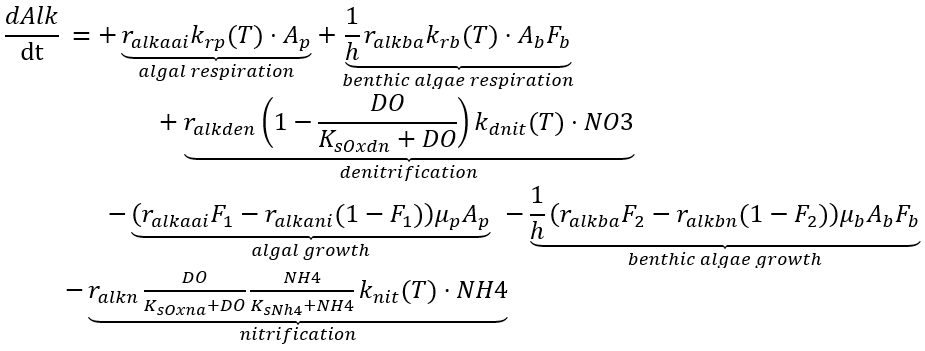          (82)

where

          Alk = alkalinity (eq L^-1)

          r_alkaa = ratio translating algal growth into Alk if NH4 is the N source (eq µg-Chl^-1)

          r_alkan = ratio translating algal growth into Alk if NO3 is the N source (eq µg-Chl^-1)

           r_alkn = ratio translating NH4 nitrification into Alk (eq mg-N^-1)

         r_alkden = ratio translating NO3 denitrification into Alk (eq mg-N^-1)

          r_alkba = ratio translating benthic algae growth into Alk if NH4 is the N source (eq mg-D^-1)

          r_alkbn = ratio translating benthic algae growth into Alk if NO3 is the N source (eq mg-D^-1).

The actual units for alkalinity in Eq. 73 are expressed in moles or equivalents per volume (moles/L or eq/L). However, laboratories typically measure and report alkalinity in units of C_aCO₃ equivalent (mg-C_aCO₃ L^-1), which corresponds to a solution containing specific amounts of calcium carbonate (C_aCO₃) dissolved in water. Naturally occurring alkalinity usually ranges between 400 and 500 mg L^-1. Consequently, alkalinity is expressed in units of “mg L^-1 C_aCO₃” in NSMI. Converting alkalinity from eq/L to “mg/L as CaCO3” accounts for the fact that one mole of carbonate (CO₃^2-) can neutralize two moles of acid (H⁺), meaning that .

The common constituents of alkalinity are HCO3^-, CO3^2-, and OH^-. HCO3^-, In surface water with a neutral pH typically constitutes more than 95% of the total alkalinity. Alkalinity is usually defined as:

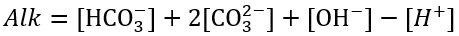                                                     (83)

and

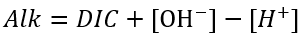                                                                                  (84)

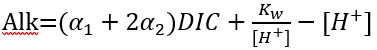                                                                           (85)

where

          H⁺ = hydronium ion (mol L^-1)

        OH^- = hydroxyl ion (mol L^-1).

pH is a measure of the H⁺ concentration and indicates the acidic or basic character of a solution at a given temperature. The pH scale from 0 to 14, with 7 representing neutrality. To compute pH in NSMI, users must enable DIC and alkalinity state variables. Once the unknown [H⁺] is determined from the nonlinear equation (Eq. 83), the pH is calculated as the negative logarithm of [H⁺].

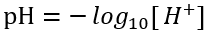                                                                                                          (86)

Eq. 83 is solved for [H⁺] using two numerical methods outlined by Chapra et al. (2008): (1) the Newton-Raphson method and (2) the Bisection method. The Newton-Raphson method utilizes the slope (tangent) of the function at the current iterative solution to determine the next iteration's solution. In contrast, the Bisection method is an incremental search approach that selects the next interval for iteration by dividing the current interval in half. Generally, the Newton-Raphson method converges more quickly than the Bisection method. However, it does not guarantee a solution in all cases.

Pathogen

A variety of indicators and enumerations exist for measuring pathogens, with their concentration in water often represented by CFU, which indicate viable bacterial numbers. Pathogens experience losses due to death, sunlight decay, and settling. The mortality of pathogens in the absence of sunlight is typically modeled as a first order kinetics. The depth-averaged effect of sunlight on the decay rate depends on surface solar radiation and the light attenuation coefficient. Additionally, pathogen settling losses are influenced by the number of organisms attached to particles. In NSMI, the kinetic source (+) and sink (-) rate equation for the concentration of pathogen in the water column is expressed as follows:

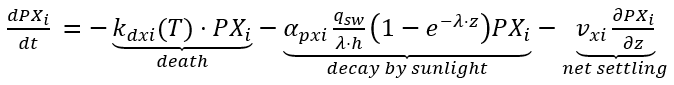            (87)

where

         PX_i = pathogen i ((cfu (100 mL) ^-1)

       k_dxi(T) = death rate for pathogen i (d^-1)

          q_sw = short-wave solar radiation flux (W m⁻²)

           a_pxi = light efficiency factor for pathogen decay

           v_xi = settling velocity for pathogen i (m d^-1).

In Eq. 78, the subscript “i" denotes a specific type of pathogen. The net settling loss rate, v_x, can be negative, zero, or positive, depending on the extent of resuspension, as benthic sediment may serve as a significant source of pathogens.