Download PDF
Download page Defining the Watershed Coordinate System.
Defining the Watershed Coordinate System
In "Setting the Geographic Coordinate System" explains how to specify the coordinate system of your watershed by accessing the Display Coordinate Information. This section provides more detailed information related to setting up the coordinate system for your watershed.
Accessing Display Coordination Information
The Display Coordinate Information editor is accessible from the Layer Selector which can be opened from any of the three ResSim modules. To open it:
- Select Layers from the View menu in the Main ResSim window. The Layer Selector will open
- Select Map Display Coordinates from the Maps menu of the Layer Selector.
- In the Display Coordinate Information editor, select Edit.
- The Map Coordinate Information editor will appear where you can set the appropriate coordinate information.
The above steps are illustrated in "Figure: Steps for Accessing the Coordinate System".
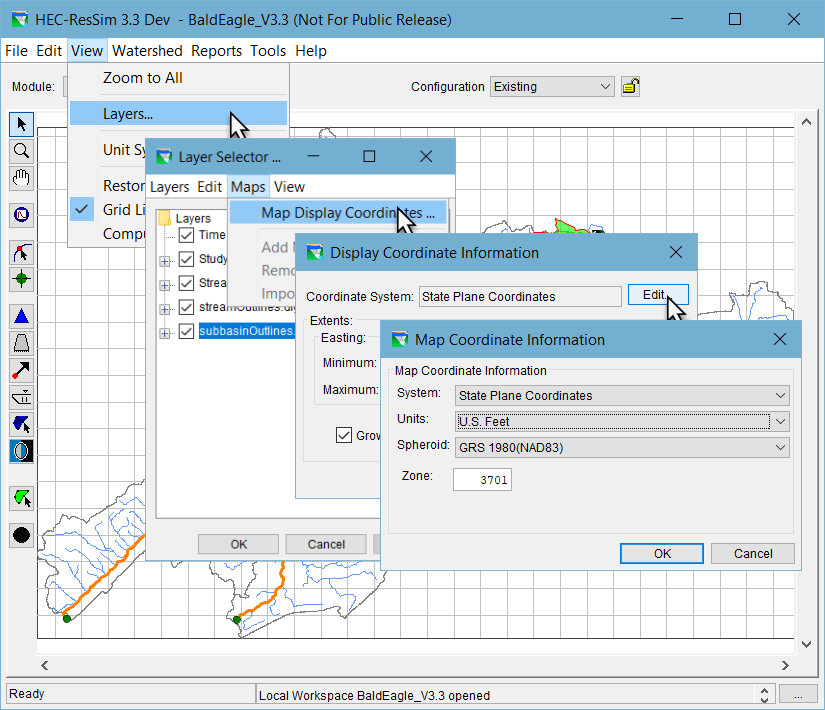
Figure: Steps for Accessing the Coordinate System
"Table: Available Map Coordinate Systems, Units, and Spheroid Options" shows the options available for System, Units, and Spheroid. When you choose specific coordinate systems, not all options are available from the Spheroid list. For example, choosing X-Y from the System list deactivates the Spheroid list. Additionally, when State Plane Coordinates is selected as the System, only Clarke 1886 and GRS 1980 are available choices from the Spheroid list.
Table: Available Map Coordinate Systems, Units, and Spheroid Options | ||
System | Units | Spheroid |
|---|---|---|
X-Y | U.S. Feet | X-Y does not allow selection of Spheroid |
Geographic | Radians |
|
Universal Transverse Mercator(2) | U.S. Feet |
|
State Plane Coordinates(3) | U.S. Feet |
|
Albers Equal-Area Conic(4) | U.S. Feet |
|
Lambert Conformal Conic(4) | U.S. Feet |
|
Transverse Mercator (5) | U.S. Feet |
|
Albers Equal-Area Conic (SHG) | U.S. Feet |
|
Polar Stereographic (HRAP) | U.S. Feet |
|
(2) Universal Transverse Mercator System also requires a UTM Zone to be entered | ||
(3) State Plane Coordinates also requires a numeric Zone to be entered (e.g., 3701) | ||
(4) Albers Equal-Area Conic and Lambert Conformal Conic also require the following: *Latitude for the first and second standard parallel, *Longitude of the central meridian, *Latitude of the projection origin, *False easting and northing | ||
(5) Transverse Mercator also requires the following entries: | ||
Coordinate System Options
The following sections describe each of the Coordinate Systems that are available from the Map Coordinate Information editor. With one exception, all require you to select distance Units and a Spheroid definition. Each spheroid definition inherently describes a prime meridian and a datum.
The options for distance Units include:
- (U.S. Feet
- Meters
- International Feet
The options for Spheroid definition include:
- Clark 1866(NAD27)
- WGS 72
- GRS 1980(NAD83)
- WGS 84
Sphere of Radius 6371200 Meters
X-Y System
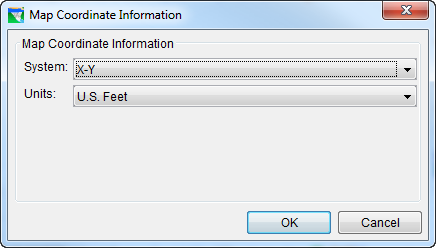
Figure: X-Y Coordinate System
X-Y is a simple Cartesian coordinate system ("Figure: X-Y Coordinate System").
Geographic System
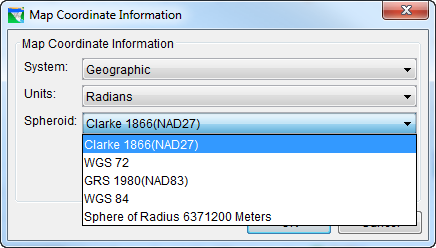
Figure: Geographic Coordinate System - Spheroid List
A Geographic coordinate system ("Figure: Geographic Coordinate System - Spheroid List") defines locations on the earth using a three-dimensional spherical surface. This coordinate system differs from the others in that the Units are not of distance but rather angle. The Units options include:
- Radians
- Seconds of Arc
- Degrees of Arc
Transverse Mercator System and Universal Transverse Mercator (UTM) System
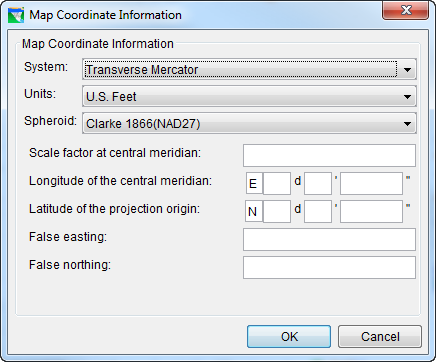
Figure: Map Coordinate Information Transverse Mercator System
The Transverse Mercator coordinate system represents the earth as a spheroid that has been flattened onto a transverse (sideways) cylinder such that each longitude line is equally spaced and parallel to one another. Small shapes are well represented because this projection preserves angular relationships, but area becomes increasingly distorted the further you get from the equator (toward the Polar Regions).
The Universal Transverse Mercator (UTM) coordinate system is a special implementation of the Transverse Mercator system that divides the globe into a specific set of 60 6° north-south segments or zones. The limits of each zone extent to 84 N and 80 S. Each zone is divided into a north and south half at the equator. The Polar Regions use the Universal Polar Stereographic coordinate system.
For the Transverse Mercator coordinate system ("Figure: Map Coordinate Information Transverse Mercator System"), you must choose both the Units (U.S. Feet, Meters, or International Feet) and Spheroid.
Additional required information includes: Scale factor at central meridian; Longitude of the central meridian; Latitude of the projection origin; False easting; and False northing.
When specifying latitudes, use N or S. For longitudes, use E or W. You may either type these into the fields or use the SPACEBAR on your keyboard to toggle between the acceptable entries (after placing your cursor in the first box of either the latitude or longitude field).
The Universal Transverse Mercator system ("Figure: UTM Coordinate System") is a specialized form of the Transverse Mercator projection. It uses a simple Cartesian coordinate system to represent locations on the earth. It represents the earth as a spheroid divided into 60 6° north-south segments or zones, flattens (transforms) each segment onto a transverse (sideways) cylinder, and applies an X-Y coordinate system to it. To use this system for your watershed, you must select:
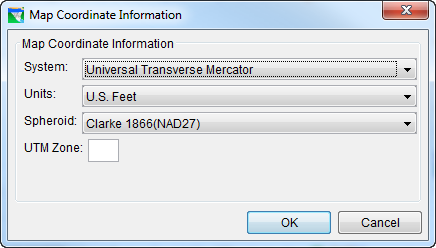
Figure: UTM Coordinate System
- Distance Units (U.S.)
- Spheroid definition
UTM Zone
State Plane Coordinates System

Figure: State Plane Coordinate System
The State Plane coordinate system ("Figure: State Plane Coordinate System") is a set of 124 geographic zones covering the 50 US states and US territories. It uses a simple Cartesian coordinate system to specify locations rather than a more complex spherical coordinate system. This system requires that you select:
- Distance Units
- Spheroid definition:
- Clarke 1866 (NAD27)
- GRS 1980(NAD83)
- Zone
Albers Equal-Area Conic System and Lambert Conformal Conic System
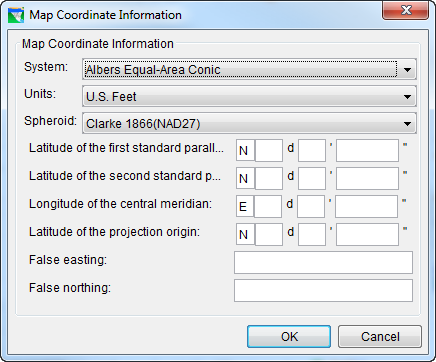
Figure: Albers Equal-Area Conic Coordinate System
The Albers Equal-Area Conic coordinate system ("Figure: Albers Equal-Area Conic Coordinate System") is based on a projection of a horizontal section of the earth onto a cone placed directly above the pole. The section of the earth that is projected is defined by two standard parallels—circles around the earth parallel to the equator. The Albers projection preserves the area of each section at the expense of a small distortion of distance (shape).
Like Albers, the Lambert Conformal Conic coordinate system is based on a projection of a horizontal section of the earth onto a cone placed directly above the pole. The Lambert Conformal Conic differs from the Albers Equal Area Conic projection because it preserves distances (shape) within each section at the expense of a small error in area.

Figure: Map Coordinate Information Lambert Conformal Conic System
These projections are best for regions that are predominately east-west in orientation and are best applied in the middle latitudes (the zones nearer the equator). The difference between the first and second parallels should not exceed 30-35 degrees.
To use one of these coordinate systems for your watershed, you must specify quite a few parameters:
- Distance Units
- Spheroid definition
- Latitude of the two standard parallels
- Longitude of the central meridian
- Latitude of the projection origin
- False easting—a value for the origin of the x-coordinates
- False northing—a value for the origin of the Y-coordinates
When specifying latitudes, use N or S. For longitudes, use E or W. You may either type N, S, E, or W into the fields, or use the SPACEBAR on your keyboard to toggle through the acceptable entries (after placing your cursor in the first box of either the latitude or longitude field).
Albers Equal-Area Conic (SHG) System

Figure: Map Coordinate Information Albers Equal-Area Conic (SHG) System
The SHG version of the Albers Equal-Area Conic (SHG) coordinate system ("Figure: Map Coordinate Information Albers Equal-Area Conic (SHG) System") displays a set of default parameters. These parameters cannot be changed. If you must change them, use instead the Albers Equal Area Conic system described above.
Polar Stereographic (HRAP) System
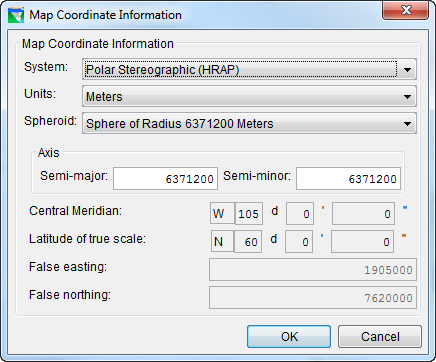
Figure: Map Coordinate Information Polar Stereographic (HRAP) System
The Polar Stereographic (HRAP) coordinate system ("Figure: Map Coordinate Information Polar Stereographic (HRAP) System")is used by the National Weather Service for describing their NEXRAD precipitation grids. The editor for this coordinate system shows the default parameters that define the HRAP system. These parameters cannot be changed.