Download PDF
Download page Applying the Initial and Constant Loss Method.
Applying the Initial and Constant Loss Method
Return to Introduction to the Loss Rate Tutorials.
Last Modified: 2025-01-29 16:31:06.348
HEC-HMS version 4.13-beta.4 was used to created this tutorial. You will need to use HEC-HMS version 4.13-beta.4, or newer, to open the project files.
Download the initial project files here:
Note: The initial project file is the same for the Initial and Constant Loss Method, the Green and Ampt Loss Method, and the Deficit and Constant Loss Method tutorials. If you are completing all three tutorials, the files only need to be downloaded once.
Overview
In this tutorial you will apply the HEC-HMS Initial and Constant loss method to a modeling application. Initial parameter estimates will be estimated using GIS information and the model will be calibrated through trial and error.
Background
The Initial and Constant loss method uses a hypothetical single soil layer to account for changes in moisture content. While this method is very simple, it is widely used to model watersheds that lack detailed subsurface information. Since no means for extracting infiltrated water is included, this method should only be used for event simulation. The underlying concept of the Initial and Constant loss method is that the maximum potential rate of precipitation loss, fc, is constant and unchanging during a simulation. Thus, if the precipitation rate, pt, is less than fc, no runoff will occur. An initial loss, Ia, can be specified to represent the volume of precipitation that is expected to be lost prior to the onset of runoff initiation. Until the accumulated precipitation volume, pi, exceeds Ia, no runoff will occur. After Ia has been satisfied, runoff will only occur if and when pt is in excess of fc. Parameters that are required to utilize this method within HEC-HMS include the Initial Loss [inches or millimeters] and Constant Rate [in/hr or mm/hr]. The Directly Connected Impervious Area [percent] is an optional parameter and can be specified by the user.
Estimate Initial Parameter Values
A Note on Parameter Estimation
The values presented in this tutorial are meant as initial estimates. This is the same for all sources of similar data including Engineer Manual 1110-2-1417 Flood-Runoff Analysis and the HEC-HMS Technical Reference Manual. Regardless of the source, these initial estimates must be calibrated and validated.
Initial Loss
The Initial Loss defines the volume of water that is required to fill the soil layer at the start of the simulation. This parameter is typically defined using the product of the soil moisture state at the start of the simulation and an assumed active layer depth, but it should be calibrated using observed data. In order to estimate an appropriate Initial Loss, the antecedent conditions at the beginning of September 2018 must be investigated. Daily average humidity, daily precipitation accumulation, daily average temperature, and daily average wind speed for August 2018 are shown below.
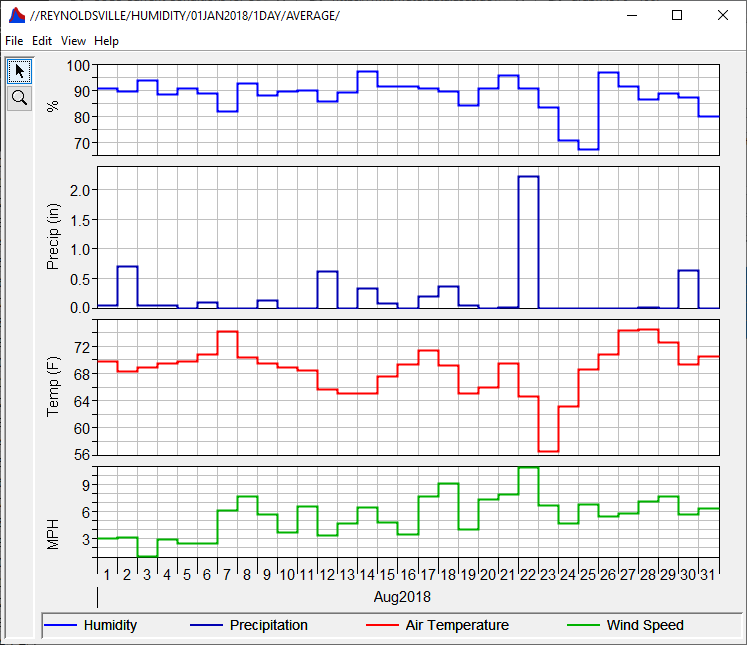
Use the figure above and the following information to answer Question 1. Assume that the soil within the study area:
- Was completely saturated by rainfall on August 22, 2018 and
- Requires approximately 14 days with no rain to completely dry under normal, summer conditions
Question 1: Estimate an Initial Loss (in inches) for the study area at the beginning of September 2018.
A reasonable Initial Loss is approximately 2 inches. However, this parameter must be calibrated using observed data.
Constant Rate
The Constant Rate defines the rate at which precipitation will be infiltrated into the soil layer after the initial loss volume has been satisfied. Typically, this parameter is equated with the saturated hydraulic conductivity of the soil which is defined as the rate at which water moves through a unit area of saturated soil in a unit time under a unit hydraulic gradient. To estimate saturated hydraulic conductivity throughout the study area, Gridded Soil Survey Geographic (gSSURGO) data for Pennsylvania was obtained from the U.S. Department of Agriculture's Geospatial Data Gateway. Using GIS tools, surficial soil textures were then extracted from the gSSURGO data and are shown below. Also, the percent of the study area encompassed by each soil texture is shown in Table 1.
A tutorial describing how gSSURGO data can be obtained and formatted for use within HEC-HMS can be found here.
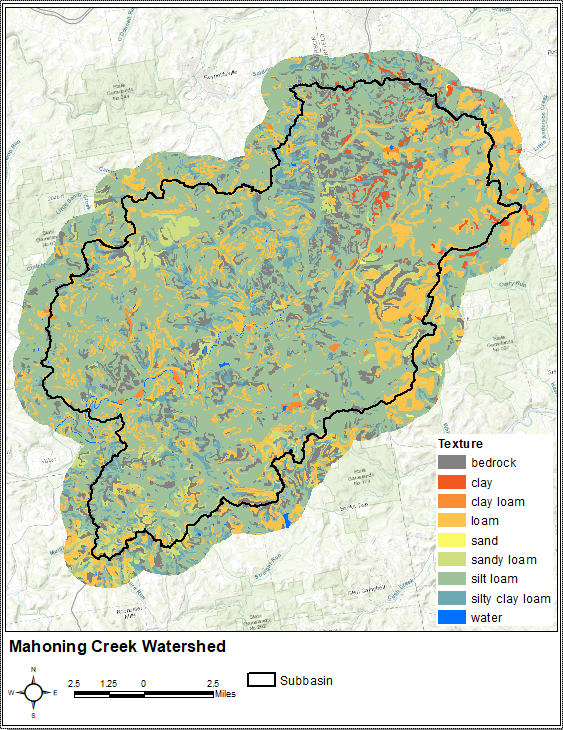
Table 1. Soil Textures Within the Study Area
Texture | % of Study Area |
|---|---|
| Sand | 0.1 |
| Loamy Sand | 0.0 |
| Sandy Loam | 3.7 |
| Loam | 17.1 |
| Silt Loam | 59.8 |
| Sandy Clay Loam | 0.0 |
| Clay Loam | 0.5 |
| Silty Clay Loam | 6.9 |
| Sandy Clay | 0.0 |
| Silty Clay | 0.0 |
| Clay | 0.9 |
| Bedrock | 10.7 |
These surficial soil textures can be used to estimate initial parameter values for nearly all loss methods within HEC-HMS, including the Initial and Constant loss method. For instance, Rawls, Brakensiek, and Miller (1983) assembled data from thousands of soil samples located throughout the United States and related soil textures to various parameters that are useful within hydrologic modeling. The saturated hydraulic conductivity of various soil textures is shown in Table 2.
Table 2. Soil Textures and Saturated Hydraulic Conductivity, reproduced from Rawls, Brakensiek, and Miller (1983)
Texture | Saturated Hydraulic Conductivity |
|---|---|
Sand | 4.6 |
Loamy Sand | 1.2 |
Sandy Loam | 0.4 |
Loam | 0.1 |
Silt Loam | 0.3 |
Sandy Clay Loam | 0.06 |
Clay Loam | 0.04 |
Silty Clay Loam | 0.04 |
Sandy Clay | 0.02 |
Silty Clay | 0.02 |
Clay | 0.01 |
Use the Mahoning Creek surficial soil textures map, Table 1, and Table 2 to answer the following questions.
Question 2: What are the top five predominant soil textures throughout the study area?
Silt loam, loam, bedrock, silty clay loam, and sandy loam are the five most predominant soil textures (by area) throughout the study area. In fact, these five soil textures cover over 98% of the total study area. The remaining soil textures account for a very small percentage of the total area and can be disregarded.
Next, use Table 2 to answer the following question. Also, (conservatively) assume that bedrock has a saturated hydraulic conductivity of 0 in/hr.
Question 3: What is the saturated hydraulic conductivity for the top five predominant soil textures found when answering Question 2?
Silt loam = 0.3 in/hr, loam = 0.1 in/hr, bedrock = 0 in/hr, silty clay loam = 0.04 in/hr, and sandy loam = 0.4 in/hr.
Finally, estimate an average (i.e. representative) saturated hydraulic conductivity for the study area using your answers to the previous two questions. Don't spend too much time being overly precise; instead, quickly estimate the fraction of the study area that is encompassed by each predominant soil texture and multiply by the corresponding saturated hydraulic conductivity. Once you've done that for each of the five predominant soil textures, sum the values.
Question 4: What is an average (i.e. representative) saturated hydraulic conductivity for the study area?
Silt loam covers approximately 60% of the total area, loam covers approximately 17% of the total area, bedrock covers approximately 10% of the total area, silty clay loam covers approximately 7% of the total area, and sandy loam covers approximately 3% of the total area. Thus, (0.6 * 0.3 in/hr) + (0.17 * 0.1 in/hr) + (0.1 * 0.0 in/hr) + (0.07 * 0.04 in/hr) + (0.03 * 0.4 in/hr) = 0.2 in/hr.
Directly Connected Impervious Area
Directly connected impervious areas are surfaces where runoff is conveyed directly to a waterway or stormwater collection system. These surfaces differ from disconnected impervious areas where runoff encounters permeable areas which may infiltrate some (or all) of the runoff prior to reaching a waterway or stormwater collection system. Within HEC-HMS, no loss calculations are carried out on the percentage of the subbasin that is specified as impervious area; all precipitation that falls on that portion of the subbasin becomes excess precipitation and subject to direct runoff. Within this tutorial, a directly connected impervious area percentage of 0 will be assumed.
Modify the Existing HEC-HMS Project
Now that you've estimated initial parameters, begin modifying the existing HEC-HMS project.
- Open the Punxsutawney_Loss_Methods project and then open the Mahoning_InitialConstant basin model.
- Select the Mahoning Creek subbasin element.
- On the Subbasin tab, change the Loss Method from None to Initial and Constant.
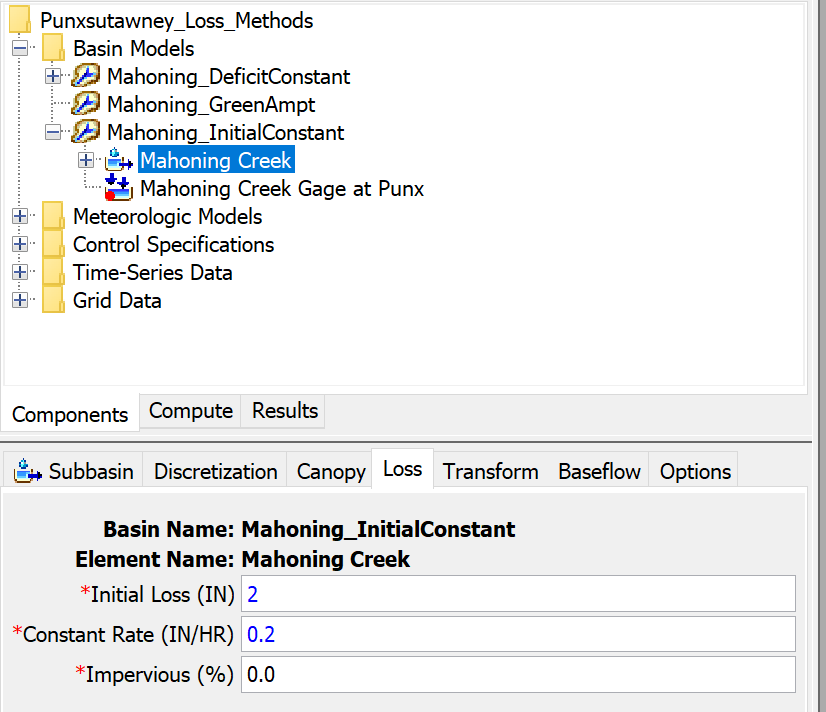
- Select the Loss tab to open the Initial and Constant Component Editor.
- Enter the initial loss, constant rate, and directly connected impervious area values that were estimated in the previous section. The Initial and Constant Component Editor should resemble Figure 3.
- Create a new simulation run by clicking Compute | Create Compute | Simulation Run.
- Name the new simulation run "Sept2018_InitialConst". Select Next>.
- Select the Mahoning_InitialConstant basin model. Select Next>.
- Select the MRMS meteorologic model. Select Next>.
- Select the September 2018 control specifications. Click the Finish button.
- Select the Sept2018_InitialConst simulation run from the Compute toolbar.

- Press the Compute All Elements button,
 , to run the simulation.
, to run the simulation. - Select the Mahoning Creek subbasin element and click the the Result Graph button,
 , and the Summary Table button,
, and the Summary Table button,  .
. - Leave the summary table and plot open so you can see results change as you modify the loss method parameters. The observed streamflow is represented by the black dotted line and the model's computed streamflow is represented by the solid blue line.
- Notice that there is much less computed runoff than observed flow. This is confirmed within the Summary Table which shows large differences in observed and computed runoff volumes and peak flows, and poor statistical metrics.
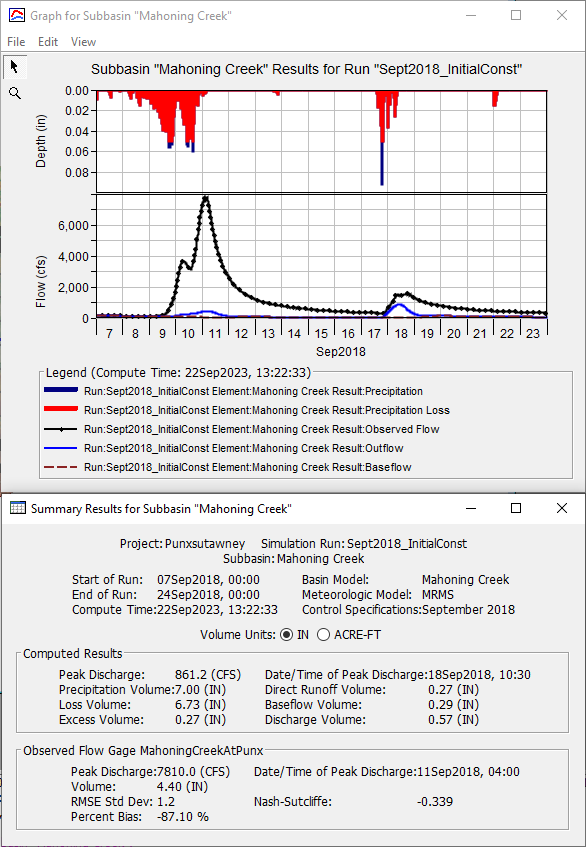
- To better match the observed runoff, the Initial and Constant loss method parameters must be calibrated.
Calibrate the Model
Calibrating a model to afford better agreement between computed and observed runoff oftentimes requires simultaneous changes to more than just one process (e.g. calibrate both loss and baseflow at the same time). However, within this tutorial, only the Initial and Constant loss method parameters will be modified.
- Begin by modifying the loss parameters to approximately match the initiation of runoff.
- Change the Initial Loss to 1 inch and the Constant Rate to 0.1 in/hr and rerun the simulation.
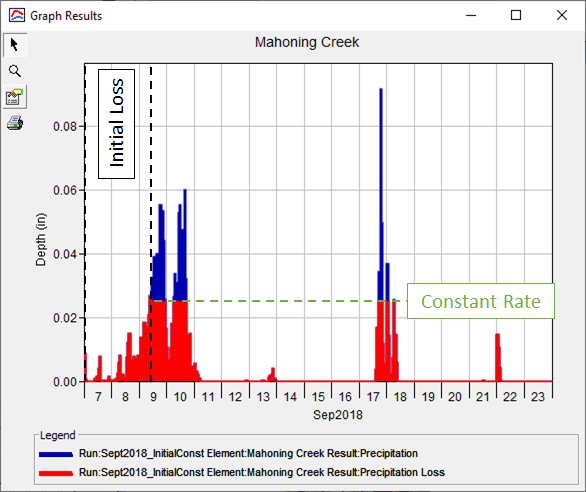
- The precipitation (dark blue) and precipitation loss (red) hyetographs for the Mahoning Creek subbasin element are plotted below Notice that the precipitation volume from the start of the simulation through approximately 09Sep2018 12:00 is used to satisfy the initial loss (a volume of 1 inch). Afterwards, precipitation is infiltrated at a rate of 0.1 in/hr. When using a time step of 15 minutes, the effective rate is 0.025 inches / 15 minutes (i.e. 0.1 in/hr * 15 / 60).
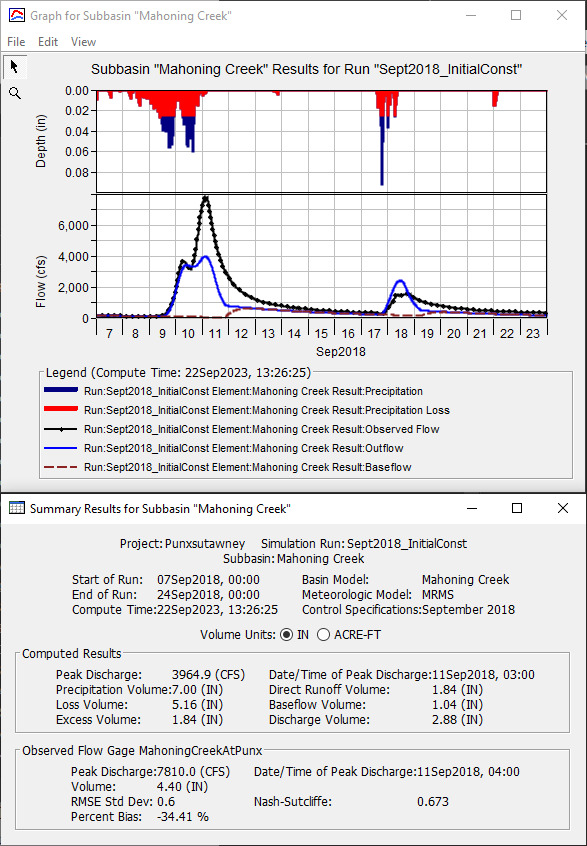
- When looking at the Result Graph and Summary Table for the Mahoning Creek subbasin element, the computed hydrograph begins to rise at approximately the same time as the observed hydrograph, as shown below. However, the computed runoff volume (2.88 inches) is still much less than the observed runoff volume (4.4 inches) so further modifications are required.
- Continue modifying the loss parameters to approximately match the observed runoff volume.
- Change the Constant Rate to 0.05 in/hr and rerun the simulation.
- Notice that the computed runoff volume is now slightly greater than the observed runoff volume (5.01 vs 4.4 inches), as shown below. Also, the computed peak flow rate, 7044 cfs, more closely matches the observed peak flow rate. However, the shape of the computed runoff hydrograph doesn't match the observed hydrograph shape on September 9th and 10th; in particular, the computed runoff is much greater than the observed runoff within those two days.
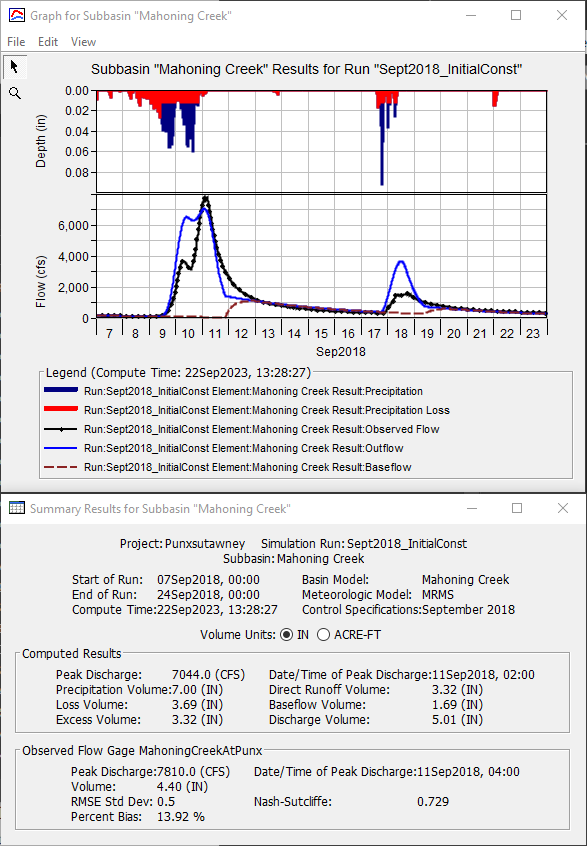
- To reduce the amount of runoff on September 9th and 10th, increase the Initial Loss to 1.75 inches and rerun the simulation.
- Notice that the computed runoff volume is now approximately equal to the observed runoff volume (4.49 vs 4.4 inches), as shown below. Also, there is better agreement between the shapes of the computed and observed hydrographs on September 9th and 10th.
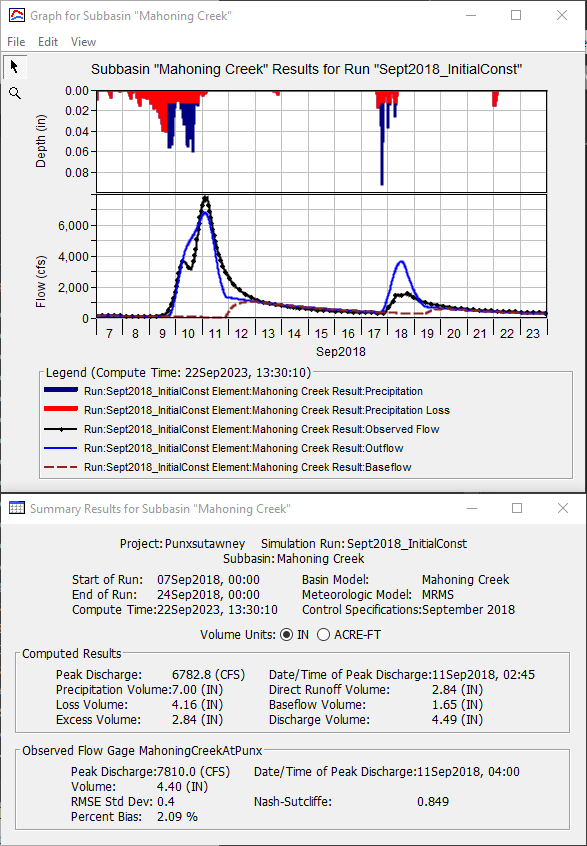
- Continue adjusting the Initial and Constant loss method parameters in an attempt to simultaneously best match the peak flow rate, runoff volume, and hydrograph shape. Record your RMSE Std Dev, Percent Bias, and Nash-Sutcliffe statistical metrics as you adjust model parameters.
- At this point, it should be apparent that simultaneously matching peak flow rate, runoff volume, and hydrograph shape can be difficult.
- For instance, the "double peak" runoff response within the observed results between September 9th - 11th is nearly impossible to recreate when using a single subbasin. This type of "signature" suggests two discrete pulses of runoff. To better match this response, two or more subbasins should be delineated.
Summary Questions
Question 5. What were the final Initial and Constant loss method parameters and corresponding RMSE Std Dev, Percent Bias, and Nash-Sutcliffe statistical metrics for the calibrated model?
Using an initial loss of 1.8 inches and a constant loss rate of 0.04 in/hr offers an RMSE Std Dev, Percent Bias, and Nash-Sutcliffe statistical metrics of 0.4, 12.32%, and 0.818, respectively, as shown below. However, these are by no means the only parameter combinations that can result in acceptable model calibration.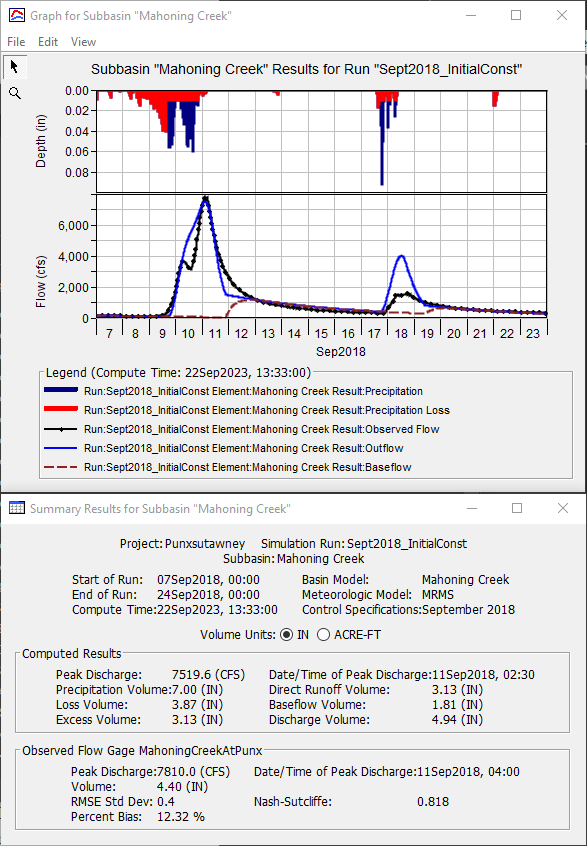
Question 6. Is it possible to reduce the computed runoff response on September 17th - 18th while not adversely affecting the computed runoff response on September 9th - 12th when using the Initial and Constant loss method? If not, why?
No. When using the Initial and Constant loss method, after the Initial Loss has been satisfied, the Constant Rate is the only means by which precipitation can be lost. In this instance, the Initial Loss is satisfied on September 9th. Increasing the Constant Rate to reduce the computed runoff on September 17th - 18th will unfavorably affect the runoff response on September 9th - 12th.
The Initial and Constant loss method does not include a way for infiltrated water to be extracted through evapotranspiration. In fact, a warning message is written to the messages panel:
WARNING 45231: Transpiration is not computed for Initial and Constant loss method in subbasin "Mahoning Creek".
If this is important to the specific application at hand, another loss method that can simulate these processes (e.g., Layered Green and Ampt, Deficit and Constant, Soil Moisture Accounting, etc.) should be used.
Download the final project files here:
Note: The final project file is the same for the Initial and Constant Loss Method, the Green and Ampt Loss Method, and the Deficit and Constant Loss Method tutorials. If you are completing all three tutorials, the files only need to be downloaded once.
Continue to Applying the Green and Ampt Loss Method.
