Return to Introduction to the Channel Routing Tutorials

Overview

In this tutorial you will apply the HEC-HMS Lag routing method to a modeling application.  Initial parameter estimates will be estimated using GIS and observed information and the model will be calibrated through trial and error.

HEC-HMS version 4.12-beta.2 was used to create this tutorial.  You will need to use HEC-HMS version 4.12-beta.2, or newer, to open the project files.

Download the initial project files here:

Reach_Routing_v4.12_start.zip

Background

The lag routing method is the most simplistic hydrologic routing method available for use within HEC-HMS.  This method can only represent the translation of flood waves and does not include any representation of attenuation or diffusion processes.  Inflow to the reach is delayed in time by a user-specified amount of time.  Consequently, it is best suited to short stream segments with a predicable travel time that doesn't vary with changing conditions.  Parameters that are required to utilize this method within HEC-HMS include the initial conditions and lag time [minutes].

Estimate Initial Parameter Values

Lag Time

Lag time is the amount of time (i.e. travel time) that the inflow hydrograph will be translated as it moves through the reach.  This parameter can be estimated in multiple ways including:

  • Using known hydrograph data.
  • Comparing flow length to a flood wave velocity.
  • Using regression equations which were developed from observed data in a similar region.

Using Known Hydrograph Data

The travel time of a flood wave moving through a reach can be estimated by taking the difference between "similar points" on known inflow and outflow hydrographs.  The similar points can be the peaks of either hydrograph, the centroid of the area underneath each hydrograph, or between some reference flow on the rising limb of either hydrograph.  The inflow and outflow hydrographs for this tutorial are shown and detailed within Figure 1.

Figure 1. Hydrographs

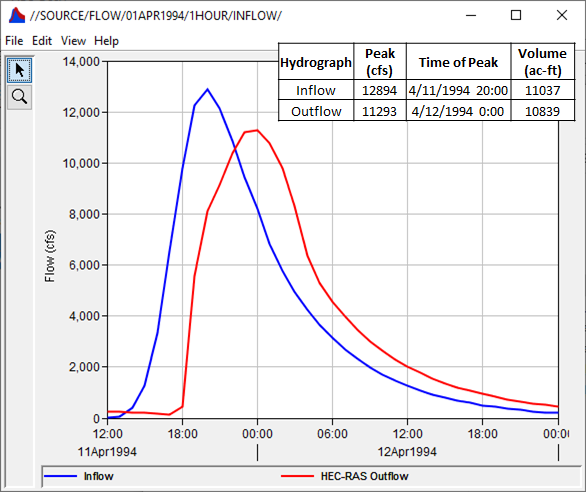
Use Figure 1 to answer the following questions.

Question 1: Use the time of peak for both hydrographs shown in Figure 1 to estimate a representative travel time (in hours) for this event.

The inflow and outflow time of peak are 4/11/1994 20:00 and 4/12/1994 00:00, respectively.  The difference in time between these two points is 4 hours.

Question 2: Use the approximate centroid of the area beneath each hydrograph to estimate a representative travel time (in hours) for this event.

The centroid of the area beneath the inflow hydrograph lies at approximately 4/11/1994 21:00.  The centroid of the area beneath the outflow hydrograph lies at approximately 4/12/1994 00:00.  The difference in time between these two points is 3 hours.

Question 3: For a reference flow of 6500 cfs on the rising limb, estimate a representative travel time (in hours) for this event.

The inflow hydrograph reaches 6500 cfs at approximately 4/11/1994 17:00.  The outflow hydrograph reaches 6500 cfs at approximately 4/11/1994 19:30.  The difference in time between these two points is 2.5 hours.


Comparing Flow Length to a Flood Wave Velocity

The travel time, T, of a flood wave moving through a reach can also be estimated by dividing the length of the reach, L, by the flood wave velocity, Vw:

T=\frac{L}{V_{w}}

To estimate a flood wave velocity, multiple approaches can be used including:

  • Manning's Equation (Manning, 1891)
  • Kleitz-Seddon Law (Seddon, 1900)

This tutorial will make use of the Kleitz-Seddon Law which can be written as:

V_{w}=\frac{1}{B} \frac{d Q}{d y}

where B = the top width of the water surface and \frac{d Q}{d y} = slope of the flow-stage rating curve; both of these variables must be estimated for the flow rate in question and at a cross section that is representative of the routing reach.  The USGS maintains a flow-stage rating curve for the stream gage at Punxsutawney and is shown in Figure 2.

Figure 2. Flow-Stage Rating Curve at Punxsutawney

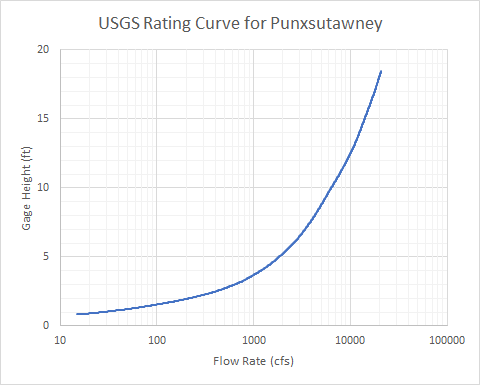
Use the previously-shown equations and Figure 2 to answer the following questions.  Assume the following:

  • The length of the reach within this example is 68860 feet.
  • The slope of the rating curve shown in Figure 2 at a reference flow of 6500 cfs is approximately 1316 cfs / ft.
  • The top width of Mahoning Creek at a reference flow of 6500 cfs is approximately 200 ft.

Question 4: For a reference flow of 6500 cfs, estimate a representative flood wave velocity (in ft / s) using the Kleitz-Seddon Law.

V_{w}=\frac{1}{B} \frac{d Q}{d y}

V_{w}=\frac{1}{200 ft} * 1316 \frac{cfs} {ft}

V_{w}=6.58 \frac{ft}{s}


Question 5: Using the previously-computed representative flood wave velocity, estimate a representative travel time (in hours) for this event.

T=\frac{L}{V_{w}}

T=\frac{68860 ft}{6.58 \frac{ft}{s}} * \frac{1 min}{60 sec} * \frac{1 hour}{60 min}

T=2.9 hrs


Question 6: Do you think a single, representative travel time can be estimated for both large and small flood events?  Do you have any reservations about the use of a single value to represent the travel time through a reach?

Estimating a single, representative travel time for flood events large and small is difficult (if not impossible) in real world streams.  In general, the speed at which a flood wave moves depends upon the depth of flow.  For instance, within most stream systems, larger floods (with greater depths) propagate faster than smaller floods (which have shallower depths).  Also, the speed at which a flood wave moves through a reach depends upon the geometry of the stream in question.  Top width, flow area, effective roughness, and even the flow length (due to increasing/decreasing sinuosity) of a stream can change with the magnitude of an event.  As such, the travel time through a reach depends upon the event and reach in question.  Channel routing parameters, like travel time, must be calibrated and validated based upon the model's intended use.


Modify the Existing HEC-HMS Project

Now that you've estimated initial parameters, begin modifying the existing HEC-HMS project.

  1. Open the Punxsutawney project and then open the Mahoning Creek Basin Model.
  2. Select the Mahoning Creek reach element.
  3. Change the routing method to Lag.
  4. Select the Routing tab to open the Lag Component Editor.
  5. Make sure the Initial Type is set to Discharge = Inflow.
  6. Enter one of the previously-determined lag times (in minutes, NOT hours) that were estimated in the previous section.  The Lag Component Editor should resemble Figure 3.
    Figure 3. Lag Routing Component Editor
  7. Create a new simulation run by clicking Compute | Create Compute | Simulation Run.
    1. Name the new simulation run "April1994_Lag".
    2. Select the Mahoning Creek basin model.
    3. Select the NoRain meteorologic model.
    4. Select the April 1994 control specifications.
  8. Select the April1994_Lag simulation run from the Compute toolbar, .
  9. Press the Compute All Elements button,  , to run the simulation.
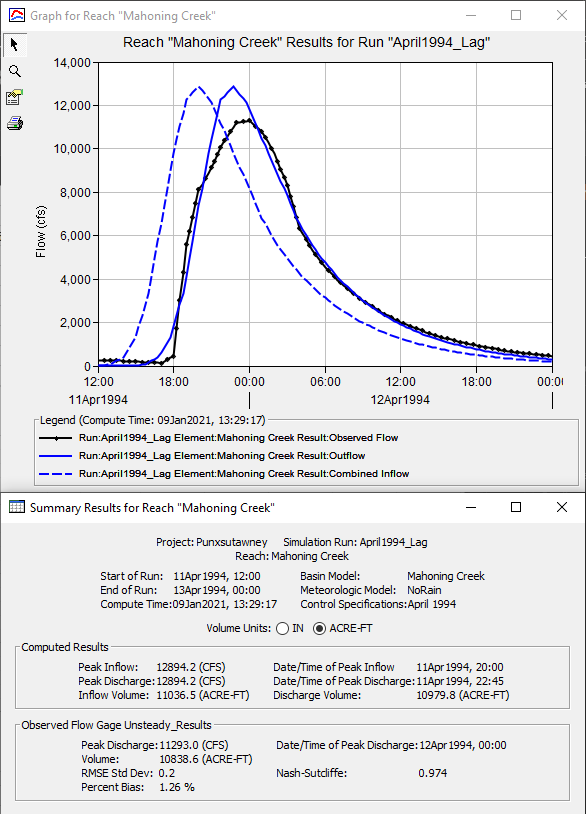
  10. View the result graph, , and summary table, , for the Mahoning Creek reach element, as shown in Figure 4.
    1. Leave the summary table and plot open so you can see results change as you modify the routing method parameters.
    2. Notice the computed peak discharge, time to peak discharge, and discharge hydrograph shape differ from the observed data.  This is confirmed within the summary table.
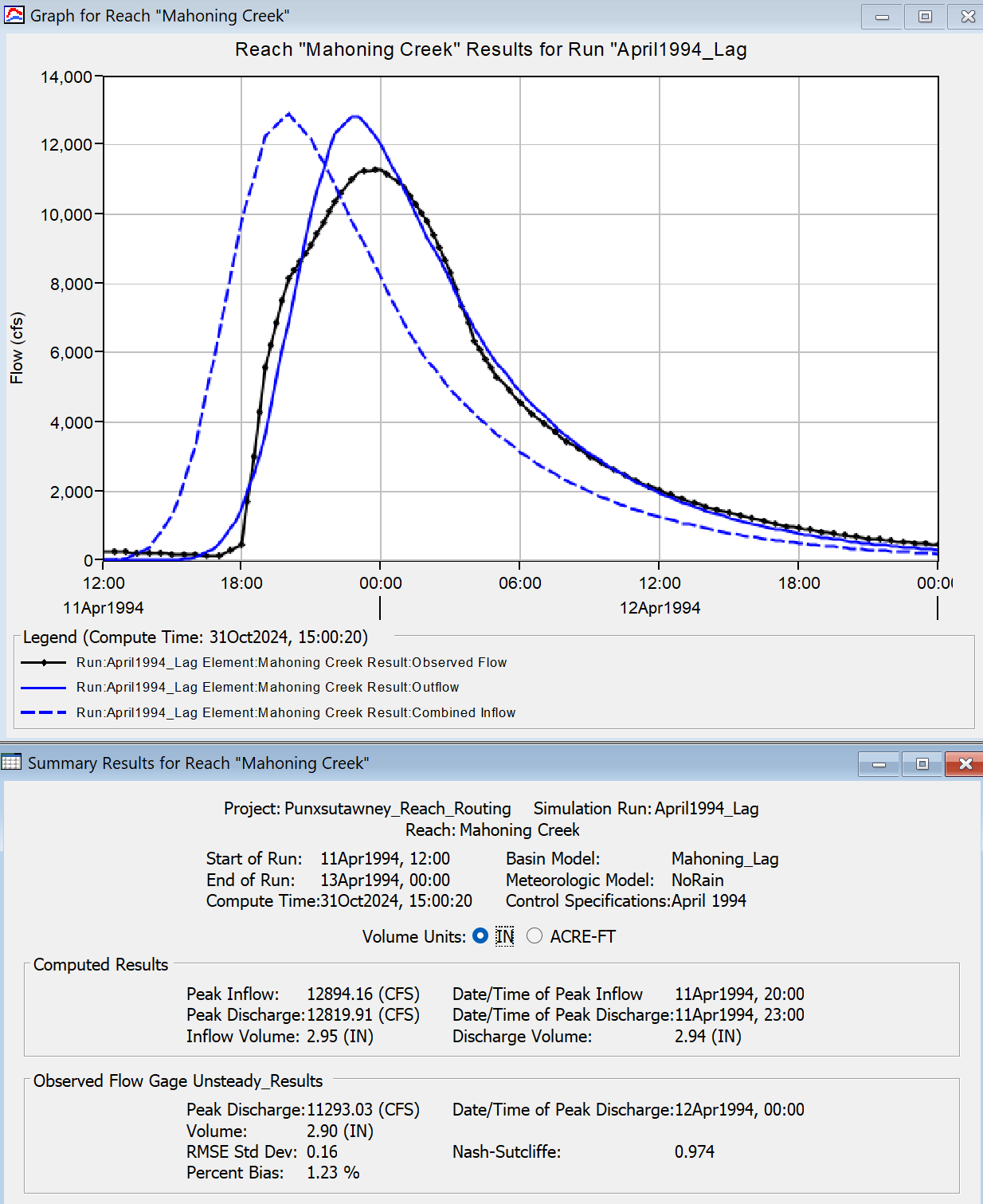
      Figure 4. Initial Results
    3. To better match the observed discharge, the Lag routing method parameters must be calibrated.

Calibrate the Model

Calibrating a model to afford better agreement between computed and observed runoff oftentimes requires simultaneous changes to more than just one process (e.g. calibrate both transform and routing reach parameters at the same time).  However, within this tutorial, only the Lag routing method parameters will be modified.

  1. Adjust the Lag routing method parameters in an attempt to simultaneously best match the peak discharge flow rate, time of peak discharge, hydrograph shape, and discharge volume.  Record the various differences between the computed and observed discharge hydrographs in addition to the RMSE Std Dev, Percent Bias, and Nash-Sutcliffe statistical metrics as you adjust model parameters.

Download the final project files here:

Lag_v4.12_finish.zip

Summary Questions

Question 7. What were the final Lag routing parameters and corresponding computed discharge peak flow rate, time of peak, and volume (in ac-ft) for the calibrated model?  How do these values compare to the corresponding observed discharge values?

Using a lag time of 165 minutes results in a difference of approximately 1600 cfs, 75 minutes, and 141 ac-ft when comparing the peak flow rate, time of peak, and volume of the computed and observed discharge hydrographs, respectively.  Also, these parameters result in an RMSE Std Dev, Percent Bias, and Nash-Sutcliffe statistical metrics of 0.2, 1.26%, and 0.974, respectively, as shown in Figure 5.  However, these are by no means the only parameter combinations that can result in acceptable model calibration.

Figure 5. Final Results


Question 8. Is it possible to reduce the computed discharge hydrograph peak flow rate when using the Lag routing reach method?  If not, why?

No.  When using the Lag routing reach method, only translation processes are simulated.  No attenuation or diffusion of the inflow hydrograph will be simulated.

Continue to Applying the Muskingum Routing Method