Implicit Finite Difference Scheme

The most successful and accepted procedure for solving the one-dimensional unsteady flow equations is the four-point implicit scheme, also known as the box scheme (see figure below). Under this scheme, space derivatives and function values are evaluated at an interior point, $//<![CDATA[ \begin{array}{l}(n+\theta) \Delta t\end{array} //]]>$. Thus values at $//<![CDATA[ \begin{array}{l}(n+1) \Delta t\end{array} //]]>$ enter into all terms in the equations. For a reach of river, a system of simultaneous equations results. The simultaneous solution is an important aspect of this scheme because it allows information from the entire reach to influence the solution at any one point. Consequently, the time step can be significantly larger than with explicit numerical schemes. Von Neumann stability analyses performed by Fread (1974), and Liggett and Cunge (1975), show the implicit scheme to be unconditionally stable (theoretically) for 0.5 < $//<![CDATA[ \begin{array}{l}\theta\end{array} //]]>$ ≤ 1.0, conditionally stable for $//<![CDATA[ \begin{array}{l}\theta\end{array} //]]>$ = 0.5, and unstable for $//<![CDATA[ \begin{array}{l}\theta\end{array} //]]>$ < 0.5. In a convergence analysis performed by the same authors, it was shown that numerical damping increased as the ratio $//<![CDATA[ \begin{array}{l}\lambda / \Delta x\end{array} //]]>$ decreased, where $//<![CDATA[ \begin{array}{l}\lambda\end{array} //]]>$ is the length of a wave in the hydraulic system. For streamflow routing problems where the wavelengths are long with respect to spatial distances, convergence is not a serious problem.

In practice, other factors may also contribute to the non-stability of the solution scheme. These factors include dramatic changes in channel cross-sectional properties, abrupt changes in channel slope, characteristics of the flood wave itself, and complex hydraulic structures such as levees, bridges, culverts, weirs, and spillways. In fact, these other factors often overwhelm any stability considerations associated with $//<![CDATA[ \begin{array}{l}\theta\end{array} //]]>$. Because of these factors, any model application should be accompanied by a sensitivity study, where the accuracy and the stability of the solution are tested with various time and distance intervals.

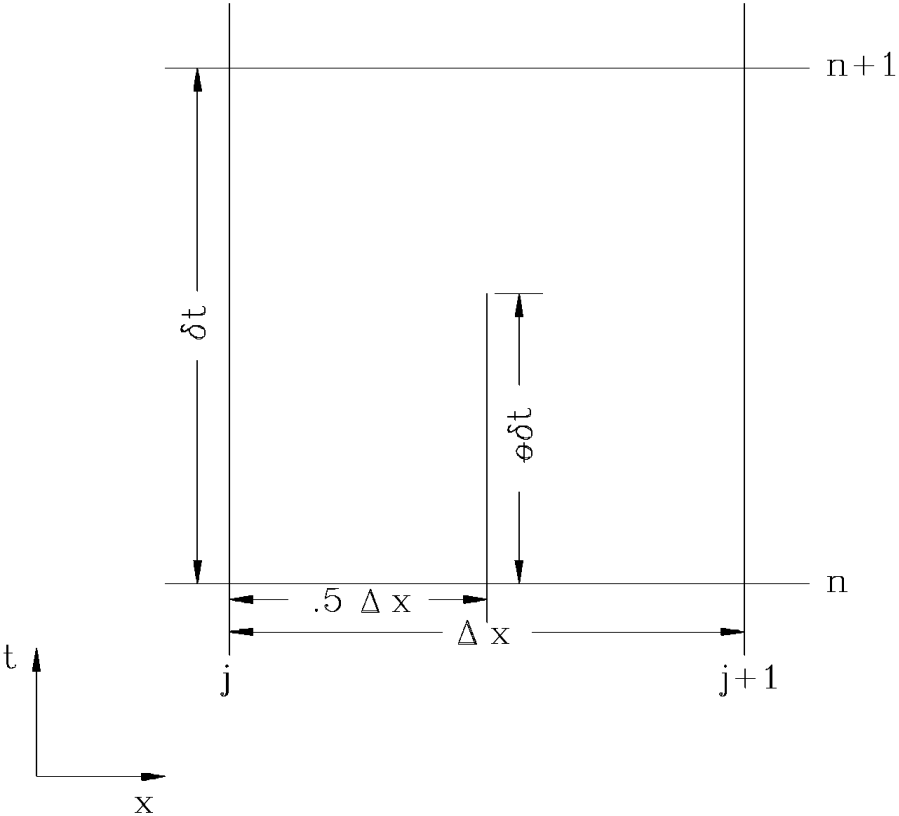
The following notation is defined:

and:

then:

The general implicit finite difference forms are:

1. Time derivative

   4)	$$//<![CDATA[ \begin{array}{l}\displaystyle \displaystyle \frac{\partial f}{\partial t} \approx \frac{\Delta f}{\Delta t} = \frac{\Delta f_{j+1} + \Delta f_j}{2 \Delta t}\end{array} //]]>$$

2. Space derivative

   5)	$$//<![CDATA[ \begin{array}{l}\displaystyle \displaystyle \frac{\partial f}{\partial x} \approx \frac{\Delta f}{\Delta x} = \frac{\left( f_{j+1} - f_j \right) + \theta \left( \Delta f_{j+1} - \Delta f_j \right)}{\Delta x}\end{array} //]]>$$

3. Function value

   6)	$$//<![CDATA[ \begin{array}{l}\displaystyle \displaystyle f \approx \overline{f} = 0.5 (f_j + f_{j+1}) + 0.5 \theta (\Delta f_j + \Delta f_{j+1} )\end{array} //]]>$$