Water Quality Transport Numerical Methods

River Reaches

The advection-dispersion-reaction equation is solved using an explicit, finite-volume method on a discretized version of the watershed geometry described in Computational Geometry. For river reaches, the finite volume cells consist of longitudinal sections of the river. The interfaces between adjacent computational cells are referred to as cell "faces".

Hydrodynamic variables (flows, velocities, surface areas, etc.) are computed in HEC-ResSim and passed to the WQ Engine (see HEC-ResSim Hydrologic Computations). Cell concentrations ( $\begin{array}{l}C\end{array}$ ) and volumes ( $\begin{array}{l}V\end{array}$ ) are defined at the cell locations, and velocities ( $\begin{array}{l}v\end{array}$ ), flows ( $\begin{array}{l}Q\end{array}$ ), conveyance areas ( $\begin{array}{l}A\end{array}$ ), and diffusion coefficients ( $\begin{array}{l}K\end{array}$ ) are defined at the face locations.

To derive the finite volume approach, the advection-diffusion-reaction equation is first integrated over the computational cell (control volume).

$\begin{array}{l}\displaystyle \int_V \frac{\partial C}{\partial t} dV + \int_V \frac{\partial (v C)}{\partial x} dV = \int_V \frac{\partial }{\partial x} \left( K \frac{\partial C}{\partial x} \right) dV + \int_V S dV\end{array}$

The advective and diffusive flux terms are then converted to surface integrals by applying the divergence theorem.

$\begin{array}{l}\displaystyle \frac{d}{dt} \int_V C dV + \oint_A v C dA = \oint_A K \frac{\partial C}{\partial x} dA + \int_V S dV\end{array}$

This equation is then applied to a generalized computational grid cell ( $\begin{array}{l}i\end{array}$ ) having a downstream face $\begin{array}{l}j\end{array}$ and an upstream face $\begin{array}{l}j-1\end{array}$ .

$\begin{array}{l}\displaystyle \frac{d}{dt} C_i V_i + \left( F_j - F_{j-1} \right) = \left( G_j - G_{j-1} \right) + S_i V_i\end{array}$

where $\begin{array}{l}F_j\end{array}$ are the advective fluxes at the faces and $\begin{array}{l}G_j\end{array}$ are the diffusive fluxes. These are calculated as:

$\begin{array}{l}\displaystyle F_j = v_j A_j C_j \hspace{1cm} G_j = K_j A_j \frac{C_{i+1} - C_i}{\Delta x_j}\end{array}$

$\begin{array}{l}A_j\end{array}$ is the cross-sectional area of flow at the face, and $\begin{array}{l}\Delta x_j\end{array}$ is distance between cell centers.

In the advective flux computation, the concentrations at the cell faces ( $\begin{array}{l}C_j\end{array}$ ) can be interpolated from the cell concentrations using a first order upwind method:

$\begin{array}{l}C_j = \begin{cases} C_i & \textrm{if } v_j \ge 0 \\ C_{i+1} & \textrm{otherwise} \end{cases}\end{array}$

The upwind method is stable, but introduces artificial diffusion, where gradients in water quality concentrations are spread out during transport because of the numerical approximation. Second order transport methods reduce numerical diffusion, but may cause oscillations around sharp concentration gradients. One solution is the use of flux limiters, where the face interpolation method is split into a first order and second order approximation terms. The use of the second order terms is controlled by a flux limiter, which applies them in areas where concentration gradients are relatively smooth, and does not apply them near sharp gradients. The resulting method is stable and almost second order accurate.

$\begin{array}{l}C_j = \begin{cases} C_i + \frac{1}{2} \phi(r_i) (C_i - C_{i-1}) & \textrm{if } v_j \ge 0 \\ C_{i+1} + \frac{1}{2} \phi(r_{i+1}) (C_{i+2} - C_{i+1}) & \textrm{otherwise} \end{cases}\end{array}$

where

$\begin{array}{l}\phi\end{array}$ is the flux limiter function, and
$\begin{array}{l}r_i = (C_i - C_{i-1}) / (C_{i+1} - C_i)\end{array}$ is a measure of the local smoothness.

Several flux limiter functions are available (Durran, 1999):

$\begin{array}{ll} \phi(r) = \max[0, \min(1, r)] & \textrm{Minmod} \\ \phi(r) = \max[0, \min(1, 2r), \min(2, r)] & \textrm{Superbee} \\ \phi(r) = (r + |r|) / (1 + |r|) & \textrm{Van Leer} \\ \phi(r) = \max \left[0, \min(2, \frac{1+r}{2}, 2r) \right] & \textrm{Monotonized Centered (MC)} \end{array}$

Following testing on transport through ResSim reaches, the van Leer limiter was chosen for use in the WQ Engine. Because of the staggered grid setup, the central differencing used by the diffusive flux approximation is second order accurate without the need for flux limiters.

The time derivative is discretized using explicit Euler

$\begin{array}{l}\displaystyle \frac{d}{dt} C = \frac{C^{n+1} - C^n}{\Delta t}\end{array}$

where the superscript $\begin{array}{l}n\end{array}$ denotes values at the beginning of the time step, $\begin{array}{l}n+1\end{array}$ denotes values at the end of the time step, and $\begin{array}{l}\Delta t\end{array}$ is the user-defined time step length (e.g., 1 hour).

The full discretized transport equation for updating cell concentrations can then be written

1)	$\begin{array}{l}\displaystyle C^{n+1}_i V^{n+1}_i = C^n_i \, V^n_i + \Delta t \left[ (G_j^n - G^n_{j-1}) - (F^n_j - F^n_{j-1}) \right] + \Delta t \, S^n_i \, V^n_i\end{array}$

Cell volumes at the end of the time step are calculated using conservation of volume:

$\begin{array}{l}\displaystyle V^{n+1}_i = V^n_i + \Delta t \left( Q_j^{n+1/2} - Q_{j-1}^{n+1/2} \right)\end{array}$

where the time step $\begin{array}{l}n+1/2\end{array}$ is used to indicate the average flow into and out of the cell over the time step.

Time Step Limitations

The explicit numerical solution is subject to restrictions on the length of the time step to ensure stability. These restrictions are easiest to understand for the advection term, and derive from the requirement that the upwind concentration must be the concentration in the cell immediately upstream (and not the concentration in a cell farther upstream). The time step must therefore be short enough that material does not move farther than the length of one cell.

$\begin{array}{l}\displaystyle v\, \Delta t < \Delta x \quad \rightarrow \quad \frac{v\, \Delta t }{\Delta x } \le 1\end{array}$

This condition is called the Courant (or CFL) condition. For the full, discretized advection-diffusion-reaction equation, the stability condition is more restrictive (see Durran, 1999 for derivation details)

$\begin{array}{l}\displaystyle 0 \le \frac{v\, \Delta t }{\Delta x } + \frac{K \Delta t }{(\Delta x )^2} + \frac{k \Delta t}{2} \le 1\end{array}$

In the above equation, the source-sink is formulated as an aggregated, first order reaction term $\begin{array}{l}S = -k C\end{array}$ with a rate coefficient $\begin{array}{l}k\end{array}$ . In general, higher velocities, higher dispersion rates, and faster reaction rates require smaller time steps.

To avoid violating the stability condition, the maximum allowable time step is computed at the start of every computational step based on that step's velocities, dispersion coefficients, and reaction rates. The smallest computed maximum time step over all the cells in the reach ( $\begin{array}{l}\Delta t_{\textrm{limit}}\end{array}$ ) is found. That value is used to determine the integer number of sub-time steps for which Equation 1) will be applied.

$\begin{array}{l}\displaystyle N_{\textrm{substeps}} = \left\lceil \frac{\Delta t}{\Delta t_{\textrm{limit}}} \right\rceil\end{array}$

For example, if a user-defined time step of 1 hour is used, but $\begin{array}{l}\Delta t_{\textrm{limit}}\end{array}$ is 14.2 minutes, then five sub-time steps will be used to compute the hour. Each of the five steps will have $\begin{array}{l}\Delta t_{\textrm{substep}}\end{array}$ = 12 minutes. Because velocities, dispersion coefficients, and reaction rates vary throughout the simulation, the number of sub-time steps must be computed again at the start of the next hourly time step.

Reservoirs

For reservoirs, the finite volume cells consist of slices of the reservoir volume, with layer interfaces at fixed elevations.

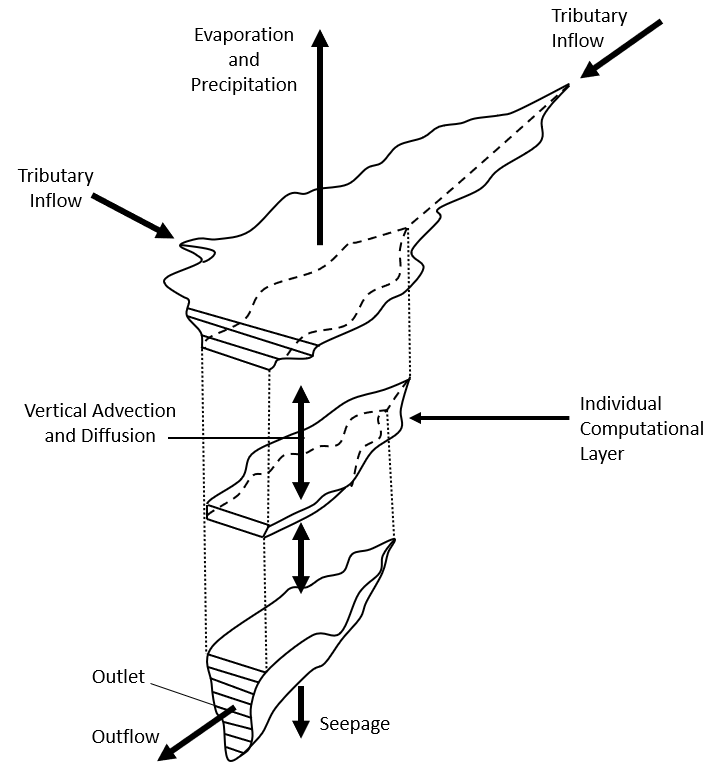
The numerical solution to the transport equation in reservoirs is the same as described for reaches. The surface areas of the layer interfaces are used in place of conveyance areas, and the system is much less driven by advection, with vertical velocities often orders of magnitude smaller than longitudinal river velocities. The main difference in the HEC-WQ Engine is that, instead of velocities and flows passed in at the cell faces by the HEC-ResSim program, the rates for evaporation, precipitation, seepage, and all inflows and outflows are passed in, and the WQ Engine calculates the vertical velocities at the layer interfaces. The reason for this is that the WQ Engine must first calculate the distribution of inflows and outflows to individual reservoir layers. This is done based on the current state of the reservoir stratification, the boundary flow magnitude, and the boundary flow density (for inflows) (see Reservoir Hydraulics section).

Once the inflows ( $\begin{array}{l}Q_i^{\textrm{in}}\end{array}$ ) and outflows ( $\begin{array}{l}Q_i^{\textrm{out}}\end{array}$ ) to each layer are calculated, the velocities between layers can be calculated by applying conservation of volume from the bottom to the top active layer. This is possible since only the top active layer changes volume within a time step.

for i in range(1, nTop-1):
    $\begin{array}{l}Q_j = \sum_k Q_i^{\textrm{in,}k} - \sum_k Q_i^{\textrm{out},k} + Q_{j-1}\end{array}$ 
    $\begin{array}{l}v_j = Q_j / A_j\end{array}$

where $\begin{array}{l}k\end{array}$ denotes the individual inflow or outflow. Seepage is applied to the bottom layer. The volume of the top active layer is updated based on flow from the layer below as well as any evaporation or precipitation. Layer interfaces are at fixed elevations, and do not expand or contract dynamically during the simulation. If the water level increases to wet a new layer within a time step, the water quality concentrations from the layer beneath are applied to the new top layer. If the top active water layer dries during a time step, the water quality concentrations from the previous and new active top layers are volume-averaged, to ensure conservation of mass.

Following the update of all cell concentrations for a time step, the vertical density profile is examined. If the density profile is not monotonically increasing from top to bottom of the reservoir (unstable stratification), layers are mixed downward (assuming conservation of mass) until a stable density profile is achieved. An unstable density profile may result from surface heat loss at night, for example. A stable density profile is an implicit assumption of the inflow and outflow computations described in the Reservoir Inflow and Reservoir Outflow sections.